是,应该准确来说是相对同一个分布以及同一个模型
你输出l就会发现他是一个二维张量,但是l.backward()默认参数是一维的。你可以给个二位张量作为参数,参数就是和l一样大小的一样维度的张量,比如l.backward(torch.ones_like(l))
animator = d2l.Animator(xlabel='order of poly', ylabel='loss', yscale='log',
xlim=[1, 20], ylim=[1e-3, 1e2],
legend=['train', 'test'])
for i in range(2,21):
train_loss, val_loss = train(poly_features[:n_train, :i], poly_features[n_train:, :i],
labels[:n_train], labels[n_train:], num_epochs=1500)
animator.add(i, (train_loss,val_loss))
把train改一下,返回最后的训练误差和验证误差,然后再通过控制阶数去训练,画图
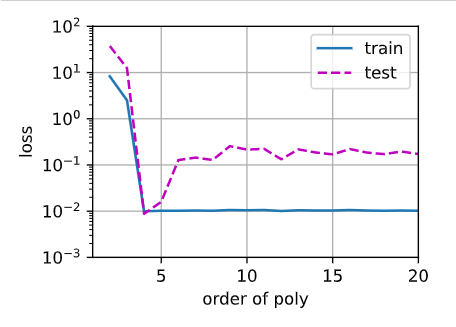
控制阶数2~20,训练误差和验证误差的关系如下:
应该是features值都太小了
在features等于零附近,高阶项的影响比较小
改成:features = np.random.normal(scale=1.5,size=(n_train + n_test, 1))
根据图像可以看出,当多项式特征取前四个维度时,损失最小,但此时仍未达到0。在图像左侧,训练损失远远大于测试损失,体现了欠拟合,右侧则表现出测试损失始终大于训练损失,体现了过拟合。
# 训练函数
def train_parameter(train_features, test_features, train_labels, test_labels, num_epochs=400):
loss = nn.MSELoss(reduction='none')
input_shape = train_features.shape[-1]
# 不设置偏置,在多项式里已经实现
net = nn.Sequential(nn.Linear(input_shape, 1, bias=False))
batch_size = min(10, train_labels.shape[0])
# print(train_features.shape, train_labels.shape)
train_iter = d2l.load_array((train_features, train_labels.reshape(-1, 1)),
batch_size) # (100, 4) (100, 1)
test_iter = d2l.load_array((test_features, test_labels.reshape(-1, 1)),
batch_size, is_train=False)
trainer = torch.optim.SGD(net.parameters(), lr=0.01)
for epoch in range(num_epochs):
d2l.train_epoch_ch3(net, train_iter, loss, trainer)
return evaluate_loss(net, train_iter, loss), evaluate_loss(net, test_iter, loss)
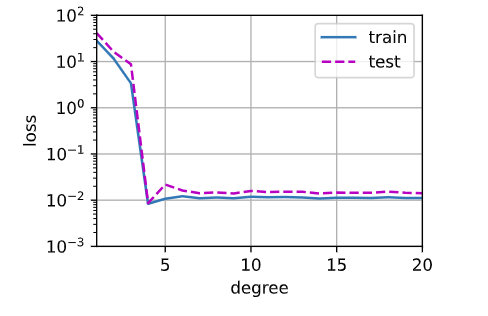
animator = d2l.Animator(xlabel='degree', ylabel='loss', yscale='log',
xlim=[1, max_degree], ylim=[1e-3, 1e2], legend=['train', 'test'])
for degree in range(max_degree):
loss_train, loss_test = train_parameter(poly_features[:n_train, :(degree+1)], poly_features[n_train:, :(degree+1)],
labels[:n_train], labels[n_train:])
animator.add(degree+1, (loss_train, loss_test))
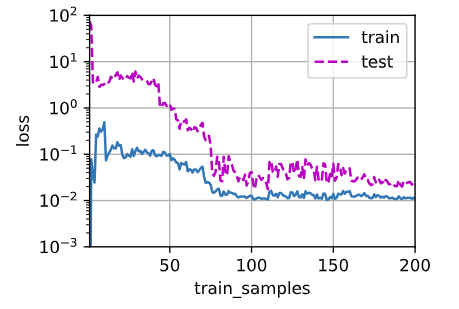
下图为多项式特征取前四个维度,测试样本数量为100,训练样本数量逐步从1增加至200(共300个样本),相应的训练测试损失的图像。可以看出,模型泛化能力基本上随着训练样本数的增加而提高
animator = d2l.Animator(xlabel='train_samples', ylabel='loss', yscale='log',
xlim=[1, 200], ylim=[1e-3, 1e2], legend=['train', 'test'])
for num in range(200):
loss_train, loss_test = train_parameter(poly_features[:(num+1), :5], poly_features[n_train:, :5],
labels[:(num+1)], labels[n_train:])
animator.add(num+1, (loss_train, loss_test))
当我把训练样本和测试样本都调到很大时(1000),loss并没有太大降低,所以我比较怀疑训练样本是否会实质性提高模型泛化能力
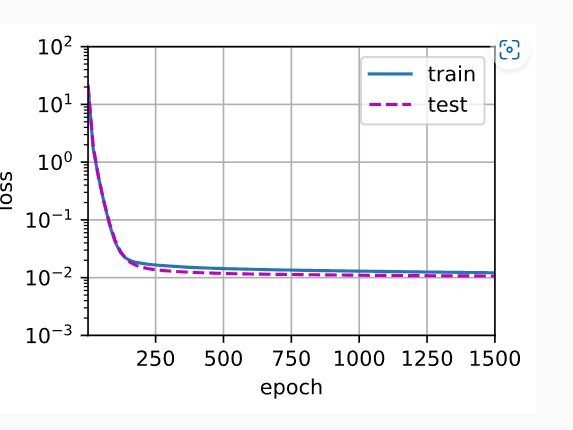
为什么这张图就能看出来过拟合,和之前那个拟合正常的有什么不同吗
为什么说,模型参数取值范围越大,越容易过拟合
loss = nn.MSELoss(reduction='none')改成 loss = nn.MSELoss(),这样loss是标量就可以求梯度了我觉得在上面例子中的模型并不是一个多项式模型,这个模型的本质还是一个单连接层的模型,模型的形状为(多项式的项数,1),只不过多项式的每一项变成了x1、x2、x3、x4、…,所以该模型还是y = w1+w2x1+w3x2+w4*x3+…
如果有理解不对的地方,欢迎各位大佬批判!Orz
你认为线性回归的解析解跟多项式回归的解析解是一样的?
module ‘d2l.torch’ has no attribute ‘train_epochs_ch3’. d2l库里没有这个函数呀
这是对的吧
一开始非常大
到 4个参数的时候 达到最佳
之后就发生了过拟合
[注] : module ‘d2l.torch’ has no attribute ‘train_epochs_ch3’ 可能开发人员把 ch3 章节代码删了
解决办法:
import d2l
print(d2l._file_)
查出你的电脑里d2l的包的地址
然后进去 torch.py
把 之前 softmax的0开始实现里的 train_epoch_ch3 和 train_ch3 复制粘贴进去,然后就可以了
-
这个多项式回归问题可以准确地解出吗?提示:使用线性代数。
答:不怎么会 ,线性代数可以解决 多维度问题么?
-
代码如下:
- 随着feature_num的增加 loss的变化
# 随着feature_num的增加 loss的变化
def train1(train_features,test_features,train_labels,
test_labels,num_epochs= 400):
loss = nn.MSELoss(reduction='none')
input_shape = train_features.shape[-1]
net = nn.Sequential(nn.Linear(input_shape,1,bias=False))
batch_size = min(10,train_labels.shape[0])
train_iter = d2l.load_array((train_features,
train_labels.reshape(-1,1)),batch_size)
test_iter = d2l.load_array((test_features,
test_labels.reshape(-1,1)),batch_size,is_train=False)
trainer = torch.optim.SGD(net.parameters(),lr=0.01)
for epoch in range(num_epochs):
d2l.train_epoch_ch3(net, train_iter, loss, trainer)
if epoch == 399:
train_loss=evaluate_loss(net,train_iter,loss)
test_loss = evaluate_loss(net,test_iter,loss)
return train_loss,test_loss
import matplotlib.pyplot as plt
a = range(1,20)
animator = d2l.Animator(xlabel='feature_nums', ylabel='loss', yscale='log',
xlim=[1, 20], ylim=[1e-3, 1e2],
legend=['train', 'test'])
for i in a:
c=0
d=0
c,d=train1(poly_features[:n_train,:i],poly_features[n_train:,:i],
labels[:n_train],labels[n_train:])
animator.add(i,(c,d))
结果:
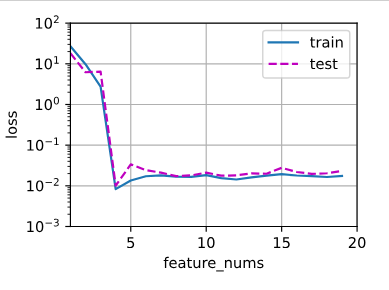
结论 : 随着 feature_nums 的增加模型的 loss 趋于稳定,虽然没有最低点nums=4效果好
但是 误差已经很小了,测试集和训练集相差结果也不是很大,过拟合可以接受
-
随着训练数据量的增加 loss的变化:
def train2(train_features,test_features,train_labels, test_labels,num_epochs=400): loss = nn.MSELoss(reduction='none') input_shape = train_features.shape[-1] net = nn.Sequential(nn.Linear(input_shape,1,bias=False)) batch_size = min(10,train_labels.shape[0]) train_iter = d2l.load_array((train_features, train_labels.reshape(-1,1)),batch_size) test_iter = d2l.load_array((test_features, test_labels.reshape(-1,1)),batch_size,is_train=False) trainer = torch.optim.SGD(net.parameters(),lr=0.01) for epoch in range(num_epochs): d2l.train_epoch_ch3(net, train_iter, loss, trainer) if epoch == (num_epochs-1): return evaluate_loss(net, train_iter, loss),evaluate_loss(net, test_iter, loss) b= range(1,n_train) anm = d2l.Animator(xlabel='data_nums',ylabel='loss',yscale='log', xlim=[1,n_train],ylim=[1e-3, 1e2], legend=['train','test']) for i in b: c=0 d=0 c,d = train2(poly_features[:i,:4],poly_features[n_train:,:4], labels[:i],labels[n_train:]) anm.add(i,(c,d))结果:
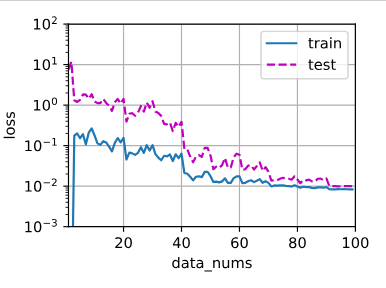
结论: 一开始明显过拟合 ,数据量太小 ,训练集误差小,测试集误差大
随着训练数据量的增加,训练集和测试集的loss 差距逐渐减小
80个epochs 后二者都趋于平稳
-
可能会发生上溢出 , 超过数据表示范围 ,而且数据太大也不利于计算
-
误差误差,泛化误差和训练误差都不可能为0(除非只有一个样本,训练误差为0)
为什么你这个相差这么多啊,我这个 几乎没差多少
emmmm,那这个问题本身就是这样算的嘛,按照线性回归的方式来进行计算,只是它多加了一个求幂的过程。
–>poly_features = np.power(features, np.arange(max_degree).reshape(1, -1))
多项式回归中的net = nn.Sequential(nn.Linear(input_shape, 1, bias=False))一句似乎创建了一个具有单一形状为(input_shape,1)的层,无偏置的网络。这是意在让这个网络去拟合阶数为input_shape的多项式吗?我不太明白这是怎么做到的。一个没有激活函数的,单一层的网络归根结底是一个线性函数,线性函数要怎么拟合一个3阶的多项式?
你可以算一下啊,就相当于求导,比如20多阶的导数求得次数多了,就变20!这种数了,超出计算机可以存储的最大数了
