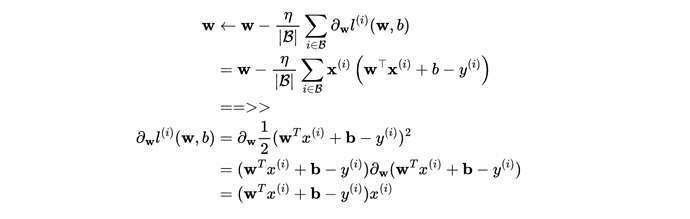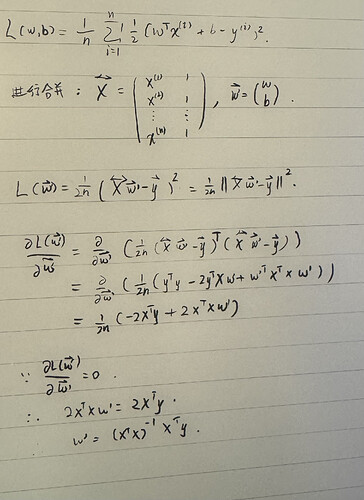台湾对于行和列的定义,与内地的定义(横为行,竖为列)是反的。
“在高斯噪声的假设下,最小化均方误差等价于对线性模型的极大似然估计。”
没有理解这个证明过程对于工作的意义是什么?通过将最小化均方误差问题与极大似然估计问题等效有什么意义?
对于3.1.13是怎么堆导的呢?
公式右边是噪声的概率密度函数
公式左边是已知y的情况下,求x,为什么等于右边呢?
求解析解可以利用符号函数去掉绝对值,再求导
噪声e(我用e表示噪声)服从正态分布,y = xw+b+e,那么e=y-xw-b也服从正态分布N~(0,sigma),代入正态分布公式里面就有了
第一题:题目求的是x = b + e, e服从正态分布下,b的极大似然估计。换句话说,题目假设了x是均值为b的正态分布
我在初次阅读时同样感到困惑,因为这与前文$y = w^Tx+b$中“向量默认为列向量”的表述相悖。当向量默认为列向量时,与您"行数代表样本的特征数量,列数代表样本数"的表述相吻合。
而当我阅读矩阵情况下的公式后,会发现y的计算公式发生了变化。此时$y=Xw+b$,X与w互换了位置,且w不再转置.在这一公式的前提下,文中的表述实质上是正确的。而如果将计算公式改为$y=w^TX+b$,则与您的表述重新吻合。
由x经过线性回归模型预测到的y的最大可能是噪声为高斯噪声的模型得到的预测结果。个人感觉似然翻译为可能性更好。
for epoch in range(num_epochs):
for X, y in data_iter(batch_size, features, labels):
l = loss(net(X, w, b), y) # X和y的小批量损失
# 因为l形状是(batch_size,1),而不是一个标量。l中的所有元素被加到一起,
# 并以此计算关于[w,b]的梯度
l.sum().backward()
sgd([w, b], lr, batch_size) # 使用参数的梯度更新参数
with torch.no_grad():
train_l = loss(net(features, w, b), labels)
print(f'epoch {epoch + 1}, loss {float(train_l.mean()):f}')
运行这段代码有如下报错:
RuntimeError: Trying to backward through the graph a second time (or directly access saved tensors after they have already been freed). Saved intermediate values of the graph are freed when you call .backward() or autograd.grad(). Specify retain_graph=True if you need to backward through the graph a second time or if you need to access saved tensors after calling backward.
我也添加了retain_graph=True还是同样的错误
我也觉得是
I agree with you
我觉着应该是他写错了,y=Xw+b,其中y,X,w分别是列向量,矩阵,列向量,后面加b利用广播机制。因此他们他们又可以表达为y=Xw+b,而b是一个列向量,每个元素为b,Xw+b=[X|b][w ;1] 这是大学线性代数中关于矩阵拆分成子矩阵的运算知识。由此可以看出,要合并矩阵,需要在 X后面插入一个b列向量,在w列向量下面加上一个标量1。这种扩充维度的方法以后将会在别的算法上频繁遇到的。
对于最大似然估计那一块,与其使用p(y|x)说明最大化似然可以取到最优w,b,不如使用L(w,b|y)可能更好解释:L代表参数为w和b的情况下y出现的可能性,而最大化L,就是找到最优的w和b,使得此时y出现的可能性最大
torch就是所谓的PyTorch框架本身,只是名字叫torch。
d2l是本书团队编写的包(就是你看到的@save那些函数的集合),但是包含不同框架对应可用的版本Mxnet/pytorch/tensorflow/paddle(各个版本里的函数及功能是一致的)。
from d2l import torch as d2l就是调用d2l包里的torch部分(跟torch框架本身是两回事),相当于import d2l.torch as d2l(别名);
如果你用tensorflow,那就是 import d2l.tensorflow as d2l(别名)
怎么好像说的都有点复杂,我的理解就是原先是样本只有一个x,所以就只有一个向量,但是样本很多变成数据集了,这个时候再用矩阵,因为矩阵乘法是行乘列,所以每一行相当于原来的一个样本,一列的全部就是特征
相当于简化了参数估计中的计算吧,因为效果是一样的。
2.4 应该是因为有的问题无法用凸优化方法解决,故采用梯度下降来求解。
这个比喻不合适,辟邪剑谱属于邪门歪道,因为“欲练此功,必先自宫”。
“import torch”:导入pytorch
“from d2l import torch as d2l”:导入pytorch版本的d2l,因为d2l基于不同的框架,有很多个版本(还有tensorflow版,paddle版,等等)