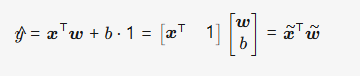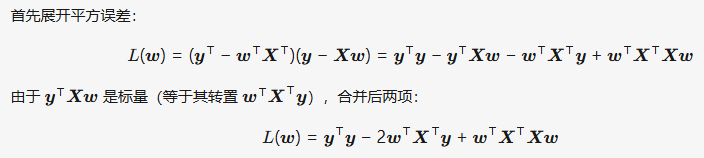解析解的话绝对值和的最小值与平方和最小值等价,如|x - 1|+|y - 2|和(x- 1)^2 + (y -2)^2有相同的最小值点,应该是这样
这是一条用于测试发帖的语句 //////////////////////////////
Q1:假设我们有一些数据x1, . . . , xn ∈ R。我们的目标是找到一个常数b,使得最小化∑ i(xi − b)2
A1:b大致是x的所有值的平均值,这正好是正态分布的均值。
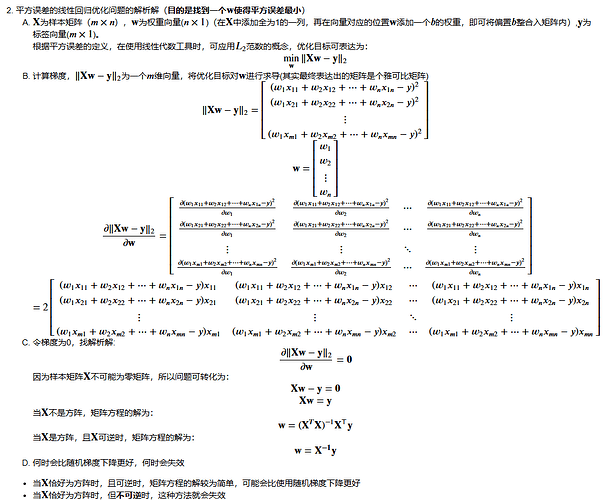
Q2:推导出使用平方误差的线性回归优化问题的解析解。为了简化问题,可以忽略偏置b(我们可以通过 向X添加所有值为1的一列来做到这一点)。
A2:
使用随机梯度下降(SGD)的情况: 在以下情况下,随机梯度下降(SGD)可能更加合适:
- 数据集非常大,求闭式解的计算量太大。直接计算 (XTX)−1(\mathbf{X}^T \mathbf{X})^{-1}(XTX)−1 可能不可行。
- 需要实时更新模型,SGD可以逐步更新权重,每次使用一个数据点来更新。
闭式解失效的情况: 闭式解可能失效或不可行的情况包括:
- 当 XTX\mathbf{X}^T \mathbf{X}XTX 不可逆时(例如,当特征之间高度相关,即多重共线性时)。
- 数据集过大时,矩阵求逆的计算量太高,导致计算不可行。
Q3:假定控制附加噪声ε的噪声模型是指数分布。
A3:
1.
2. 由于绝对值损失在 yi=xiTwy_i = \mathbf{x}_i^T \mathbf{w}yi=xiTw 处不可导,所以求出解析解较为复杂,一般没有简单的解析解。在实际应用中,绝对值损失的最小化通常使用迭代方法(如梯度下降)来近似求解,而不是通过解析方法得到解。
3. 在使用随机梯度下降法时,当我们不断更新参数时,可能会在驻点附近出现震荡。这是因为绝对值损失函数的梯度在误差接近零时会发生跳变,导致优化过程在接近最优解时不平稳。
为了避免驻点附近的震荡问题,我们可以采取以下方法:
- 学习率衰减:在优化过程中逐渐减小学习率,使得靠近最优解时步伐变小,从而减少震荡。
- 动量法:在每次更新时引入动量项,帮助权重更新更平滑。
- 使用替代损失函数:如 Huber 损失,它在误差较小时表现为平方损失,误差较大时表现为绝对值损失,从而兼具稳定性和平滑性。
2 Likes
我认为hyper parameter就是带有一些不可解释的部分,要看结果来反推超参数选择的怎么样
这是sphinx包的扩展标签,用于导出时生成章节标题和交叉引用的,只有在导出时才能自动转换。
感觉1.2应该是个开放题,首先想到了中心极限定理,如果n足够大,无论X服从什么分布,其均值都服从正态分布。
其次,可以把问题中的式子看做一维线性模型x=b(即用b估计x_i)的方差,类似二维模型,假设模型误差服从正态分布,x=b+误差,通过最大似然估计,同样可以求出最大似然估计,和最小化方差时解出来的b等价,也就是同样验证了:在高斯噪声的假设下,最小化均方误差等价于对线性模型的极大似然估计。即最小二乘法可以用于线性回归。
好工整!请问这种排版是哪什么软件做的呀?