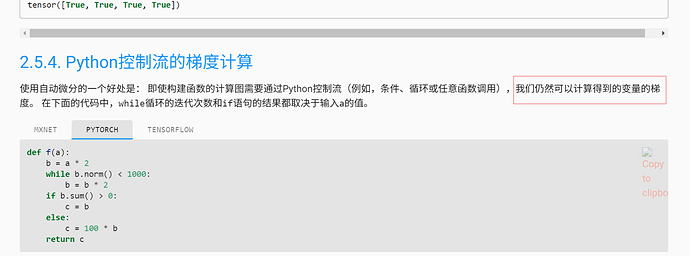
说一个语法的小问题,图片中的这句话是不是可以改为:我们仍然可以计算到变量的梯度
我也遇到这问题了。这误差也太大了吧… 小数点后两位
我觉得无论重复第一种测试多少遍,都无法提供新的有效信息,求出概率不变
其实应该是 向量z 的梯度上各个值求和,但根据微分的线性性质,梯度求和 和求和的梯度等价。这样转换一下,简单明了
维度为空代表其是一个标量,这句话在视频里面有涉及到
Continuing the discussion from 自动求导:
自动求导,把非标量变为标量,常用sum求一个批量和的方式,然后使用时在除以这个批量的个数得到真实的梯度。但发现,用sum求和后求梯度的结果,已经做了平均,然后在除以批量的个数是不是把梯度变小了?谢谢大家帮忙解惑
因为backward函数只能对标量的output求梯度,你可以自己演算一下,将y求和后再求梯度是不影响结果的
行列向量的定义只是帮助理解与人工演算,不应将其用于分析torch的代码输入与输出。在写代码时,对于一个tensor,你需要考虑的是它的shape
我的jupyter一用plot画图内核就挂了,啥情况啊?
请问一下为什么如果不使用detach的话会报错呢?
第五题
def my_sin_grad(x):
y = torch.sin(x).sum()
y.backward()
return x.grad
d2l.plot(x.detach().numpy(),[torch.sin(x).detach().numpy(),my_sin_grad(x).numpy()],‘x’,‘y’,legend=[‘f(x)’])
引号要改成英文引号,注意一下。。为什么代码块会有这个问题
-
为什么计算二阶导数比一阶导数的开销大?
答:二阶导数是一阶导数的导数,比一阶导数多计算一次导数,因此开销更大。 -
在运行反向传播函数后,立即再次运行,会发生什么?
答:会报错,在进行一次反向传播,计算图中的中间变量在计算完成后就释放了,之后无法再次计算反向传播。如果希望再次计算则需要将 retain_graph设置为True,也就是说保留计算图。 -
在控制流的例子中,计算d 关于a的导数,若将变量a改为随机向量或矩阵,会发生什么?
答:会报错,由于自动微分无法直接计算矩阵的梯度导致,要对矩阵做梯度,需要传入一个梯度参数(gradient),将其转换为标量,此时传入的梯度阐述需要匹配需要计算梯度的张量(梯度参数矩阵和求导的矩阵做点积,计算出一个标量)。 -
重新设计一个求控制流梯度的例子,运行并分析结果。
def z(a):
if a.sum() < 10:
return areturn 2 * a * a
x = torch.arange(5.0, requires_grad=True)
print(x)
y = z(x)
print(y)
y.sum().backward()
x.grad == 4 * x
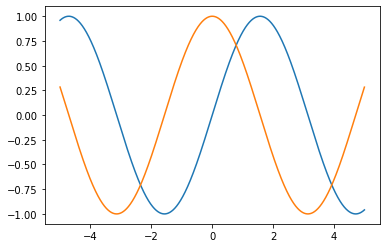
5.使 𝑓(𝑥)=𝑠𝑖𝑛(𝑥) ,绘制 𝑓(𝑥) 和 ∂𝑓(𝑥)/∂𝑥, 的图像,其中后者不使用 𝑓′(𝑥)=𝑐𝑜𝑠(𝑥)
import numpy as np
from matplotlib import pyplot as plt
def function(x):
return np.sin(x)
def derivative(func, x):
h = 1e-7
return (func(x + h) - func(x - h)) / (2 * h)
x = np.arange(-5, 5, 0.001)
y = function(x)
y_derivative = derivative(function, x)
plt.plot(x, y)
plt.plot(x, y_derivative)
plt.show()
以下是我问ChatGPT的答复:
其实在一些简单的情况下,我们是可以直接对y调用backward()函数的,不需要先对y进行求和。
例如,如果y是一个标量,那么我们可以直接对y调用backward()函数,例如:
y.backward()
这样可以计算得到y关于自变量的导数,并将结果累积到自变量的grad属性中。
但是,当y不是标量时,我们就需要先对y进行求和得到一个标量,然后再调用backward()函数。这是因为backward()函数只能计算标量关于自变量的导数,无法直接计算向量关于自变量的导数。
因此,在对一个向量或矩阵进行求导时,我们需要先对其进行某种操作(例如求和、平均值等)得到一个标量,然后再调用backward()函数计算导数。在本例中,我们对y进行了求和操作,得到一个标量,然后再调用backward()函数计算导数。
------------------------分割线---------------------------
个人理解,backward() 的计算逻辑必须需要一个标量,如果求导对象是向量或者矩阵,则:
- 要么提前通过sum()转换成标量
- 要么通过gradient参数来转换成标量
自动求导的输出必须是标量,所以求和目的是为了让非标量y变成标量,然后在计算图结构中去做y关于x的求导,求导后在计算图中free结构,就不可以在次backward了,除非加上retain_graph=True参数
you can reference code as below :q.reshape((1,12)) or q.reshape((12,1)),depend on your data shape of ‘q’.
question 5
a = nn.arange(0,4,0.1,requires_grad=True)
x1 = nn.sin(a)
y1 = x1.detach().numpy()
x1.sum().backward()
print(a.grad)
y2 = a.grad.detach().numpy()
x = a.detach().numpy()
plot(x, [y1, y2], ‘x’, ‘f(x)’, legend=[‘f = sin’, ’ f’ '],figsize=(500,500))
1.二阶导数是一阶导数的导数,会多加一个层次,开销肯定会更大一点
2. 不可以连续backward,会产生报错
3.d要先计算成为一个标量才能进行backward
4.略过
5.不显示使用cosx,可以使用自动求导方式
grad=torch.zeros_like(y)#创建保存f’(x[i]) 导数的向量grad
x1=x.detach().numpy()#tensor转array才可以调用绘图函数
y1=y.detach().numpy()
for i in range(len(grad)): #求sinx在每一个x[i]处的导数
y[i].backward(retain_graph=True) #隐式自动求导
grad[i]=x.grad[i]
grad.numpy()