第五问里面,对f(x)进行求导,也就是非标量求导。是不是要计算sum()然后再backward,这里有点不太理解,非标量调用backward()函数要输入的gradient参数的具体意义。请问应该怎么理解?
如果y是矩阵,要先把y转化为标量,再求导。转化为方法是:backward()函数传入一个矩阵m,计算y*m(y的各元素与m的元素对应相乘,不是矩阵相乘),再求矩阵元素之和,这样得到一个标量(实际就是y中的元素加权求和),然后才能求导
param -= lr * param.grad / batch_size
这里的param和param.grad能够相运算前提是两者的shape是一样的,那么无论f(x)是怎样的,x.grad和x是否都是shape相等,这是怎么保证的,因为从矩阵求导的定义无法理解,这与y.sum().backward()是否有关。求教
for Question 3:
in:
q = torch.randn(12, requires_grad = True)
q = q.reshape(3,4)
q = q.reshape(-1)
q
out:
tensor([ 1.3042, 0.3852, 0.6637, -0.2910, -0.3754, 1.0289, -0.1927, 1.1448,
0.1405, 0.3172, 0.9279, -1.0135], grad_fn<ViewBackward>)
in:
q = torch.randn(12, requires_grad = True)
q
out:
tensor([-0.9473, 0.5324, 1.6836, -1.2992, -0.1797, -1.2123, -1.9295, 1.2117,
0.4447, -0.3603, 0.5218, 0.3830], requires_grad=True)
I am wondering how to understand “reshape” in the above case. What I can do if I want to change my tensor back to be a leaf tensor after “reshape”?
import torch
import matplotlib.pyplot as plt
%matplotlib inline
x = torch.arange(0.0,10.0,0.1)
x.requires_grad_(True)
x1 = x.detach()
y1 = torch.sin(x1)
y2 = torch.sin(x)
y2.sum().backward()
plt.plot(x1,y1)
plt.plot(x1,x.grad)
练习五
import sys
sys.path.append(’…’)
from d2l import torch as d2l
x=torch.arange(0.,10.,0.1)
x.requires_grad_(True)
y=torch.sin(x)
y.sum().backward()
d2l.plot(x.detach(),[y.detach(),x.grad],‘x’,‘y’,legend=[‘y’,‘dy/dx’])
Question1:
- 计算二阶导数是在一阶导数的基础上进行的,自然开销要大。
https://baike.baidu.com/item/%E4%BA%8C%E9%98%B6%E5%AF%BC%E6%95%B0#:~:text=%E4%BA%8C%E9%98%B6%E5%AF%BC%E6%95%B0%E6%98%AF%E4%B8%80,%E5%87%BD%E6%95%B0%E5%9B%BE%E5%83%8F%E7%9A%84%E5%87%B9%E5%87%B8%E6%80%A7%E3%80%82
[4]
Question2:
import torch
x = torch.arange(40.,requires_grad=True)
y = 2 * torch.dot(x**2,torch.ones_like(x))
y.backward()
x.grad
y.backward() <======== If run backward the second time we will have run time error as below
RuntimeError: Trying to backward through the graph a second time, but the saved intermediate results have already been freed. Specify retain_graph=True when calling .backward() or autograd.grad() the first time.
If we use y.backward(retain_graph=True) then we can run y.backward() again as it will do one more time the computation graph
Question3:
def f(a):
b = a * 2
while b.norm() < 1000:
print(“\n”,b.norm())
b = b * 2
if b.sum() > 0:
c = b
print(“C==b\n”,c)
else:
c = 100 * b
print(“c=100b\n”,c)
return ca = torch.randn(size=(3,1), requires_grad=True)
print(a.shape)
print(a)
d = f(a)
d.backward() #<====== run time error if a is vector or matrix RuntimeError: grad can be implicitly created only for scalar outputs
d.sum().backward() #<===== this way it will work
print(d)
Question4:
def f(a):
b=a2+abs(a)
c=b3-b**(-4)
return c
a = torch.randn(size=(3,1), requires_grad=True)
print(a.shape)
print(a)
d = f(a)
d.sum().backward()
print(a.grad)
Question5:
%matplotlib inline
import matplotlib.pylab as plt
from matplotlib.ticker import FuncFormatter, MultipleLocator
import numpy as np
import torchf,ax=plt.subplots(1)
x = np.linspace(-3np.pi, 3np.pi, 100)
x1= torch.tensor(x, requires_grad=True)
y1= torch.sin(x1)
y1.sum().backward()ax.plot(x,np.sin(x),label=‘sin(x)’)
ax.plot(x,x1.grad,label=“gradient of sin(x)”)
ax.legend(loc=‘upper center’, shadow=True)ax.xaxis.set_major_formatter(FuncFormatter(
lambda val,pos: ‘{:.0g}$\pi$’.format(val/np.pi) if val !=0 else ‘0’
))
ax.xaxis.set_major_locator(MultipleLocator(base=np.pi))plt.show()
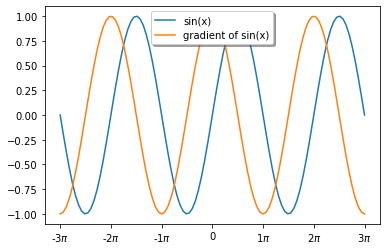
I got question below:
import torch
x = torch.randn(size=(3,6), requires_grad=True)
t = torch.randn(size=(3,6), requires_grad=True)
y = 2 * torch.dot(x,t)
y.backward()
x.grad
t.grad
I try to create a function of two variable x and t, then do y.backward, but why I got error:
1D tensors expected, but got 2D and 2D tensors
torch.dot() is a function for vector multiply vector, use torch.mm() for matrix multiply matrix
Thanks, it works
Extra question
import torch
x = torch.randn(size=(3,6), requires_grad=True)
t = torch.randn(size=(6,4), requires_grad=True)
y = 2 * torch.mm(x,t)
y.sum().backward()
x.grad
t.grad
tensor([[ 3.3685, 3.3685, 3.3685, 3.3685],
[-4.0740, -4.0740, -4.0740, -4.0740],
[ 5.9460, 5.9460, 5.9460, 5.9460],
[ 0.3694, 0.3694, 0.3694, 0.3694],
[-3.9745, -3.9745, -3.9745, -3.9745],
[-2.2524, -2.2524, -2.2524, -2.2524]])
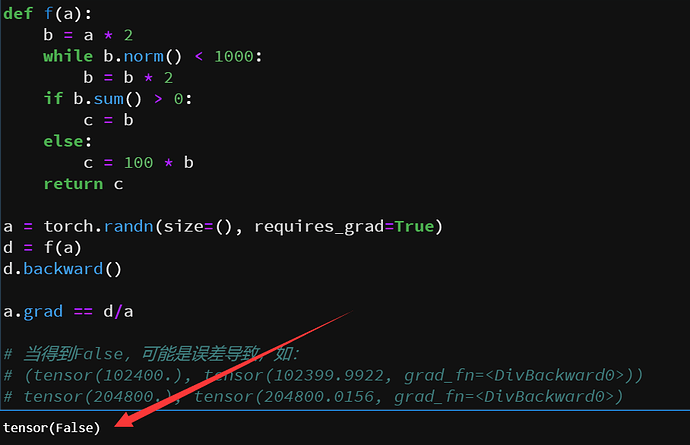
请问在2.5.4. Python控制流的梯度计算中
a = torch.randn(size=(), requires_grad=True)里面size()是什么意思呢?
size ( int… ) – a sequence of integers defining the shape of the output tensor. Can be a variable number of arguments or a collection like a list or tuple.
感谢回答,就是如果他是(3,4)我能明白他是想生成一个三行四列的矩阵,但是size=()不太明白是什么意思
size=()里面没有数是生成标量,有一个数就是向量,两个就是矩阵。
Thank you very much!!
import torch
import matplotlib.pyplot as plt
import numpy as np
x = torch.linspace(0, 3*np.pi, 128)
x.requires_grad_(True)
y = torch.sin(x) # y = sin(x)
y.sum().backward()
plt.plot(x.detach(), y.detach(), label='y=sin(x)')
plt.plot(x.detach(), x.grad, label='∂y/∂x=cos(x)') # dy/dx = cos(x)
plt.legend(loc='upper right')
plt.show()
Hi,
You got this error because the var x and y you created is 2D, and backward() expect a scalar input.
可以运行的,不过这里 post 的引号貌似都是中文的,需要自己改成英文引号