首先假设x是一个向量。f(x)对x求偏导数后,每个xi(向量x的分量)都会有自己的偏导数,所以x.grad和x的shape是相同的。如果x是矩阵结果也是一样的。
my solution for Question 5:
x = torch.linspace(-5, 5, 100)
x.requires_grad_(True)
y = torch.sin(x)
y.backward(torch.ones_like(x))
y = y.detach()
from utils import d2l
d2l.plot(x.detach(), [y, x.grad], 'f(x)', "f'(x)", legend=['f(x)', 'Tangent line'])
d2l.plt.show()
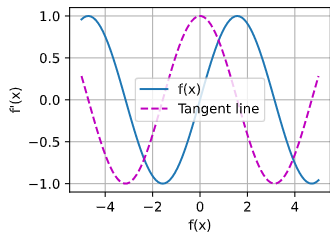
thanks. I run it successful
为什么按照PDF 上的 自动求导 y.backward().会报错。而且我也不理解为什么要求和再求导呢 y.sum().backward()
y 求和之后会是个数字。还怎么求梯度呢。不太理解什么意思。
import math
from d2l import torch as d2l
x=torch.arange(0,2*math.pi,0.01,requires_grad=True)
y=torch.sin(x)
y.backward(gradient=torch.ones(len(x)))
d2l.plot(x.detach(),[y.detach(),x.grad],‘x’,‘f(x)’,legend=[‘y’,‘df(x)/dx’])
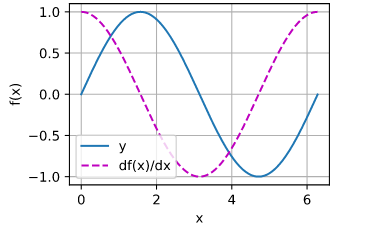
请问样例代码中:
x = torch.arange(4.0)
x
tensor([0., 1., 2., 3.])
求导之后
x.grad
tensor([ 0., 4., 8., 12.])
为什么从14张量求导后还是14,而不是4*1呢? 
for Q5:
# using plot function defined in 2.4
x = torch.arange(-2*torch.pi, torch.pi*2, 0.1,requires_grad=True)
f=torch.sin(x)
f.sum().backward()
f1=x.grad
x.requires_grad_(False)
plot(x, [torch.sin(x), f1], 'x', 'f(x)', legend=['f(x)=sin(x)', "f'(x)=cos(x)"])
关于自动求梯度函数 backward 的使用,这里有一个不错的讲解。
#5
from d2l import torch as d2l
import torch
import math
def f(x):
return torch.cos(x)
def toArray(x):
return x.detach()
x_1 = torch.arange(-1*math.pi, math.pi, 0.01, requires_grad=True)
d = f(x_1)
d.sum().backward()
x_grad = x_1.grad
d2l.plot(toArray(x_1), [toArray(d), toArray(x_grad)], ‘x’, ‘f(x)’, legend=[‘cos(x)’, ‘sin(x)’])
https://zhuanlan.zhihu.com/p/83172023 这里的解释经过我的验证,应该是正确的。
简洁的讲:我们需要一个和len(x)等大小的权重信息,来指示pytorch进行合理的求导。
请问torch中行向量和列向量做内积后为什么不能进行反向求导?代码如下:
import torch
x = torch.arange(4.0, requires_grad=True).reshape(4,1)
y = torch.mm(x.T, x)
y.sum().backward()
x.grad
结果x.grad为None
我想区分行向量和列向量,从而与数学理解更匹配,不知道上面操作为什么不行?
这是一个比较基础但是与 pytorch 底层实现比较相关的问题。
运行你的代码,会报错:
大概意思就是说正在访问非叶张量的梯度,也就是说 x 不是自动求导过程中梯度最后汇总的叶张量。对于 pytorch 是如何自动求导,可以看看我在这里发的那篇知乎的专栏。
简单来说,什么是叶张量呢?你创建张量的第一步,就是一个叶张量,也就是:
torch.arange(4.0, requires_grad=True)
但是,
x = torch.arange(4.0, requires_grad=True).reshape(4,1)
反而并不是一个叶张量,它是对于叶张量的一个操作后的结果。
作为示例,我把你的代码修正了一下:
import torch
x = torch.arange(4.0, requires_grad=True)
x_1 = x.reshape(4,1)
y = torch.mm(x_1.T, x_1)
y.sum().backward()
x.grad
这个就能计算出你需要的梯度了
非常感谢您的回答,后面会继续拜读您的知乎文章!
另外我想补充一个问题,采用您的修改方法后可以求出x.grad,但如何求x.T的梯度?
@WWWM
首先,那篇知乎的专栏并不是我写的。而是我自己搞不明白的时候,忽然看到,觉得豁然开朗,认为可以推荐给跟我一样有困惑的人……
然后,关于你想求出 x.T 的梯度,说实话,我有点不太理解你的意思,你是指把 x.T 看成一个新的变量,然后单独计算它的梯度吗?
如果是这样,那解决方法很简单,建立一个新的变量,然后调用它的 retain_grad() 方法就可以了:
import torch
x = torch.arange(4.0, requires_grad=True)
x_1 = x.reshape(4,1)
x_1_T = x_1.T
x_1_T.retain_grad()
y = torch.mm(x_1_T, x_1)
y.sum().backward()
x.grad,x_1_T.grad
输出结果如下:
(tensor([0., 2., 4., 6.]), tensor([[0., 1., 2., 3.]]))
不知道这个符不符合你的要求
import torch
x = torch.arange(4.0, requires_grad=True)
m=xx
n=mx
torch.autograd.backward(n,grad_tensors=torch.ones(x.shape),retain_graph=True,create_graph=True)
torch.autograd.backward(x.grad,grad_tensors=torch.ones(x.shape),retain_graph=True,create_graph=True)
ERROR:Trying to backward through the graph a second time (or directly access saved tensors after they have already been freed). Saved intermediate values of the graph are freed when you call .backward() or autograd.grad(). Specify retain_graph=True if you need to backward through the graph a second time or if you need to access saved tensors after calling backward.
在尝试求解二阶导数时为什么会出现这种问题?
感谢您的回复!
我的意思其实就是想问这个:
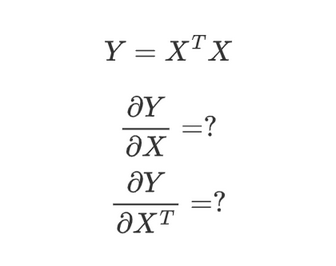
另外,对x.T求梯度为什么值变了?不应该只是和对x求梯度形状不同(或者相同)而已吗?
看完你的问题,我大致明白了你想要求什么,但是必须说的是,你显然没有理解pytorch自动求导的历程,在这里的 x_1 和 x_1_T 都不是最终的 x ,因此求导的结果并不是一致的。你可以理解成
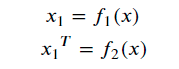
懂吗,新建立的两个变量 x_1 和 x_1_T 并不直接等同于一开始的 x ,它们相当于是根据 x 新创建的张量。