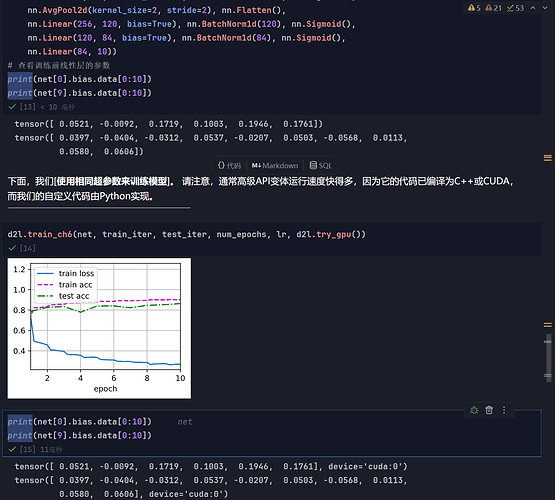
教程中使用BN后选择将学习率提高了,这是为什么呢?
我的一个猜想是:BN使得函数的值域变小,成为一个更小的区间,而自变量的范围不变,因此学习的步幅变大在值域上的移动并不会太多,但搜索次数可以变少,更便于找到最优解。是这样吗?
俺觉得有道理!紫薯布丁紫薯布丁紫薯布丁紫薯布丁
批量归一化的原理:
批量归一化的手动实现:
class BatchNorm(nn.Module):
def __init__(self, features: int, epsilon=1e-5, momentum=0.9):
"""
批量归一化层
通过每个小批量的均值 running_mean 和方差 running_var 归一化数据,并使用拉伸幅度 γ (gamma) 和偏移参数 β (beta) 学习并
恢复数据的分布特性。
:param features: 特征数。即,全连接层的特征数,或卷积层的通道数
:param epsilon: 小常数。保证在计算标准差时,方差不为零,避免除零错误
:param momentum: 动量系数。每个小批量的均值和方差更新时,依赖于历史统计量的程度,取值范围为 [0, 1]
"""
assert 0 <= momentum <= 1, '动量系数的取值范围为 [0, 1]'
super().__init__()
self.epsilon = epsilon
self.momentum = momentum
self.gamma = nn.Parameter(torch.ones(features)) # 注册可学习参数 gamma:拉伸幅度
self.beta = nn.Parameter(torch.zeros(features)) # 注册可学习参数 beta:偏移
self.register_buffer('running_mean', torch.zeros(features)) # 注册模型状态参数全局均值 running_mean 到缓冲区
self.register_buffer('running_var', torch.ones(features)) # 注册模型状态参数全局方差 running_var 到缓冲区
def forward(self, x: Tensor) -> Tensor:
"""根据输入数据的维度,进行批量归一化"""
if x.dim() == 2: # 输入数据来自全连接层的输出 (batch_size, features)
return self._batch_norm_fc(x)
elif x.dim() == 4: # 输入数据来自卷积层的输出 (batch_size, channels, height, width)
return self._batch_norm_conv(x)
else:
raise ValueError(f'暂不支持的输入形状:{x.shape}')
def _batch_norm_fc(self, x: Tensor) -> Tensor:
"""
对来自全连接层的输入进行批量归一化
计算各个特征的均值与方差(有偏估计,除以 n 而不是 n-1)
"""
if self.training:
mean = x.mean(dim=0, keepdim=True)
var = x.var(dim=0, keepdim=True, unbiased=False)
with torch.no_grad():
self.running_mean = (1 - self.momentum) * self.running_mean + self.momentum * mean
self.running_var = (1 - self.momentum) * self.running_var + self.momentum * var
else:
mean = self.running_mean
var = self.running_var
x_normalized = (x - mean) / torch.sqrt(var + self.epsilon)
out = self.gamma * x_normalized + self.beta
return out
def _batch_norm_conv(self, x: Tensor) -> Tensor:
"""
对来自卷积层的输入进行批量归一化
计算各个通道的均值与方差(有偏估计,除以 n 而不是 n-1)
"""
if self.training:
mean = x.mean(dim=(0, 2, 3), keepdim=True)
var = x.var(dim=(0, 2, 3), keepdim=True, unbiased=False)
with torch.no_grad():
self.running_mean = (1 - self.momentum) * self.running_mean + self.momentum * mean.squeeze()
self.running_var = (1 - self.momentum) * self.running_var + self.momentum * var.squeeze()
else:
mean = self.running_mean[None, :, None, None]
var = self.running_var[None, :, None, None]
x_normalized = (x - mean) / torch.sqrt(var + self.epsilon)
out = self.gamma[None, :, None, None] * x_normalized + self.beta[None, :, None, None]
return out
他这里面的讲解是这样的,但我觉得不太合理,我觉得应该精确平均到每一个特征点样本间的差距,应该是沿着batch维度来求均值。。我记得好像是andrew ng课里面还是哪里说的沿着batch维度做平均,得到CHW的形状
为什么训练的时候不用移动平均值来做BN啊,这样不是更符合整体分布吗??好奇怪。。
个人认为是模型每经过一轮训练,bn层的移动平均值和移动方差以及缩放偏差参数都会改变,而测试集未经过模型训练,这些参数不能完全代表测试集的特征分布,导致输出结果波动。
作业本
- 是可以删除或者禁用bias选项,反正因为后面都要进行正则化,所以bias选项就是冗余的
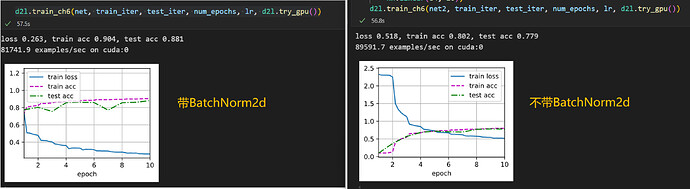
- LeNet正则化版本
net = nn.Sequential(
nn.Conv2d(1, 8, kernel_size=5, padding=2), nn.BatchNorm2d(8), nn.ReLU(),
nn.MaxPool2d(kernel_size=2, stride=2),
nn.Conv2d(8, 16, kernel_size=5), nn.BatchNorm2d(16), nn.ReLU(),
nn.MaxPool2d(kernel_size=2, stride=2),
nn.Flatten(),
nn.Linear(16 * 5 * 5, 120),nn.BatchNorm1d(120), nn.Sigmoid(),
nn.Linear(120, 84), nn.BatchNorm1d(84), nn.Sigmoid(),
nn.Linear(84, 10))
相比之下test_acc提高了不少哦
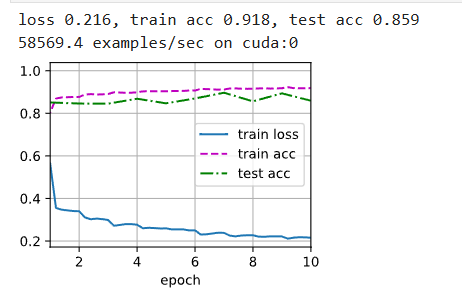
- 第四题
我觉得dropout方法是不可替换为batchNorm,一个用于避免某个节点过于重要和防止overfitting。但是BatchNorm主要用于加速收敛和防止过拟合
对比一下训练前后的偏置, 偏置根本没有被训练! 因为每个批次规范化后, b都被消掉了, b的梯度是0. 这表面b在训练时是完全可以删去的
而你运行后泛化水平下降, 我认为只是在测试时, 由于b为每层注入了随机数, 泛化能力提升. 其实应该可以在测试时随机生成b, 而不需要放入训练参数中, 就能达到同样的效果