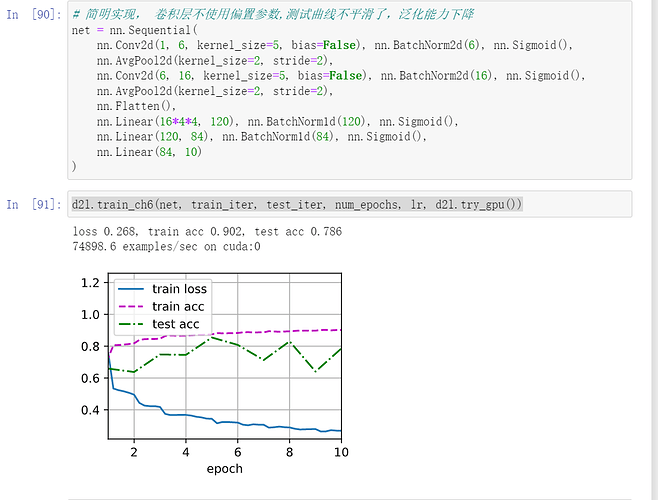
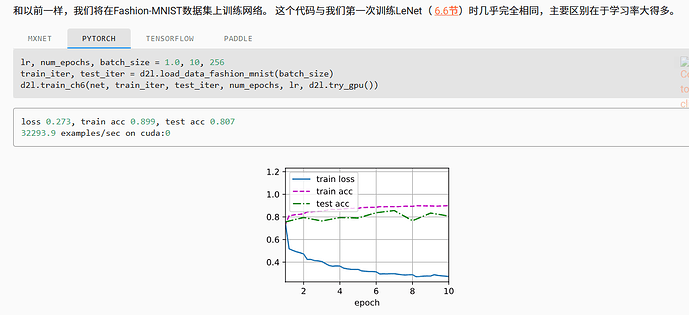
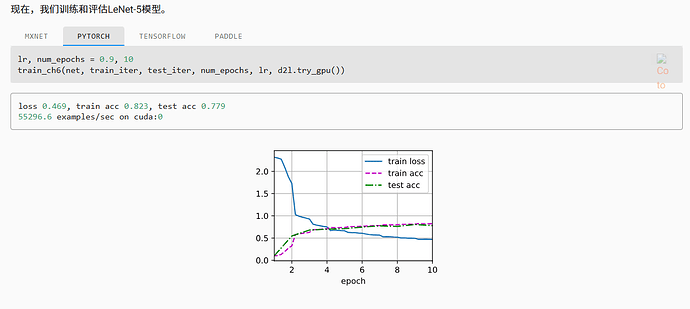
那对于卷积后面的BN呢,卷积是在C(channel)维上做的BN,batch=1也可以做啊?
因为学习率大,你把学习率调低就行了,再加上lenet是小模型,容易震荡
是的,你可以想到当batchsize等于1的时候,均值不就是这个数本身吗
我觉得可能保留后面两个维度是为了在后面的相减运算中使用python的广播特性
我有几个问题不解。
1.为什么gamma和beta分别被初始化为1矩阵和0矩阵,而不像其他权重那样优化成随机数矩阵?
2.momentum是个啥?看起来好像momentum表示的是进行批量规范化的一个批量跟总的样本数量之间的比值。但如果是这样的话,在从零开始的代码里面,momentum为什么可以是个确定值0.9呢?不是应该随着批量大小而变化吗?
我理解的是在每个输出通道上对小批量的所有样本求均值和方差,而不是对单个样本的所有输出通道求均值和方差,所以batch_size=1不能做
- 我的理解是最开始样本被归一化之后就是均值为0方差为1,这两个值是经验得来的比较靠谱?
- 可以搜索一下exponentially weighted moving average和RMSProp,这是一个超参数,通常被设为0.9
我认为是这样的。。。。。。。。。。。。。。。。。。。。。。。
在使用批量规范化之前,我们是否可以从全连接层或卷积层中删除偏置参数?为什么?
我认为是可以的,偏执最终也会被作为平均值中的一部分然后被减掉。
比较LeNet在使用和不使用批量规范化情况下的学习率
使用 :1.0 准确度 85.7%
不使用: 0.3 73.3%
我们是否需要在每个层中进行批量规范化?尝试一下?
只留了最后俩个batch-norm
lr:0.3 51.3% 测试集准确度大起大落不稳定
只留了前俩个batch-norm
lr:0.3 80.9% 测试集准确度较为稳定,说明相较于加在后面还是应该加在前面,可以确保数值稳定性。
你可以通过批量规范化来替换暂退法吗?行为会如何改变?
net = nn.Sequential(
nn.Conv2d(1, 6, kernel_size=5), nn.Sigmoid(),
nn.AvgPool2d(kernel_size=2, stride=2),
nn.Conv2d(6, 16, kernel_size=5), nn.Dropout(0.5), nn.Sigmoid(),
nn.AvgPool2d(kernel_size=2, stride=2), nn.Flatten(),
nn.Linear(256, 120), nn.Sigmoid(),
nn.Linear(120, 84), nn.Sigmoid(),
nn.Linear(84, 10))
lr:0.3 测试准确度 60.6%
到哪里去查看高级API中有关BatchNorm的在线文档?
请问指数平滑法,初始值应该为第一个batch的均值和方差,而这里初始为0和1,为什么?
optimizer,activation function, Pooling = adam, ReLU, avg
lr, num_epochs, batch_size = 0.001, 10, 64
epoch 8, loss 0.176, train acc 0.934, test acc 0.912
without BatchNorm1d
epoch 9, loss 0.188, train acc 0.930, test acc 0.911
也可以吧,毕竟batch为1,但是数据宽高不为1,还是有很多元素求平均,不至于减完平均变成0
主要也没用上这俩个东西啊,就return 了一个Y
关于全连接层输出的批量规范化,原文中是对每个输出,按照批量对应元素,规范化,比如10个样本数据,100个输出,第一个输出对应十个样本,他们规范化,其他的输出类似,在想为何不能按照每个样本去规范化,比如第一个样本的100个输出规范化,第二个。。依次类比,毕竟毕竟全连接层是每个样本的特征去决定某个输出的权重啊,不应该让他们作为一组去规范化么,毕竟他们才是一个整体要处理的信息。后来编程试了试,效果如下
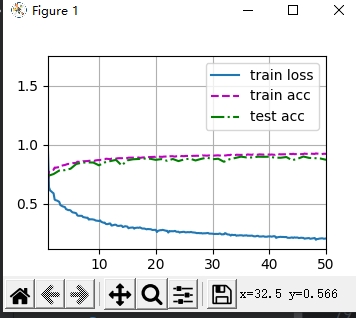
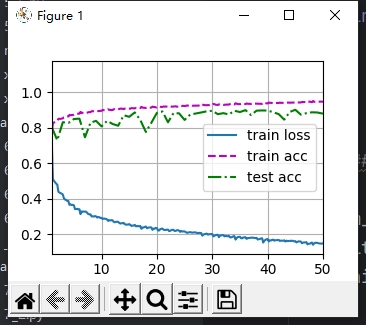
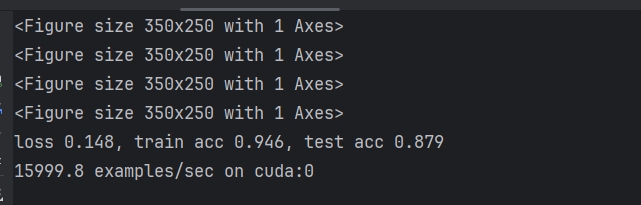
分别是按照我的方法与文章方法的结果。
BatchNorm()类定义中每次调用该类的时候,其中的moving_mean都会被初始化为0;那么这还符合moving_mean的定义吗?因为好像就只使用了一个batch的数据进行计算;
按照指数移动平均的计算
moving_mean = momentum* moving_mean + (1-momentum)mean
中momentum moving_mean的moving_mean不是应该是上一个batch计算得到的结果?
也就是说,咱这个moving_mean应该是定义成一个全局性的变量才对吧
关于第一问,偏置的维度和BN计算平均和方差的维度不一致哦,也就是说计算平均时每个数值中的偏置并不完全相同,所以不能抵消掉