https://zh.d2l.ai/chapter_convolutional-neural-networks/conv-layer.html
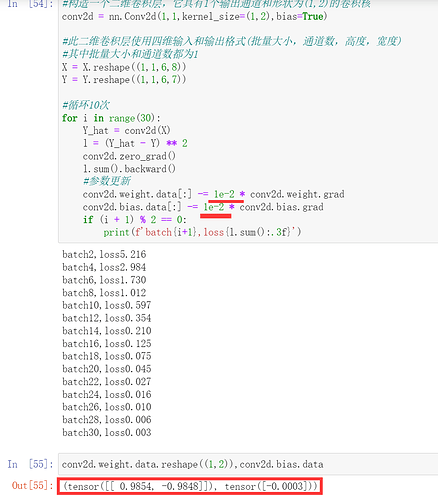
请问在6.2.4中，将bias设置为True，迭代卷积核时加上
conv2d.bias.data -= 0.03 * conv2d.bias.grad，结果无法正常收敛，是什么原因呢
1 Like
应该是学习率太大的问题，把学习率调到0.003，同时增加迭代轮次好像就能收敛了。
2 Likes
上面 corr2d的函数实现应该注明一下是在strid=1情况下得实现吧
练习二问的 Conv2D 自动求导时，有什么错误消息啊，请问有人发现吗
有人遇到这个错吗？
34 from pandas._typing import FrameOrSeries, FrameOrSeriesUnion
—> 35 from pandas.util._decorators import Appender, Substitution, doc
36
37 from pandas.core.dtypes.cast import (
ImportError: cannot import name ‘doc’
好像没有错误消息~
但是只能计算2维张量
1 Like
3，把输入和卷积展平，卷积核每滑动一个步幅取一个样本。
4.1.二阶导数卷积核就是拉普拉斯算子[[0,1,0],[1,-4,1],[0,1,0]]
4.2 d+1
X = torch.eye((8))
print(“⼀个6 × 8像素的单位矩阵图像 : \n”, X)
K = torch.tensor([[1.0, -1.0]])
Y = corr2d(X, K)
print(“互相关运算 : \n”, Y)
print(“corr2d(X.t(), K) : \n”, corr2d(X.t(), K))
print(“corr2d(X.t(), K) : \n”, corr2d(X.t(), K.t()))
结果就是:
tensor([[ 1., 0., 0., 0., 0., 0., 0.],
[-1., 1., 0., 0., 0., 0., 0.],
[ 0., -1., 1., 0., 0., 0., 0.],
[ 0., 0., -1., 1., 0., 0., 0.],
[ 0., 0., 0., -1., 1., 0., 0.],
[ 0., 0., 0., 0., -1., 1., 0.],
[ 0., 0., 0., 0., 0., -1., 1.],
[ 0., 0., 0., 0., 0., 0., -1.]])
如果转置X结果不变。
如果转置K结果也会转置。变成：
tensor([[ 1., -1., 0., 0., 0., 0., 0., 0.],
[ 0., 1., -1., 0., 0., 0., 0., 0.],
[ 0., 0., 1., -1., 0., 0., 0., 0.],
[ 0., 0., 0., 1., -1., 0., 0., 0.],
[ 0., 0., 0., 0., 1., -1., 0., 0.],
[ 0., 0., 0., 0., 0., 1., -1., 0.],
[ 0., 0., 0., 0., 0., 0., 1., -1.]])
2 Likes
Question1:
def diag(X):
for i in range(X.shape[0]):
for j in range(X.shape[1]):
if i == j:
X[i,j] = 0
return X
把矩阵的对角线上元素只为零，然后kernel是1*2的，检测结果是对角线上面是-1下面是1，X转置后结果是一样的，K转置后就是把上面的结果转置。
2 Likes
Q1: 构建一个具有对角线边缘的图像X。
X = torch.eye(4)
print(X)
K = torch.tensor([[1.0, -1.0]])
# 如果将本节中举例的卷积核K应用于X，会发生什么情况？
print(corr2d(X, K))
# 如果转置X会发生什么？
# X转置后，结果不变
print(corr2d(X.t(), K))
# 如果转置K会发生什么？
# K转置后，结果也转置了
print(print(corr2d(X, K.t())))
Q2: 在我们创建的Conv2D自动求导时，有什么错误消息？
A2: 没搞懂啥意思，上面创建的Conv2D不是已经进行自动求导了吗？运行没有error啊…
Q3: 如何通过改变输入张量和卷积核张量，将互相关运算表示为矩阵乘法？
A3: 题目的意思就是如何通过 矩阵乘法 得到 互相关（卷积）运算。
def conv2d_by_mul(X, K):
inh, inw = X.shape
h, w = K.shape
outh = inh - h + 1
outw = inw - w + 1
K = K.reshape(1, -1)
XX = torch.zeros(K.shape[1], outh * outw)
k = 0
for i in range(outh):
for j in range(outw):
XX[:, k] = X[i:i + h, j:j + w].reshape(-1)
k += 1
# 用矩阵乘法表示互相关运算
res = (torch.mm(K, XX)).reshape(outh, outw)
return res
X = torch.randn((4, 4))
K = torch.tensor([[0.0, 1.0], [2.0, 3.0]])
print(corr2d(X, K))
print(conv2d_by_mul(X, K))
Q4: 手工设计一些卷积核…
A4: 可参考https://dsp.stackexchange.com/questions/10605/kernels-to-compute-second-order-derivative-of-digital-image
4 Likes
A3的conv2d_by_mul函数有bug，修改后如下
def conv2d_by_mul(X, K):
h, w = K.shape
outh = X.shape[0] - h + 1
outw = X.shape[1] - w + 1
K = K.reshape(-1, 1)
Y = []
for i in range(outh):
for j in range(outw):
Y.append(X[i:i + h, j:j + w].reshape(-1))
# 这个完全没想到，感谢@thirty
Y = torch.stack(Y, 0)
# 用矩阵乘法表示互相关运算
res = (torch.matmul(Y, K)).reshape(outh, outw)
return res
3 Likes
问题二： 1. 在我们创建的Conv2D自动求导时，有什么错误消息？
错误信息：The size of tensor a (0) must match the size of tensor b (7) at non-singleton dimension 3
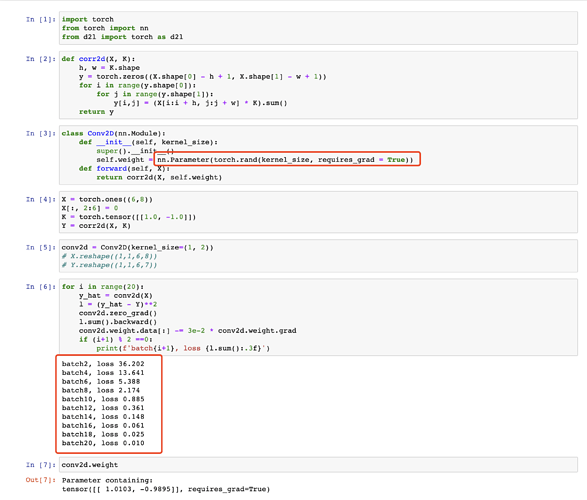
会提示维度不对称的错误信息，因为torch提供的二维卷积层是nn.Conv2d() 采用的是四维输入和输出格式（批量大小、通道、高度、宽度）,而我们自定义的仅仅是二维的，因此代码可以修改为：
conv2d = Conv2D(kernel_size=(1, 2))
X = X.reshape(( 6, 8))
Y = Y.reshape(( 6, 7))
print(X)
print(Y)
lr = 3e-2 # 学习率
for i in range(10):
Y_hat = conv2d(X)
print(Y_hat.shape)
l = (Y_hat - Y) ** 2
conv2d.zero_grad()
l.sum().backward()
conv2d.weight.data[:] -= lr * conv2d.weight.grad
if (i + 1) % 2 == 0:
print(f’epoch {i+1}, loss {l.sum():.3f}’)
3 Likes
conv2d = Conv2D(kernel_size=(1, 2))
X = X.reshape(( 6, 8))
Y = Y.reshape(( 6, 7))
print(X)
print(Y)
lr = 3e-2 # 学习率
for i in range(10):
Y_hat = conv2d(X)
print(Y_hat.shape)
l = (Y_hat - Y) ** 2
conv2d.zero_grad()
l.sum().backward()
conv2d.weight.data[:] -= lr * conv2d.weight.grad
if (i + 1) % 2 == 0:
print(f’epoch {i+1}, loss {l.sum():.3f}’)
改了一下代码格式，看起来更舒服一点，哈哈
0.03的学习率还是挺大的，最好设置更小一些
1 Like
我的理解是初始化权重参数，有助于反向传播时更新梯度，加速收敛