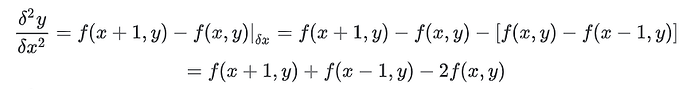图像卷积

中文版 pytorch
23

第三题，矩阵转置运算后取主对角线之和即可

1
12085×684 85.6 KB

24

本身就是借助torch的框架，计算梯度没啥问题，但是自己定义的网络，只能计算2维矩阵

25

  1. 构建一个具有对角线边缘的图像X

    X = torch.eye(8)
X

    tensor([[1., 0., 0., 0., 0., 0., 0., 0.],
        [0., 1., 0., 0., 0., 0., 0., 0.],
        [0., 0., 1., 0., 0., 0., 0., 0.],
        [0., 0., 0., 1., 0., 0., 0., 0.],
        [0., 0., 0., 0., 1., 0., 0., 0.],
        [0., 0., 0., 0., 0., 1., 0., 0.],
        [0., 0., 0., 0., 0., 0., 1., 0.],
        [0., 0., 0., 0., 0., 0., 0., 1.]])

    1. 如果将本节中举例的卷积核K应用于X，会发生什么情况？

      Y = corr2d(X,K)
Y

      tensor([[ 1.,  0.,  0.,  0.,  0.,  0.,  0.],
        [-1.,  1.,  0.,  0.,  0.,  0.,  0.],
        [ 0., -1.,  1.,  0.,  0.,  0.,  0.],
        [ 0.,  0., -1.,  1.,  0.,  0.,  0.],
        [ 0.,  0.,  0., -1.,  1.,  0.,  0.],
        [ 0.,  0.,  0.,  0., -1.,  1.,  0.],
        [ 0.,  0.,  0.,  0.,  0., -1.,  1.],
        [ 0.,  0.,  0.,  0.,  0.,  0., -1.]])

    2. 如果转置X会发生什么？

      Y = corr2d(X.t(),K)
Y

      tensor([[ 1.,  0.,  0.,  0.,  0.,  0.,  0.],
        [-1.,  1.,  0.,  0.,  0.,  0.,  0.],
        [ 0., -1.,  1.,  0.,  0.,  0.,  0.],
        [ 0.,  0., -1.,  1.,  0.,  0.,  0.],
        [ 0.,  0.,  0., -1.,  1.,  0.,  0.],
        [ 0.,  0.,  0.,  0., -1.,  1.,  0.],
        [ 0.,  0.,  0.,  0.,  0., -1.,  1.],
        [ 0.,  0.,  0.,  0.,  0.,  0., -1.]])

    3. 如果转置K会发生什么？

      Y = corr2d(X,K.t())
Y

      tensor([[ 1., -1.,  0.,  0.,  0.,  0.,  0.,  0.],
        [ 0.,  1., -1.,  0.,  0.,  0.,  0.,  0.],
        [ 0.,  0.,  1., -1.,  0.,  0.,  0.,  0.],
        [ 0.,  0.,  0.,  1., -1.,  0.,  0.,  0.],
        [ 0.,  0.,  0.,  0.,  1., -1.,  0.,  0.],
        [ 0.,  0.,  0.,  0.,  0.,  1., -1.,  0.],
        [ 0.,  0.,  0.,  0.,  0.,  0.,  1., -1.]])

  2. 在我们创建的Conv2D自动求导时，有什么错误消息？

    没什么错误信息
    本身就是借助torch的框架，计算梯度没啥问题，但是自己定义的网络，只能计算2维矩阵

  3. 如何通过改变输入张量和卷积核张量，将互相关运算表示为矩阵乘法？

    def conv2d_by_mul(X, K):
    h, w = K.shape
    outh = X.shape[0] - h + 1
    outw = X.shape[1] - w + 1
    K = K.reshape(-1, 1)
    Y = []   # 张量列表
    for i in range(outh):
        for j in range(outw):
            Y.append(X[i:i + h, j:j + w].reshape(-1))  # 列表的每一个元素是对应位置卷积核大														 # 小的X内元素 摊开成一维张量

    print(Y)
    Y = torch.stack(Y, 0)                              #升维
    print(Y.shape,K.shape)
    # 用矩阵乘法表示互相关运算
    res = (torch.matmul(Y, K)).reshape(outh, outw)     #矩阵乘法运算后 reshape 成输出大小
    return res

    Y = conv2d_by_mul(X,K)
Y

    [tensor([1., 0.]), tensor([0., 0.]), tensor([0., 0.]), tensor([0., 0.]), tensor([0., 0.]), tensor([0., 0.]), tensor([0., 0.]), tensor([0., 1.]), tensor([1., 0.]), tensor([0., 0.]), tensor([0., 0.]), tensor([0., 0.]), tensor([0., 0.]), tensor([0., 0.]), tensor([0., 0.]), tensor([0., 1.]), tensor([1., 0.]), tensor([0., 0.]), tensor([0., 0.]), tensor([0., 0.]), tensor([0., 0.]), tensor([0., 0.]), tensor([0., 0.]), tensor([0., 1.]), tensor([1., 0.]), tensor([0., 0.]), tensor([0., 0.]), tensor([0., 0.]), tensor([0., 0.]), tensor([0., 0.]), tensor([0., 0.]), tensor([0., 1.]), tensor([1., 0.]), tensor([0., 0.]), tensor([0., 0.]), tensor([0., 0.]), tensor([0., 0.]), tensor([0., 0.]), tensor([0., 0.]), tensor([0., 1.]), tensor([1., 0.]), tensor([0., 0.]), tensor([0., 0.]), tensor([0., 0.]), tensor([0., 0.]), tensor([0., 0.]), tensor([0., 0.]), tensor([0., 1.]), tensor([1., 0.]), tensor([0., 0.]), tensor([0., 0.]), tensor([0., 0.]), tensor([0., 0.]), tensor([0., 0.]), tensor([0., 0.]), tensor([0., 1.])]

torch.Size([56, 2]) torch.Size([2, 1])

    Out[72]:

    tensor([[ 1.,  0.,  0.,  0.,  0.,  0.,  0.],
        [-1.,  1.,  0.,  0.,  0.,  0.,  0.],
        [ 0., -1.,  1.,  0.,  0.,  0.,  0.],
        [ 0.,  0., -1.,  1.,  0.,  0.,  0.],
        [ 0.,  0.,  0., -1.,  1.,  0.,  0.],
        [ 0.,  0.,  0.,  0., -1.,  1.,  0.],
        [ 0.,  0.,  0.,  0.,  0., -1.,  1.],
        [ 0.,  0.,  0.,  0.,  0.,  0., -1.]])

stack: 参考

沿着一个新维度对输入张量序列进行连接。 序列中所有的张量都应该为相同形状。

浅显说法：把多个2维的张量凑成一个3维的张量；多个3维的凑成一个4维的张量…以此类推，也就是在增加新的维度进行堆叠。扩张再拼接

和 cat的 区别： cat不会升维，stack 会先升维再拼接

T1 = torch.tensor([[1, 2, 3],
                 [4, 5, 6],
                 [7, 8, 9]])
 # 假设是时间步T2
T2 = torch.tensor([[10, 20, 30],
                 [40, 50, 60],
                 [70, 80, 90]])
print(torch.stack((T1,T2),dim=0))
print(torch.cat((T1,T2),dim=0))

tensor([[[ 1,  2,  3],
         [ 4,  5,  6],
         [ 7,  8,  9]],

        [[10, 20, 30],
         [40, 50, 60],
         [70, 80, 90]]])
tensor([[ 1,  2,  3],
        [ 4,  5,  6],
        [ 7,  8,  9],
        [10, 20, 30],
        [40, 50, 60],
        [70, 80, 90]])

参数

  • inputs : 待连接的张量序列。 注：python的序列数据只有list和tuple。
  • dim : 新的维度， 必须在0到len(outputs)之间。 注：len(outputs)是生成数据的维度大小，也就是outputs的维度值。
26

请问一下，有人知道第四题怎么做吗？… :saluting_face:

27

[[1,-2, 1]]，这是x方向的2阶导数核函数，

image
image867×114 15.3 KB

28

个人觉得问题中的“导数”的概念不太好理解，以及notebook的例子中使用的[1,-1]这个kernel为什么就能区分左右边界。搜到了这样一个note，感觉对于理解这一节有些帮助https://inst.eecs.berkeley.edu/~cs194-26/fa17/Lectures/ConvEdgesTemplate.pdf

29 
"""Q3"""
def corr2d_matmul(X, K): 
    """计算二维互相关运算"""
    (Xh, Xw), (Kh, Kw) = X.shape, K.shape
    Yh, Yw = Xh - Kh + 1, Xw - Kw + 1
    Y = torch.zeros((Yh, Yw, Kh * Kw))
    for i in range(Yh):
        for j in range(Yw):
            Y[i, j] = X[i:i + Kh, j:j + Kw].reshape(-1)
    return Y @ K.reshape(-1)

X = torch.tensor([[0.0, 1.0, 2.0], [3.0, 4.0, 5.0], [6.0, 7.0, 8.0]])
K = torch.tensor([[0.0, 1.0], [2.0, 3.0]])
corr2d_matmul(X, K)