与模型的超参数设置相关，想要在较短的epoch获得较好的效果，可以初始化参数为目标解，并降低学习率，可以尝试
设置的代码如下：
def train(net,train_features, test_features, train_labels, test_labels,
num_epochs=200):
loss = nn.MSELoss(reduction='mean')
# 不设置偏置，因为我们已经在多项式中实现了它
batch_size = min(10, train_labels.shape[0])
train_iter = d2l.load_array((train_features, train_labels.reshape(-1,1)),
batch_size)
test_iter = d2l.load_array((test_features, test_labels.reshape(-1,1)),
batch_size, is_train=False)
trainer = torch.optim.SGD(net.parameters(), lr=0.003)
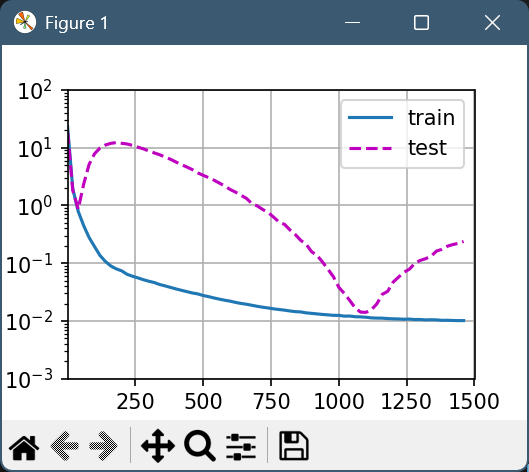
# animator = d2l.Animator(xlabel='epoch', ylabel='loss', yscale='log',
# xlim=[1, num_epochs], ylim=[1e-3, 1e2],
# legend=['train', 'test'])
for epoch in range(num_epochs):
d2l.train_epoch_ch3(net, train_iter, loss, trainer)
# if epoch == 0 or (epoch + 1) % 20 == 0:
# animator.add(epoch + 1, (evaluate_loss(net, train_iter, loss),
# evaluate_loss(net, test_iter, loss)))
return evaluate_loss(net, test_iter, loss)
test_loss=[]
# 从多项式特征中选择前4个维度，即1,x,x^2/2!,x^3/3!'
import matplotlib.pyplot as plt
for i in range(3,20):
train_features = poly_features[:n_train, :i]
test_features = poly_features[n_train:, :i]
input_shape = train_features.shape[-1]
net = nn.Sequential(
nn.Linear(input_shape, 1, bias=False),
# nn.ReLU()
)
test_loss.append(train(net,train_features,test_features,labels[:n_train], labels[n_train:]))
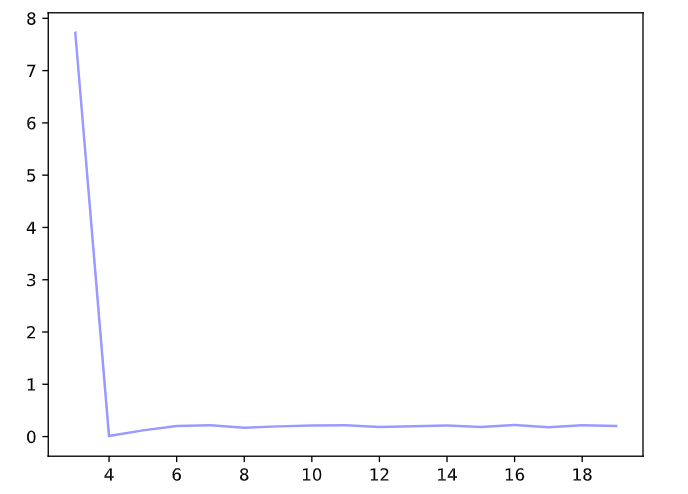
plt.plot(np.arange(3,20), test_loss, label='test loss',color='blue',alpha=0.4)
plt.show()
1 Like
修改 N_TRAIN 至 50 得到，实际上当 N_TRAIN 很大时，这一测试也能得到很好的拟合（高于四阶的系数拟合至 0）
2.考虑多项式的模型选择。
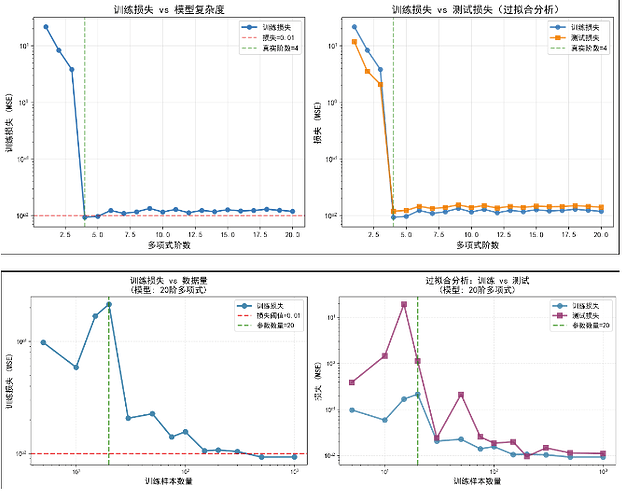
1. 绘制训练损失与模型复杂度（多项式的阶数）的关系图。观察到了什么？需要多少阶的多项式才能将训练损失减少到0?
2. 在这种情况下绘制测试的损失图。
3. 生成同样的图，作为数据量的函数。
数据生成：真实模型为 4 阶多项式
训练样本：100，测试样本：100
每个模型训练 800 轮
训练 1 阶多项式… 训练损失: 21.613440, 测试损失: 11.775331
训练 2 阶多项式… 训练损失: 8.342850, 测试损失: 3.540991
训练 3 阶多项式… 训练损失: 3.821037, 测试损失: 2.083570
训练 4 阶多项式… 训练损失: 0.009329, 测试损失: 0.011918
训练 5 阶多项式… 训练损失: 0.009663, 测试损失: 0.012311
训练 6 阶多项式… 训练损失: 0.012308, 测试损失: 0.014566
训练 7 阶多项式… 训练损失: 0.010888, 测试损失: 0.013332
训练 8 阶多项式… 训练损失: 0.011665, 测试损失: 0.013981
训练 9 阶多项式… 训练损失: 0.013373, 测试损失: 0.015471
训练 10 阶多项式… 训练损失: 0.011589, 测试损失: 0.013915
训练 11 阶多项式… 训练损失: 0.012857, 测试损失: 0.015033
训练 12 阶多项式… 训练损失: 0.011201, 测试损失: 0.013577
训练 13 阶多项式… 训练损失: 0.012351, 测试损失: 0.014569
训练 14 阶多项式… 训练损失: 0.011734, 测试损失: 0.013977
训练 15 阶多项式… 训练损失: 0.012675, 测试损失: 0.014701
训练 16 阶多项式… 训练损失: 0.012060, 测试损失: 0.014376
训练 17 阶多项式… 训练损失: 0.012319, 测试损失: 0.014444
训练 18 阶多项式… 训练损失: 0.012916, 测试损失: 0.014948
训练 19 阶多项式… 训练损失: 0.012402, 测试损失: 0.014585
训练 20 阶多项式… 训练损失: 0.011871, 测试损失: 0.014093
模型复杂度：20 阶多项式 (20 个参数)
真实模型：4 阶多项式
测试集大小：固定100个样本
训练轮数：800
训练集大小: 5 | 训练损失: 0.098009 | 测试损失: 0.388081
训练集大小: 10 | 训练损失: 0.058765 | 测试损失: 1.460117
训练集大小: 15 | 训练损失: 0.168437 | 测试损失: 19.184912
训练集大小: 20 | 训练损失: 0.214649 | 测试损失: 1.134060
训练集大小: 30 | 训练损失: 0.020649 | 测试损失: 0.024168
训练集大小: 50 | 训练损失: 0.022645 | 测试损失: 0.213310
训练集大小: 75 | 训练损失: 0.014048 | 测试损失: 0.025548
训练集大小: 100 | 训练损失: 0.015633 | 测试损失: 0.018688
训练集大小: 150 | 训练损失: 0.010580 | 测试损失: 0.019887
训练集大小: 200 | 训练损失: 0.010740 | 测试损失: 0.009552
训练集大小: 300 | 训练损失: 0.010425 | 测试损失: 0.014692
训练集大小: 500 | 训练损失: 0.009295 | 测试损失: 0.011417
训练集大小: 1000 | 训练损失: 0.009312 | 测试损失: 0.011152
-
数据生成过程完全确定（无随机噪声）
y = f(x)，不存在ε -
模型能完美表达真实函数
存在参数 θ* 使得 f_θ*(x) = f(x) 对所有 x ∈ 𝒳 -
训练算法能找到这个完美参数
优化算法收敛到全局最优 θ* -
测试数据分布与训练数据一致
P_test(x) = P_train(x)
在吴恩达的课上，他把线性回归和多项式回归放在一起讲了，因为他们都是线性模型。
所谓多项式回归本质就是收集特征的时候（比如收集到了房子的长和宽），敏锐的意识到问题其实和特征的组合关联性很强（房子的长、宽当然一定程度上决定房价，但是毋庸置疑的是长宽这两个特征组合的面积更关键，因为长条型的房子在实际问题中几乎不存在可以忽略不计，相比于只看长宽、面积主导房价）
回到这里，这个多项式中线性的部分只有红框圈起来的这些，如果你要去学x的指数、分子的阶乘规律，这些东西变为w的话，会导致非线性，没法梯度下降（此时的优化指导原理还是因为问题线性所以、用梯度下降最小化代价得到的局部最优解是全局最优解呢）。
同时从代码实现的角度看，x和自己的复合（下标导致的阶乘、系数），提前算（把feature早早的就算成polyfeature）和 作为红框圈起来的w的梯度用到的时候再算没区别。
所以无论只是x和自己的复合，还是x1x2x3…xn的反对幂三指复合，只要他们还是线性模型（求导是偏w），都是提前算出来方便一点。
所以多项式回归局限性其实很大很大，他要求你必须明确知道这个函数长什么样子，然后去猜系数。所以吴恩达把他们放在第一讲就讲了，只作为入门内容。