我想应该不是的，应当是：
P(A, B, C) = P(C | A, B) P(A, B) = P(C | A, B) P(B | A) P(A)
1 Like
您好，直觉上来说，如果第一种测试进行两次的结果是独立的，那么就是不光测试是独立的，人也是独立的（两个不同的人）。所以两个不同的人分别进行测试显示阳性而实际患病的概率自然更低。
个人理解希望对你有所帮助。
1 Like
如果这个可以证明P(A,B,C)=P(A)P(B|A)P(C|B)
那么就有下面这样的逻辑了
P(A,B,C)=P(A)P(B|A)P(C|B)
=P(A) * (P(A|B)*P(B)/P(A)) * (P(B|C)*P(C)/P(B))
=P(A) * (P(A)*P(B)/P(A)) * (P(B)*P(C)/P(B))
=P(A) * P(B) * P(C)
是这样吗？看起来挺简洁的，有没有数学好的，解释一下答案对不对
第三题：
后面的概率都是基于前面已经事件发生的基础上给出的，即条件概率。所以计算概率P(A·B·C)的概率分布时，应该有：
P(A·B·C) = P(A) * P(B|A)*P(C|B)
A和B不是独立的，P(A|B) ≠ P(A)
Q1:进行m = 500组实验,每组抽取n = 10个样本。改变m和n,观察和分析实验结果。
# 2.6.1 进行m = 500组实验,每组抽取n = 10个样本。改变m和n,观察和分析实验结果。
counts_l = multinomial.Multinomial(10, fair_probs).sample((500,))
counts_h = multinomial.Multinomial(100, fair_probs).sample((600,))
cum_counts_l = counts_l.cumsum(dim=0)
cum_counts_h = counts_h.cumsum(dim=0)
estimates_l = cum_counts_l / cum_counts_l.sum(dim=1, keepdims=True)
estimates_h = cum_counts_h / cum_counts_h.sum(dim=1, keepdims=True)
d2l.set_figsize((6, 4.5))
for i in range(6):
d2l.plt.plot(estimates_l[:, i].numpy(),
label=("P(die=" + str(i + 1) + ")"))
d2l.plt.axhline(y=0.167, color='black', linestyle='dashed')
d2l.plt.gca().set_xlabel('10 Groups of experiments')
d2l.plt.gca().set_ylabel('Group1 Estimated probability')
# d2l.plt.gca()
d2l.plt.legend();
d2l.plt.show()
d2l.set_figsize((6, 4.5))
for i in range(6):
d2l.plt.plot(estimates_h[:, i].numpy(),
label=("P(die=" + str(i + 1) + ")"))
d2l.plt.axhline(y=0.167, color='black', linestyle='dashed')
d2l.plt.gca().set_xlabel('100 Groups of experiments')
d2l.plt.gca().set_ylabel('Group2 Estimated probability')
# d2l.plt.gca()
d2l.plt.legend();
Q2:给定两个概率为P (A)和P (B)的事件,计算P (A ∪ B)和P (A ∩ B)的上限和下限。(提示:使用友元图43来 展示这些情况。)
A2:感觉是1和0
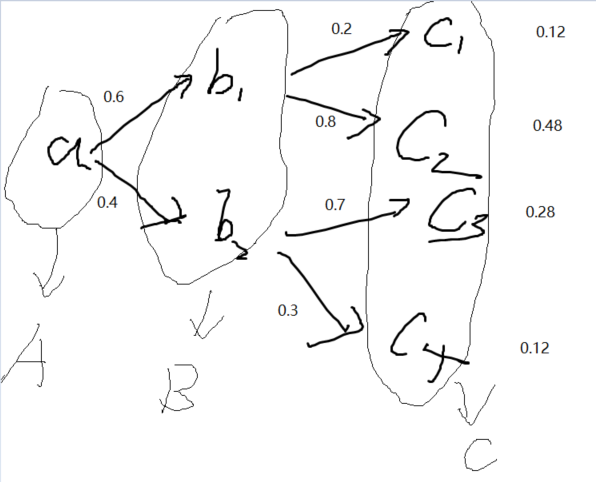
Q3:假设我们有一系列随机变量,例如A、B和C,其中B只依赖于A,而C只依赖于B,能简化联合概 率P (A, B, C)吗?
A3:
Q4:在 2.6.2节中,第一个测试更准确。为什么不运行第一个测试两次,而是同时运行第一个和第二个测试?
A4:引用
1 Like
如果假设两次使用第一个测试独立：
是不是有P(D1=1,D’1=1)=P(D1=1)xP(D’1=1)
但这样算的结果不对（大于1）。
import torch
from torch.distributions import multinomial as mulno
from d2l import torch as d2l
def throw(m, n):
probs = torch.ones(6)/6
# m, n = 500, 10
expr = mulno.Multinomial(n, probs).sample([m,])
cnts = expr.cumsum(dim=0)
estm = cnts / cnts.sum(dim=1, keepdims=True)
for i in range(6):
d2l.plt.plot(list(range(1,m+1)), estm[:, i], label=f"(die={i+1})")
# d2l.plt.plot(estm.T.numpy(), label=[f"(die={i+1})" for i in range(6)])
d2l.plt.axhline(y=0.167, color='black', linestyle='dashed')
d2l.plt.gca().set_xlabel('Groups of experiments')
d2l.plt.gca().set_ylabel('Estimated probability')
d2l.plt.gca().set_ylim(0, 0.5)
d2l.plt.legend()
d2l.plt.title(f"{n} throws, {m} times")
d2l.plt.show()
throw(500, 10)
throw(50, 100)
throw(5, 1000)
throw(5000, 1)
1 Like
应该就是真实值，概率的关键在于集合不同元素进行映射的权重，所以这里指的是真实值
2.6.1
增加 m，我们就增加了第一次采样的样本量，带来的结果是取样图上下限降低。反之亦然。极端情况是取 m=1，此时第一次取样有一个点概率为1而其他所有点概率均为0
增加 n，绘图有更多样本点。但是当数据量收敛至一定量后概率波动量就大大降低（使用切比雪夫不等式）
2.6.2
$$
\max{P(A), P(B)} \leq P(A \cup B) \geq P(A) + P(B)
$$
事实上，$P(A\cup B) = P(A) + P(B) - P(AB)$。
2.6.3
$$
P(ABC) = P(C|AB)P(AB) = P(C|B)P(AB) = P(C|B)P(B|A)P(A)
$$
2.6.4
因果图解释
检验样品的因果图如下，得了H 和 混淆因素（比方说你先天白细胞浓度多于常人，让检测试剂误判）共同影响检测结果。
得了H → 检测阳性 ← 混淆因素（如身体原因）
检测出现失误为检验靶点无法排除的混淆因素影响，你重新测第一个测试还是没办法排除全部混淆因素，因此没办法（在因果关系下）增加信心。
概率论解释
两次运行第一个测试，两次测试的相关性较大且无法排除。比方说，两次测试有50%可能性使得第二次测试完全等同于第一次测试结果，那么两次测试后的取信度为：
$$
\begin{align}
P(H=1|D_1 = 1,D_2 = 1) &= \dfrac{P(D_1 = 1, D_2 = 1|H = 1)P(H)}{P(D_1 = 1,D_2 = 1)}\
P(D_1 = 1, D_2 = 1|H = 1) &= 1\\
P(D_1 = 1, D_2 = 1) &= P(D_1 = 1, D_2 = 1|H = 1)P(H=1) + P(D_1 = 1, D_2 = 1|H = 0)P(H=0)\\
P(D_1 = 1, D_2 = 1|H = 0) &= 0.5 \times P(D_1 = 1|H=0) + 0.5 \times P(D_1 = 1|H=0)P(D_2 = 1|H=0)
\end{align}
$$
计算得
$$
\begin{align}
P(D_1 = 1, D_2 = 1|H = 0) &= 0.00505\
P(D_1 = 1, D_2 = 1) &= 0.00664\
P(H=1|D_1 = 1,D_2 = 1) &= 0.0015 / 0.00664 \approx 22.58%
\end{align}
$$
可以看到，即使只有50%相关性，概率也只提升到了22.58%，提升了9%不到。远不如测试一个“不那么好”但是没有混淆因子/几乎不相关的第二个试剂
使用markdown语法，把它复制到拿个markdown编辑器里就能看到数学公式
13.6%是条件概率，第一个13.6%是第一次测试阳性的条件下的患病概率，第二个13.6%是第二次测试阳性的条件下的患病概率，就算题目说满足条件独立性，两个条件不一样，乘起来也没有任何意义
C只依赖B，所以从定义来说，P(C|A,B)=P(C|B)，虽然我还是不知道B依赖A，C是怎么做到依赖B不依赖A的
我也觉得是这个原因，用同一种测试方法进行的两次测试不是两个独立事件。