概率

中文版 pytorch
11

我觉得应该是的，P(A,B,C) = P(A)P(B|A)P(C|B)

1 Like
12

有朋友们分享一下第四题的见解吗 :thinking: :thinking: :thinking:

13

第四题，我觉得是因为使用同一种测试的话，如果没有随机因素的干扰或者测试流程的问题，结果应该是不会变的，所以大概率结果相同，第二次测试就没什么意义。使用不同的测试，可以避免这个问题。个人感觉，仅供参考

3 Likes
14

d2l.plt.plot和d2l.plot有什么区别呢？

15

d2l.plt.plot用的是matplotlib.pyplot.plot()函数，dl2.plot是自己定义的绘图函数

2 Likes
16

第四题中因为第一个测试和第二个测试具有不同的特性，所以可以假定它们条件独立来计算患者真实患病的概率。而测试一和它本身显然是条件不独立的（不能使用bayes定理计算必要概率），而且具有很强的相关关系，因此连续做两次测试一不能更好地判断病人是否患病

5 Likes
17

第一题中的两个参数：
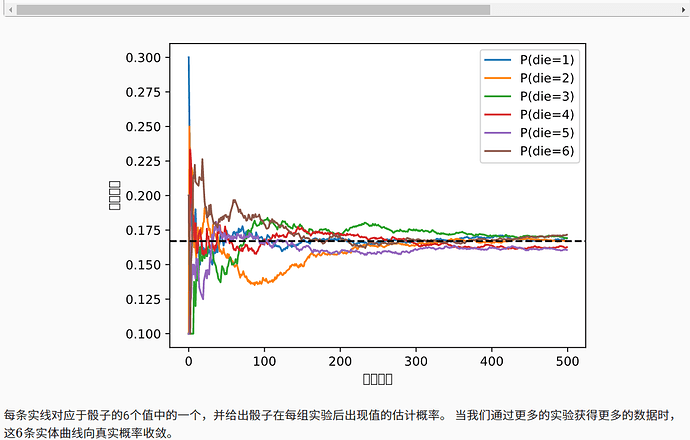
“m=500组实验，每组抽取n=10个样本”
能否这样理解：n个样本对应深度训练框架中的batch_size, m组实验对应batch的个数?
batch_size 越大模型越容易收敛，因为学得是大batch数据的均值；反之越小，越不稳定，极端情况是1的时候，模型不可能收敛了；

第四题，第一个测试两次都是阳性，此时是真阳性的概率是：0.999993
推导过程：

IMG_1801
IMG_18011028×1824 408 KB

1 Like
19

image

20

一个是调用d2l包中自己封装的方法，一个是调用d2l包中matplotlib.pyplot包中方法

1 Like
21

image
image1157×739 59.3 KB

这张图的横纵坐标轴的中文显示乱码
d2l.plt.gca().set_xlabel(‘Groups of experiments’)
d2l.plt.gca().set_ylabel(‘Estimated probability’)

22

有个问题一直困扰我，方便解答一下吗，第一种测试显示阳性实际患病概率是13.6%，不患病的概率就是86.4%；如果再来一次第一种测试，并且是条件独立的，那两次不患病的概率是86.4%*86.4%=0.7465，那患病的概率应该是25%左右啊

1 Like
23

P(A | B’) =1− P(A | B)
P(A,B |C) = P(A,B,C)
P©
P(A | B,C) = P(A,B | B,C)d)
P(A,B,C) = P(A | B,C)P(B |C)P©
我不知道你们咋算的，反正我没看懂第三题，根据马尔科夫决策P(Xt+1|Xt)=P(Xt+1|x0,…xt)，应该是把P(A | B,C)看做P(A|B)吧

1 Like
26

第三题 感觉跟条件概率链式法则有关 A -> B ->C
P(A,B,C) = P(C|A,B)P(A,B) 由于C和A无关P(A,B,C) = P(C|A,B)P(A,B) = P(C|B)P(B|A)
\[quote=“LLCoolJ, post:26, topic:1762, full:true”]
第四题 两种测试有不同特性 不重复使用 可以避免某一种的漏洞

2 Likes
27

Q3:
P(A,B,C) = P(B|A,C)P(A,C),由于C和A无关,说明相互独立
P(A,B,C) = P(B|A,C)P(A)P©
right?

28

应该是两次D1毕竟是使用的同一台机器，没法做到不独立

1 Like
29

WechatIMG655
WechatIMG6551280×1706 83.9 KB

1 Like
30

我觉得无论重复第一种测试多少遍，都无法提供新的有效信息，求出概率不变。

1 Like
31

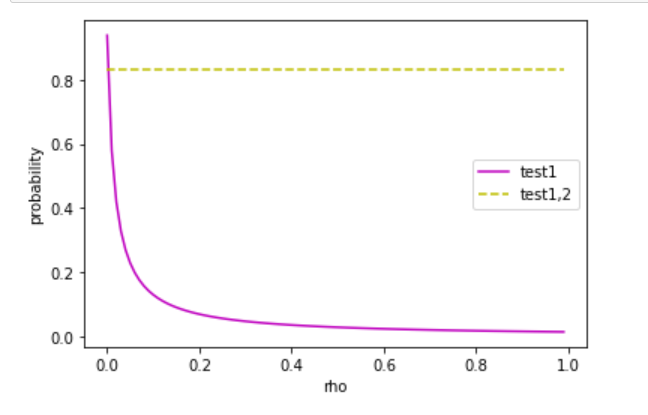
我假设了在H已知条件下两次测试1D_1^1和D_1^2的相关系数为rho,得到了概率
概率图片

1 Like
33

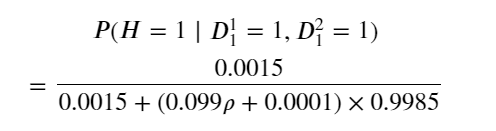
以及概率随rho变化的趋势图，可以看到只要两次测试1有一点相关性，这个概率就会迅速下降
趋势图

4 Likes
34

说一下我对第4题的理解：

前提条件说明一下，帮助大家理解：检测结果为阳性只能说明指标为阳性但是并不是说病人就为阳性。并不能完全说明只要是该指标异常，病人就一定是患病状态，可能是比如病人因为其他原因导致的（也就是P(D = 1, H = 0) ≠ 0）所以才有了检测为阳性不一定患病这个问题。那么如果检测方法1第一次给病人检测为阳性，那么第二次还为阳性的可能性会比较大。也就是说先后两次用同一检测方法检测结果大概率是相关的。

在计算D1和D2的联合概率 P(D1 = 1, D2 = 1 | H = 1) 或者 P(D1 = 1, D2 = 1 | H = 0) 的时候，这里需要注意的是：

  • 如果两个事件独立：
    那么
P(D1 = 1, D2 = 1 | H = 1)  = P(D1 = 1 | H = 1) * P(D2 = 1 | H = 1)
  • 如果两个事件不独立：
P(D1 = 1, D2 = 1 | H = 1)  ≠ P(D1 = 1 | H = 1) * P(D2 = 1 | H = 1)

举个例子，比如小明、小黑是一个班的同学（小黑给小明说好了，考试给他抄一抄），小红是另外一个班的学生。

  • 小明考80分以上的概率是P(小明 > 80) = 0.8；
  • 小黑考80分以上的概率是P(小黑 > 80) = 0.1；
  • 小红考80分以上的概率是P(小红 > 80) = 0.1。

在一次考试中，请问，小明、小黑同时考80分以上的概率和小明、小红都考80分以上的概率相同吗？

很显然不同，前面的概率会小于0.8，但是会大于0.8 * 0.1 = 0.08，当然小黑可能抄不全；后者的概率为0.8 * 0.1 = 0.08。

可以想象，因为两个测试不独立，导致分母P(D1 = 1, D2 = 1)可能会极其的大（因为相互关联，P(D1 = 1)的同时几乎P(D1 = 1)），最后计算出来的病人阳性的概率也不高。

想请教一下，就是如果事件不独立，那么联合概率的计算应该是怎样的。

8 Likes