文中标准差的英文写错了![]()
第三问的马尔可夫链怎么做呀,有人会说一下呗
第三题简化到 P(AB)P(BC) 不知道对不对
请问第四题何解?按照两次独立D1计算明明结果更好
请问一下第三题怎么做呀?有没有大佬会的写一下过程
是不是 P(A,B,C) = P(A)P(B|A)P(C|B)
作图的那个代码我运行不了哦
一运行,内核就掉了
“形式上, 概率 (probability)可以被认为是将集合映射到真实值的函数。”
此处“真实值”应为“实数”吧
我觉得应该是的,P(A,B,C) = P(A)P(B|A)P(C|B)
有朋友们分享一下第四题的见解吗 


第四题,我觉得是因为使用同一种测试的话,如果没有随机因素的干扰或者测试流程的问题,结果应该是不会变的,所以大概率结果相同,第二次测试就没什么意义。使用不同的测试,可以避免这个问题。个人感觉,仅供参考
d2l.plt.plot和d2l.plot有什么区别呢?
d2l.plt.plot用的是matplotlib.pyplot.plot()函数,dl2.plot是自己定义的绘图函数
第四题中因为第一个测试和第二个测试具有不同的特性,所以可以假定它们条件独立来计算患者真实患病的概率。而测试一和它本身显然是条件不独立的(不能使用bayes定理计算必要概率),而且具有很强的相关关系,因此连续做两次测试一不能更好地判断病人是否患病
第一题中的两个参数:
“m=500组实验,每组抽取n=10个样本”
能否这样理解:n个样本对应深度训练框架中的batch_size, m组实验对应batch的个数?
batch_size 越大模型越容易收敛,因为学得是大batch数据的均值;反之越小,越不稳定,极端情况是1的时候,模型不可能收敛了;
第四题,第一个测试两次都是阳性,此时是真阳性的概率是:0.999993
推导过程:
![]()
一个是调用d2l包中自己封装的方法,一个是调用d2l包中matplotlib.pyplot包中方法
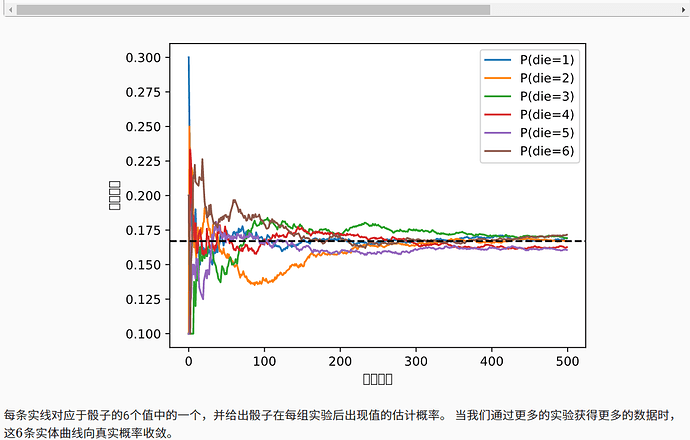
这张图的横纵坐标轴的中文显示乱码
d2l.plt.gca().set_xlabel(‘Groups of experiments’)
d2l.plt.gca().set_ylabel(‘Estimated probability’)
有个问题一直困扰我,方便解答一下吗,第一种测试显示阳性实际患病概率是13.6%,不患病的概率就是86.4%;如果再来一次第一种测试,并且是条件独立的,那两次不患病的概率是86.4%*86.4%=0.7465,那患病的概率应该是25%左右啊