P(A | B’) =1− P(A | B)
P(A,B |C) = P(A,B,C)
P©
P(A | B,C) = P(A,B | B,C)d)
P(A,B,C) = P(A | B,C)P(B |C)P©
我不知道你们咋算的，反正我没看懂第三题，根据马尔科夫决策P(Xt+1|Xt)=P(Xt+1|x0,…xt)，应该是把P(A | B,C)看做P(A|B)吧
1 Like
第三题 感觉跟条件概率链式法则有关 A -> B ->C
P(A,B,C) = P(C|A,B)P(A,B) 由于C和A无关P(A,B,C) = P(C|A,B)P(A,B) = P(C|B)P(B|A)
\[quote=“LLCoolJ, post:26, topic:1762, full:true”]
第四题 两种测试有不同特性 不重复使用 可以避免某一种的漏洞
2 Likes
Q3:
P(A,B,C) = P(B|A,C)P(A,C),由于C和A无关,说明相互独立
P(A,B,C) = P(B|A,C)P(A)P©
right?
应该是两次D1毕竟是使用的同一台机器，没法做到不独立
1 Like
我觉得无论重复第一种测试多少遍，都无法提供新的有效信息，求出概率不变。
1 Like
我假设了在H已知条件下两次测试1D_1^1和D_1^2的相关系数为rho,得到了概率
1 Like
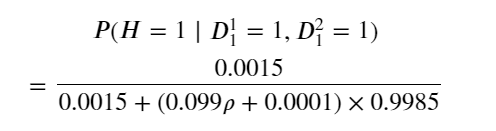
以及概率随rho变化的趋势图，可以看到只要两次测试1有一点相关性，这个概率就会迅速下降
4 Likes
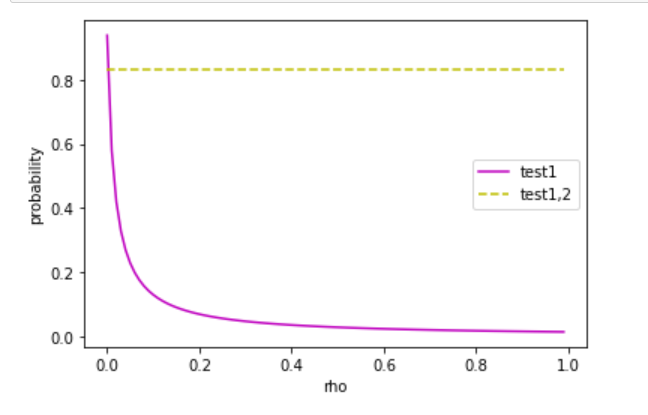
说一下我对第4题的理解：
前提条件说明一下，帮助大家理解：检测结果为阳性只能说明指标为阳性但是并不是说病人就为阳性。并不能完全说明只要是该指标异常，病人就一定是患病状态，可能是比如病人因为其他原因导致的（也就是P(D = 1, H = 0) ≠ 0）所以才有了检测为阳性不一定患病这个问题。那么如果检测方法1第一次给病人检测为阳性，那么第二次还为阳性的可能性会比较大。也就是说先后两次用同一检测方法检测结果大概率是相关的。
在计算D1和D2的联合概率 P(D1 = 1, D2 = 1 | H = 1) 或者 P(D1 = 1, D2 = 1 | H = 0) 的时候，这里需要注意的是：
- 如果两个事件独立：
那么
P(D1 = 1, D2 = 1 | H = 1) = P(D1 = 1 | H = 1) * P(D2 = 1 | H = 1)
- 如果两个事件不独立：
P(D1 = 1, D2 = 1 | H = 1) ≠ P(D1 = 1 | H = 1) * P(D2 = 1 | H = 1)
举个例子，比如小明、小黑是一个班的同学（小黑给小明说好了，考试给他抄一抄），小红是另外一个班的学生。
- 小明考80分以上的概率是
P(小明 > 80) = 0.8； - 小黑考80分以上的概率是
P(小黑 > 80) = 0.1； - 小红考80分以上的概率是
P(小红 > 80) = 0.1。
在一次考试中，请问，小明、小黑同时考80分以上的概率和小明、小红都考80分以上的概率相同吗？
很显然不同，前面的概率会小于0.8，但是会大于0.8 * 0.1 = 0.08，当然小黑可能抄不全；后者的概率为0.8 * 0.1 = 0.08。
可以想象，因为两个测试不独立，导致分母P(D1 = 1, D2 = 1)可能会极其的大（因为相互关联，P(D1 = 1)的同时几乎P(D1 = 1)），最后计算出来的病人阳性的概率也不高。
想请教一下，就是如果事件不独立，那么联合概率的计算应该是怎样的。
7 Likes
示例中第一次检测阳性和第二次测试阳性的联合概率 P(D1=1， D2=1）是否可以等于P(D1=1) * P(D2=1)？这两个事件的概率应该是相互独立的吧？
话说是13.06啦 
那患病的概率为什么不是 13.6% * 13.6% ~= 1.84% 捏
主要是概率论不是这么直观的想法啦，如果按照你这么算，那就意味着测试次数越多反而越不准确咯 
，按道理来说也不应该是这样的吧。
你忽略了H（病人实际的身体情况）
准确的来解释一下为什么会出现这个错误吧
你的计算方式有点像 P(D1=1, D1=1| H=1)含义就是我在知道被检测对象已经确认是病人的情况下第一次和第二次测试都是阳性的概率
然而这里我们要算的是P(H=1|D1=1, D1=1)含义是我们测试了两次结果都是阳性，被测试对象真的是阳性的概率
希望这么解释能帮助到你 
我也是，不过后来逐行加上去运行就好了。。。
第三题：
B只依赖于A, C只依赖于B, 有：
因果链条： A → B → C → P(A,B,C)
因此，P(A,B,C) = P(A) P(B|A) P(C|B)
如果不对的话 拜托帮忙指正，万分感谢！ 
1 Like
由条件概率公式：P(A,B,C)=P（A,B）P(C|A,B)
又因为C只依赖于B，那么有P(C|A,B)=P(C|B),即C发不发生跟A没有关系；
同理，将P(A,B)用条件概率公式分解，那么就有P(A,B,C)=P(A)P(B|A)P(C|B)
2 Likes
根据因果链条： A → B → C
感觉P(A, B, C)可以理解为：事件A发生的概率 x 事件A发生条件下事件B发生的概率 x 事件B发生的条件下事件C发生的概率
最终简化为：P(A)P(B|A)P(C|B)
若不对，恳请大家指正，谢谢🙏
1 Like
我觉得按照这个写的是把两次D1当作独立事件了，那么为什么可以这么计算尼？在题目中D1和D2都没能按照独立事件来计算。
%matplotlib inline
import torch
from torch.distributions import multinomial
from d2l import torch as d2l
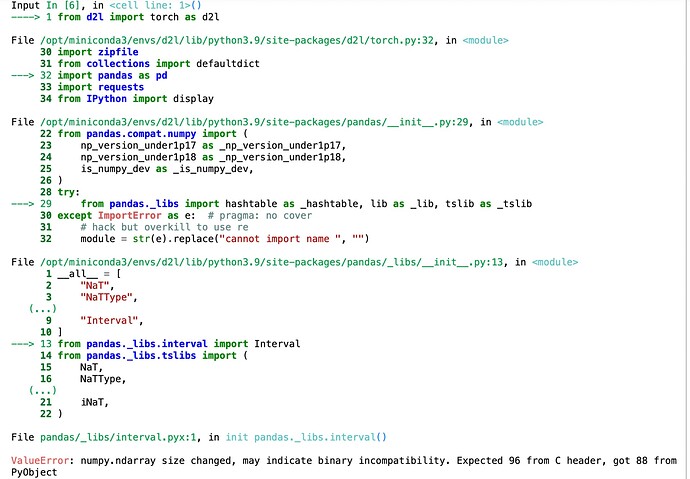
换成了d2l的内核，但是会一直出现No module named ‘torchvision’，不知道该如何解决这个问题
ModuleNotFoundError Traceback (most recent call last)
Input In [2], in <cell line: 4>()
2 import torch
3 from torch.distributions import multinomial
----> 4 from d2l import torch as d2l
File /Applications/anaconda3/envs/limu_d2l/lib/python3.8/site-packages/d2l/torch.py:6, in
4 import numpy as np
5 import torch
----> 6 import torchvision
7 from PIL import Image
8 from torch import nn
ModuleNotFoundError: No module named ‘torchvision’
请问一下你解决了吗？我也有一样的问题，如果解决的话麻烦告诉我一下谢谢啦