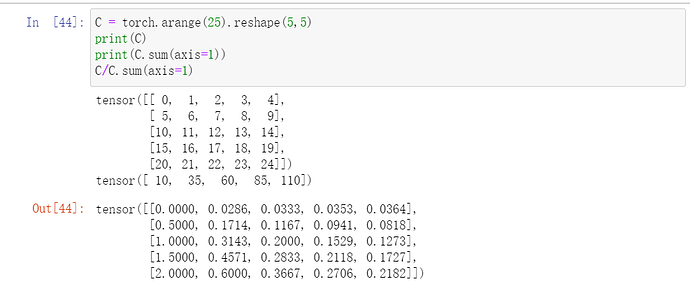
好勒,非常感谢道友的知识分享! 
C.sum(axis=2)很好理解。但是要计算C.sum(axis=0)时,可以写出C[0],C[1],用C[0]+C[1]。这是个人理解。但是碰到axis=1的时候,这种方法理解起来又出现了新的问题。比入到底应该 C[0][0]+C[0][1]+C[0][2];还是应该 C[0][0]+C[0][1]+C[0][2]+ C[1][0]+C[1][1]+C[1][2]。
对于大于等于三维的张量,不同维度的相加有没有更好的理解方法??
有了新的理解。C.sum(axis=1)就是找到C的第二维的数据,如果该维度的数值是3,那么就把第二维的数据3个3个加在一起。同理其他维度也是如此。
如果有更简单的理解方法请大神们指教!
这个地方的axis=0我理解的就是让0这个维度消失,也就是让行消失,按列来进行求和
tips:
1.还是建议在学习之前把整个知识点绘图为思维导图
2.对于学习是很容易忘记的,确定要进入该行业,对于知识点在大脑清晰的脉络还是非常importance
3.This is perfect deep learn’s book ,I have interesting in dl field
axis=0 ,可以理解为按行的方向进行压缩,那么就等价于按列求和,axis=1 理解为按列的方向进行压缩。不过如果维度过多axis=2,3这种,就不太好等价为按什么进行求和了
翻了翻文档才明白shape右对齐是将两个shape摆在一起,如下:
(4,3)
(3)
特意将3对齐,剩下的4为多出来的维度叫“头部维度”?只有3那列为“尾部维度”?尾部维度相同可以广播
Python里axis=0,是指运算沿着 ↓ 方向(向下)进行的;
axis=1,是指运算沿着 → 方向(向右)进行的。
拿sum函数举例,sum(axis=0)的结果就是把每一列求和再呈现出来,
sum(axis=1)的结果就是把每一行求和;
加上参数keepdims=True会更清晰
1,2,3:用线性代数证明。
4.答:输出是2。
5.答:是的。对应于形状中第一个轴的长度。
6.答:发生错误,因为形状不符合广播机制。广播机制是从形状尾部开始进行匹配,因此如果是A/A.sum(axis=1, keepdim=True),此时两者形状为(5, 4)和(5, 1),可以进行广播。
7.答:分别在轴0,1,2上降维,形状分别为(3, 4)、(2, 4)、(2, 3)。
8.答:均为一个标量。
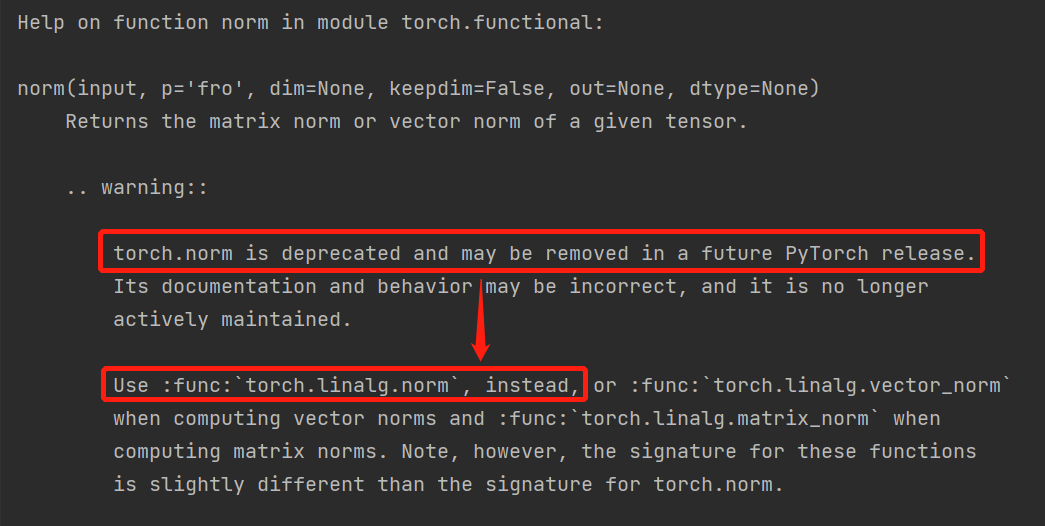
一点发现:2.3.10中的范数计算函数使用的是torch.norm(),但是在2.3.13的练习第8题中使用的是torch.linalg.norm()。建议统一采用torch.linalg.norm()。理由是通过查看torch.norm()官方文档说明(运行help(torch.norm)),发现torch.norm已经过时并可能在未来PyTorch版本中被移除,官方建议采用替代采用torch.linalg.norm,具体信息如下图所示:
0代表行的维度“消失了”,故只剩下一行,也就是列和;
1代表列的维度“消失了”,故只剩下一列,也就是行和;
为什么0代表方向,1代表类方向?
因为(m,n)表示m行n列,而这个二元坐标里,第0个元素代表行,第1个元素代表列。同理,三维张量坐标同理,在三元坐标(a,m,n),此时行方向应该是1,列方向应该是2
大佬你好,想知道笔记是怎么做的,非常美观欸
长度不匹配所以无法广播,可以看之前广播机制的原则,会发现A是方阵满足,右对齐,大小一致,不是方阵由于是对axis=1求和,再右对齐(axis=0和axis=1)大小必然不同,所以会报错,如果A/A.sum(axis=[0])不管A是什么形状都可以满足广播
你可以理解成最后求和之后消失的维度,比如axis=1就是维度为1会消失,书上没问题
行列相等的话,是ok的。A.sum(axis = 1)会使得轴1坍缩,当轴0和轴1的长度不同,是没法计算的。
行列相等时,可以根据上一节讲的广播进行运算。
其实可以总结广播的条件是:
看形状,轴数相等,且每个对应轴的长度相等或=1
另外一提,pytorch在进行矩阵乘法时除了可以用torch.mm(A, B)外,还可以A @ B,后面这种写法比较少见,但是简洁。
In [24]: A
Out[24]:
tensor([[ 0., 1., 2., 3.],
[ 4., 5., 6., 7.],
[ 8., 9., 10., 11.],
[12., 13., 14., 15.],
[16., 17., 18., 19.]])
In [25]: B
Out[25]:
tensor([[1., 1., 1.],
[1., 1., 1.],
[1., 1., 1.],
[1., 1., 1.]])
In [26]: torch.mm(A, B)
Out[26]:
tensor([[ 6., 6., 6.],
[22., 22., 22.],
[38., 38., 38.],
[54., 54., 54.],
[70., 70., 70.]])
In [27]: A @ B
Out[27]:
tensor([[ 6., 6., 6.],
[22., 22., 22.],
[38., 38., 38.],
[54., 54., 54.],
[70., 70., 70.]])
1.使用数学方法证明A = (A’)’ 即可,比较简单,不重复赘述
2.同上,使用数学方法证明 (A + B)’ = A’ + B’即可
3.同上,对于n*n方阵中的任一下标i,j元素,都可证明 Aij + Aji = Aij + Aji = Bij = Bji。其中B = A + A’
4.len(X)输出的是2
5.与4相同,一起解释。假设X为四维张量,当张量X 的shape为 m * n * q * l 时,len(X)的长度为m,对应dim=0的长度,即shape[0]的大小
6.运行 A/A.sum(axis=1) 会报错,报错原因如下:
假设A是shape为 m * n * q 的三维张量
则A.sum(axis=1)的 shape 为 m * q 的二维张量
我们知道,进行/运算时,要保证shape的大小是一致的,所以上式在运行时报错。
7. shape为(2,3,4)的形状,在dim=0时的输出shape为 (3,4),在dim=1时的输出shape为(2,4),在dim=2时的输出shape为(2,3)
8.提供一个四维的张量,经计算,输出的是一个标量,为L2范数,如下例子证明:

import torch
# x = torch.tensor(2.0)
# y = torch.tensor(3.0)
# print("x==y", x == y)
# y = x.clone()
# print("a copy to b", y)
# print("x*y", torch.mul(x, y), x * y)
# print("x/y", torch.div(x, y), x / y)
# print("x+y", torch.add(x, y), x + y)
# print("x**y", torch.pow(x, y), x ** y)
#
# print(torch.arange(4))
# print(torch.arange(16).view(2, 2, 4))
# print("--")
# x = torch.randn(2, 2)
# print("x value is ", x)
# print("x.sum to size to 1", x.sum(axis=[0, 1]), x.sum(axis=[1, 0]))
# print("--")
# print(x[1], len(x), x.shape, x.T)
#
# print(torch.arange(20).reshape(4, 5), torch.arange(20).view(1, 20))
# print("--")
# u = torch.tensor([3.0, -3.0])
# print(torch.norm(u))
def test_demo1():
print("test demo first")
x = torch.randn(2, 2)
y = x.clone()
print(x)
print("copy x to y ", y)
x = x.reshape(1, 4).reshape(2, 2)
print("x.reshape.reshape valuw same ?", x == y)
def test_demo2():
print("test demo second")
x, y = torch.randn(2, 2), torch.randn(2, 2)
print(f"x value is \n{x}\n\ny value is \n{y}\n")
_sum = torch.add(x, y)
print("x add y value is\n", _sum)
_sum2 = _sum.view(1, 4).view(1, 4)
print("sum value is same ?\n", _sum2 == torch.add(x.view(1, 4), y.view(1, 4)))
def test_demo3():
"""
如果矩阵 a 是对称的,则矩阵 a^T + a 也一定是对称的。但如果矩阵 a 不对称,那么矩阵 a^ T + a 就一般不是对称的。
"""
print("test demo third")
x = torch.randn(1, 5)
y = x.view(5, 1)
print(f"the sum value is\n {torch.add(x, y).numpy()}")
def test_demo4():
print("test demo forth")
x = torch.randn(2, 3, 4)
print("x value is\n", x)
print("x len is \n", len(x))
def test_demo5():
print("test demo 5")
x = torch.randn(3, 3)
print(f"x value is \n{x.numpy()}\nlen(x) value is\n {len(x)}")
def test_demo6():
print("test demo 6")
x = torch.randn(2, 2)
print(x)
print(f"a/a value is\n{x/x}\n{torch.div(x, x)}")
print(f"\n\n{'-'*50}\nsum(axis=1) value is\n{x.sum(axis=1)}")
def test_demo7():
"""
则输出结果将是一个标量,即形状为 ()。在 PyTorch 中,可以使用 dim 参数指定要沿着哪些轴进行求和,如果对所有的轴进行求和,则可以简单地写为 tensor.sum(),输出结果的形状为 ()。
如果只沿着某个轴进行求和,则输出结果形状中会减少对应的维度。例如,对轴 0 进行求和,则输出形状为 (3, 4);对轴 1 进行求和,则输出形状为 (2, 4);对轴 2 进行求和,则输出形状为 (2, 3)。
"""
print("test demo 7")
x = torch.randn(2, 3, 4)
print(x)
output = x.sum(dim=(0, 1, 2))
print(output)
def test_demo8():
"""
linalg.norm 函数可以接受一个张量,并计算它的范数(norm)。当张量具有多个轴时,我们可以通过指定 dim 参数来计算沿着哪些轴的范数。例如,对于一个大小为 (2, 3, 4) 的张量,我们可以按如下方式计算它的范数:
总结:
linalg.norm 函数可以用于计算一个张量的范数,无论它具有多少个轴。当我们指定了轴时,函数会返回沿着指定轴计算得到的范数,输出形状会从张量中移除对应的轴。如果没有指定轴,则函数对整个张量进行计算,输出结果是一个标量。
"""
x = torch.randn(2, 3, 4)
print(x)
# 沿着轴 (0, 1) 计算二范数:沿着轴 (0, 1) 计算了张量的二范数,输出结果是在两个轴上计算的范数,因此输出形状为 (4,)。
print(torch.linalg.norm(x, ord=2, dim=(0, 1)))
# 沿着轴 0 计算二范数:沿着轴 0 计算了二范数,这时会对轴 1 和 2 上的元素进行计算,输出形状为 (3, 4)。
print(torch.linalg.norm(x, ord=2, dim=0))
# 对整个张量计算二范数:没有指定任何轴,因此函数对整个张量进行了计算,输出结果是一个标量。
print(torch.linalg.norm(x))
if __name__ == '__main__':
test_demo8()
test_demo7()
test_demo6()
test_demo5()
test_demo4()
test_demo3()
test_demo2()
test_demo1()
运行结果
tensor([[[-1.2545, -0.5056, 1.3154, -0.0660],
[ 1.0682, 0.3092, -0.9484, 0.9354],
[ 0.3330, 0.0151, -0.3165, -0.4617]],
[[-1.5198, 1.0027, -0.4004, -1.3944],
[ 1.3531, -0.2831, -0.7134, -0.5271],
[ 0.0807, 0.5723, 0.4047, 0.7291]]])
tensor([2.6324, 1.2934, 1.6523, 1.7419])
tensor([[1.9707, 1.1229, 1.3750, 1.3960],
[1.7239, 0.4193, 1.1868, 1.0737],
[0.3426, 0.5725, 0.5138, 0.8630]])
tensor(4.0183)
test demo 7
tensor([[[-0.6596, 0.3917, -0.1141, -0.6916],
[ 0.6180, 1.3962, 0.9149, -0.6632],
[-0.2597, -1.3846, -1.8263, 0.3115]],
[[ 0.6879, 0.7319, -1.9681, 1.0238],
[-0.7598, 1.2949, 0.7910, 0.9299],
[ 0.5629, 1.0090, -0.0192, 0.1628]]])
tensor(2.4804)
test demo 6
tensor([[ 1.6858, -1.0559],
[-0.6865, -0.8169]])
a/a value is
tensor([[1., 1.],
[1., 1.]])
tensor([[1., 1.],
[1., 1.]])
--------------------------------------------------
sum(axis=1) value is
tensor([ 0.6298, -1.5034])
test demo 5
x value is
[[-0.24163365 -1.562805 0.32346362]
[-0.04694848 -0.15506767 -1.060381 ]
[-0.8978073 -0.04264306 0.2788014 ]]
len(x) value is
3
test demo forth
x value is
tensor([[[-0.3772, 0.1083, 1.0138, -1.2778],
[-1.3714, -1.6503, 1.6648, 0.8888],
[-0.6994, -1.5098, -0.4362, 0.4289]],
[[ 0.4660, -0.0861, 0.7674, -0.8659],
[ 1.4352, -0.2237, -0.2477, -0.2899],
[ 0.3212, -0.9914, -0.4831, 0.1442]]])
x len is
2
test demo third
the sum value is
[[ 1.3835357 -0.70508033 0.9173095 0.4717696 -0.22867692]
[-0.70508033 -2.7936964 -1.1713065 -1.6168464 -2.317293 ]
[ 0.9173095 -1.1713065 0.45108336 0.00554341 -0.69490314]
[ 0.4717696 -1.6168464 0.00554341 -0.43999654 -1.1404431 ]
[-0.22867692 -2.317293 -0.69490314 -1.1404431 -1.8408896 ]]
test demo second
x value is
tensor([[-2.0150, -0.8099],
[-0.1205, 0.3034]])
y value is
tensor([[ 0.5589, 0.0835],
[-0.0257, 0.8108]])
x add y value is
tensor([[-1.4561, -0.7264],
[-0.1462, 1.1142]])
sum value is same ?
tensor([[True, True, True, True]])
test demo first
tensor([[ 0.4403, -0.7769],
[ 1.2694, -1.1072]])
copy x to y tensor([[ 0.4403, -0.7769],
[ 1.2694, -1.1072]])
x.reshape.reshape valuw same ? tensor([[True, True],
[True, True]])