A @ B好像并不少见，而且一开始是由numpy最先使用的 A @ B，到后面python解释器版本，直接把这个用法内置了，也就是不用引入numpy，也可以直接使用 A @ B
axis是轴序号，按轴来理解比较好。降维实际上是选择一个轴，把这个轴给去掉，去掉的同时可以使用平均、求和等操作保留信息。自己扩展到3个轴，4个轴，看下sum、mean的行为是怎么样的就好理解了。
你是分别求的x的平均值和a的平均值，x和a是不是相等的？不等的话平均值不一样也很正常啊 。
可以这样理解，不如将 axis=？看作是从前开始数的第（？+1）个[ ，这样看上去更清晰一点，高维张量也是一样
axis=0 书上写对所有行操作，省去了一个前置：（对一列的）所有行进行操作。语文翻译引起了歧义
你好，请问是哪一个第7题？2.3线代这章好像没看到曼哈顿距离相关的题
-
证明一个矩阵𝐴的转置的转置是𝐴，即(𝐴⊤)⊤=𝐴。
相当于绕对角线旋转360度 -
给出两个矩阵𝐴和𝐵，证明“它们转置的和”等于“它们和的转置”，即𝐴⊤+𝐵⊤=(𝐴+𝐵)⊤。
因为Aij = ATji , Bij = BTji
所以ATji + BTji = Aji + Bji
(A+B)ij = Aij + Bij
(A+B)Tji = (A+B)ij = Aij + Bij = ATji + BTji -
给定任意方阵𝐴，𝐴+𝐴⊤总是对称的吗?为什么?
即证明(A+AT)T = A+AT
因为2 , (A+AT)T = AT + (AT)T
因为1 , (AT)T=A
所以(A+AT)T = AT + A = A + AT -
本节中定义了形状(2,3,4)的张量
X。len(X)的输出结果是什么？
2,len(X)返回第一个dimention长度. -
对于任意形状的张量
X,len(X)是否总是对应于X特定轴的长度?这个轴是什么?
第一个dimention的维数 -
运行
A/A.sum(axis=1)，看看会发生什么。请分析一下原因？
假如A = shape(4,3) , 那么 A.sum(axis=1).shape 是(4,), A/A.sum(axis=1) 报错,因为其最后一个dimention 4 不是1 ,无法完成广播.
假如A = shape(2,3,4),那么A.sum(axis=1).shape是(2,4),与(2,3,4)之间无法完成广播, 也是报错
假如A = shape(2,2,4),那么A.sum(axis=1).shape是(2,4),与(2,2,4)之间可以完成广播.但是这个除法的语义不对 -
考虑一个具有形状(2,3,4)的张量，在轴0、1、2上的求和输出是什么形状?
分别是(3,4),(2,4),(2,3) -
为
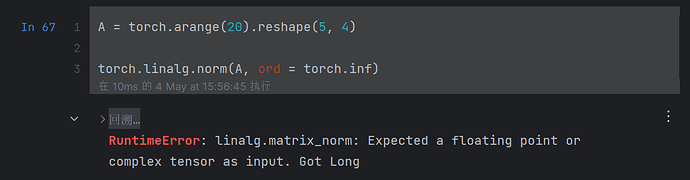
linalg.norm函数提供3个或更多轴的张量，并观察其输出。对于任意形状的张量这个函数计算得到什么?
torch.linalg.norm(torch.arange(20,dtype=torch.float32)) => 49.6991
torch.linalg.norm(torch.arange(20,dtype=torch.float32).reshape(5,2,2)) => 49.6991
不论shape, 都是得到所有元素的$\sqrt {\Sigma X^2}$
https://zh.d2l.ai/chapter_preliminaries/linear-algebra.html#id10
“ 我们可以把一个矩阵𝐴∈𝑅𝑚×𝑛乘法看作一个从𝑅𝑛到𝑅𝑚向量的转换”表述成
“把向量𝑥∈𝑅𝑛乘以𝐴∈𝑅𝑚×𝑛看作𝑥从𝑅𝑛到𝑅𝑚向量的转换”可能会更明了一些。
第2题的证明缜密点应该是设C=A + B，A、B、C的转置分别是D、E、F，那么有：
fji = cij = aij + bij = dji + eji
得证
- 对于轴或维，NumPy 中使用
axis，PyTorch 中使用dim； - 对于维度保持，NumPy 中使用
keepdims，PyTorch 中使用keepdim。
虽然它们在运行时是兼容的，但为了在 PyCharm 等 IDE 中有更好的代码提示体验，应规范这些参数的使用。
更具体地，是将目标函数（这里是 sum()）作用在的维度 dim=0 上。目标函数恰巧可以实现降维。
我是这样记忆的。
背景知识：
- “列”是向量的默认方向；
- 矩阵是向量的容器，二维矩阵的每列都可视为向量；
于是，0 维（dim=0）表示向量的每个元素所在方向，1 维（dim=1）表示矩阵的每个元素（即，向量）所在方向，以此类推。
hw 1-3在论坛不太好表示，一种简单的证明方法是跟踪每个元素a_ij经过转置运算或者其它运算后的位置变化，或者在计算机中随机生成一个tensor以证明，正规的证明方式是借助辅助符号，改天补上（肚子好饿
# homework 4
x = torch.arange(24).reshape(2, 3, 4)
len(x)
# output is 2
# hw 5
x = torch.arange(24).reshape(4, 6)
len(x)
# 是的，经过样例，作业4和作业5我的试验，发现至少对于1，2，3维的tensor都是如此
# hw 6
A, A.sum(dim=1) # error: A/A.sum(dim=1) : The size of tensor a (4) must match the size of tensor b (5) at non-singleton dimension 1
# 根据报错信息，在维度1（从0开始），第二个tensor维度比第一个tensor的维度大（递增了），导致错误，第一个tensor是5*4的，第二个是1*5的，都是二维tensor，可能在这种情况下无法使用广播机制
# hw 7
x = torch.arange(24).reshape(2, 3, 4)
x, x.sum(dim=0).shape, x.sum(dim=0), x.sum(dim=1).shape, x.sum(dim=1), x.sum(dim=2).shape, x.sum(dim=2)
# dim 0: 3 * 4; dim 1: 2 * 4; dim 2: 2 * 3
# 理解：沿着哪个dim，就把这个dim方向上的数加在一起拍扁，并且维数也降了一维，可以画图理解
# hw 8
import numpy
numpy.linalg.norm(x), torch.sqrt(torch.sum(x * x))
# 对比发现，类似于二维矩阵的2-范数，这是tensor的2-范数
我的理解 axis=0 就是把最外层的看成一个向量，axis=1 级别的都设成一个变量 x
[x1,x2,…xn],
axis=1 就是把第二层数组内的元素看成一个变量
[
[x11, x12, …x1n],
[x21, x22, …x2n],
]
x可以是标量或者任意张量
以此类推
A/A.sum(axis=1)怎么才能广播，使其可以进行计算呢
交作业：
import torch
1.证明一个矩阵的转置的转置是原矩阵
A = torch.arange(20).reshape(5, 4)
print(“Original matrix A:”)
print(A)
print(“\nTranspose of A (A.T):”)
print(A.T)
print(“\nTranspose of the transpose of A (A.T.T):”)
print(A.T.T)
验证 A 是否等于 A.T.T
print(“\nIs A equal to A.T.T?”)
print(A == A.T.T)
2.给定两个矩阵A和B，证明“它们转置的和”等于“它们和的转置”
B = torch.tensor([[1, 5, 6, 7], [2, 3, 4, 8], [7, 6, 5, 4], [3, 2, 1, 0], [9, 8, 7, 6]])
print(A.T + B.T == (A + B).T)
3.给定任意方阵，总是对称的吗?为什么?
A = torch.arange(25).reshape(5, 5)
A = torch.arange(16).reshape(4, 4)
print(A + A.T)
4.本节中定义了形状(2, 3, 4)的张量X。len(X)的输出结果是什么？
X = torch.arange(24).reshape(2, 3, 4)
print(X,‘\n’,len(X)) #2
5.对于任意形状的张量X，len(X)是否总是对应于X特定轴的长度?这个轴是什么?
X = torch.arange(72).reshape(6, 3, 4)
print(X,‘\n’,len(X)) #它返回的是张量的第一个维度的大小，即6
6.运行A/A.sum(axis=1)，看看会发生什么。请分析一下原因？
print(A,‘\n’,A.sum(axis=1),‘\n’,A/A.sum(axis=1))
发生了广播机制，A.sum(axis=1)的结果是一个形状为(5,)的向量，而A的每一行都与这个向量做了按元素相除运算
7.考虑一个具有形状(2, 3, 4)的张量，在轴0、1、2上的求和输出是什么形状?
print(X)
print(X.sum(axis=0),‘\n’,X.sum(axis=0).shape,‘\n’,X.sum(axis=1),‘\n’,X.sum(axis=1).shape,‘\n’,X.sum(axis=2),‘\n’,X.sum(axis=2).shape)
(3, 4) (2, 4) (2, 3)
8.为linalg.norm函数提供3个或更多轴的张量，并观察其输出。对于任意形状的张量这个函数计算得到什么?
X = X.float()
print(torch.linalg.norm(X))
创建一个具有形状 (2, 3, 4) 的张量
X = torch.arange(24).reshape(2, 3, 4).float()
X = torch.arange(120).reshape(2, 3, 5, 4).float()
打印张量 X
print(“Tensor X:”)
print(X)
计算并打印张量 X 的范数
norm_X = torch.linalg.norm(X)
print(“\nNorm of tensor X:”)
print(norm_X)
函数默认计算的是 Frobenius 范数，这与张量的轴数无关。
Frobenius 范数是所有元素的平方和的平方根。无论张量有多少个轴，计算方法都是一样的
若有错误，希望大家指正。
我的是 A.mean()报错mean(): could not infer output dtype. Input dtype must be either a floating
好像现在 mean 只能处理 float 类型 or complex dtype，要改成 float 才能运行