Predicting House Prices on Kaggle

[mli]

http://d2l.ai/chapter_multilayer-perceptrons/kaggle-house-price.html

[pr2tik1]

If we add hidden layers and non-linearity, will it be still linear regression? Why does the MLP with hidden layer performs good on “linear regression” ?

[goldpiggy]

Hey @pr2tik1, it won’t be linear regression if we add non-linearity, but statistically we called “logistic regression” a “generalized linear model” since its outputs depend on a linear combinations of model parameters (beta’s), rather than products of quotients.

[pr2tik1]

Thanks for reply @goldpiggy !

[pr2tik1]

I also have doubt regarding the normalization of the values. Here the target variable SalePrice is also normalized, which makes its values range from about (-5,5). While submitting predictions to Kaggle what step is taken to get back the range of desired SalePrice values [like 10,000, 20,000]?

[goldpiggy]

SalePrice is the label, and we are not normalizing the label values.

[MorrisXu-Driving]

There is a bug in the train_and_pred() function. test_data[‘SalePrice’] = pd.Series(preds.reshape(1, -1)[0]) only return the first prediction. To correct the error, we need to first flatten the ‘preds’ by adding .flatten() after the numpy() and delete the ‘.reshape(1, -1)[0]’

[goldpiggy]

Hi @MorrisXu-Driving, thanks for your suggestion!

I agree that flatten() is a more elegant way, while it seems like these methods have equivalent results. Any other bug exists here?

[Dchaoqun]

As far as I understood, the model should have no knowledge of the test data. Therefore,
for data preprocessing, shouldn’t we use only the training data to calculate the mean and variance,
then use them to rescale the test data?

[goldpiggy]

Hi @Dchaoqun, great question! The normalization step here is to have all the features in the same scales, rather than one feature in range [0,0.1], another in [-1000, 1000]. The later case may lead to some sensitive weights parameters. But you are right, in the real life scenario, we may not know the test data at all, so we will assume the test and train set are following the similar feature distributions.

[Dchaoqun]

Hi @goldpiggy, thank you for the clarification!

[S_X]

Hi @goldpiggy,
In the train function, why is MSEloss used as the loss function instead of log_rmse?

[goldpiggy]

Hey @S_X, good question! That’s why we leave it as an exercise in question 2.

[Andong]

I guess,maybe the gradient will be too small due to the derivation of (log(y)-log(y hat))^2.I don’t know if I am right.

[Nish]

A minor point, but in the PyTorch definition of log_rmse :

def log_rmse(net, features, labels):
    # To further stabilize the value when the logarithm is taken, set the
    # value less than 1 as 1
    clipped_preds = torch.clamp(net(features), 1, float('inf'))
    rmse = torch.sqrt(torch.mean(loss(torch.log(clipped_preds),
                                       torch.log(labels))))
    return rmse.item()

Isn’t the torch.mean() call unnecessary, since loss is already the Mean Squared Error, ie the mean is already taken?

[Nish]

I tried to predict the logs of the prices instead, using the following loss function:

def log_train(preds, labels):
    clipped_preds = torch.clamp(preds, 1, float('inf'))
    rmse = torch.mean((torch.log(clipped_preds) - torch.log(labels)) ** 2)
    return rmse

And the results were much worse. During the k-fold validation step, some of the folds had much higher validation/training losses than the others:

And sometimes the plot of losses didn’t appear to descend with epochs at all:

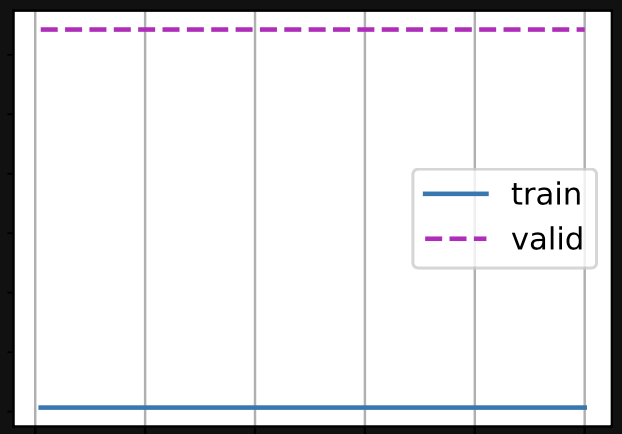
I suppose this is the point of the exercise, to show that it’s a bad idea, but I’m having trouble understanding why. It seems that instead of trying to minimise some concept of absolute error we’re trying to minimise a concept of relative (percentage) error between the prediction and the reality. Why would this lead to such instability?

Edit: I have an idea. In order to maintain numerical stability we have to clamp the predictions:

clipped_preds = torch.clamp(preds, 1, float('inf'))

But if the network parameters are initialised so that all of the initial predictions are below 1 (as is what I observed debugging one run) then they could all get clamped in this way and backprop would fail as the gradients are zero/meaningless?

[goldpiggy]

@Nish

I suppose this is the point of the exercise, to show that it’s a bad idea, but I’m having trouble understanding why. It seems that instead of trying to minimise some concept of absolute error we’re trying to minimise a concept of relative (percentage) error between the prediction and the reality. Why would this lead to such instability?

Hey @Nish, great question! Actually using log_rmse may not be a bad idea. I guess you only change the loss function but not other hyperparameters such as “lr” and “epoch”. Try a smaller “lr” such as 1, and a larger “epoch” such as 1000. What is more, the folds with high loss as 12 here might result from bad initialization, you can try net.initialize(init=init.Xavier() and more details here.)

[Nish]

Thank you @goldpiggy ! So it sounds like my final point could be correct - that the issues came from bad initialisation so that all the initial predictions get clamped to 1 and the gradient is meaningless?

[goldpiggy]

Hey @Nish, you got the idea! Initialization and learning rate are crucial to neural network. If you read further into advanced HPO in later chapters, you will find learning rate scheduler. Keep up!

[StevenJokes]

Hi， @goldpiggy

Analogy：

• Initialization is more like talent?
• lr is more like efforts to understand world?