Please check https://github.com/d2l-ai/d2l-en/issues/1141 quickly, I think it maybe makes all eval wrong.
How do we judge whether $a$ is a function of $b$ or not?
Or we just judge by that we haven’t defined it before, rather than whether $a$ has a relationship with $b$ in reality or not.
Hi @StevenJokes, $y$ is the true label, while $\hat{y}$ is the estimated label. Hence $\hat{y}$ is a function of $o$, while $y$ is not.
I already have understand $y_j$ is the true label, such as one-hot. But the diverce of our thinking is that I think the true label has a certain relationship with $o_j$, so I think $y_j$ is also $o_j$'s function. When we get same $o_j$, we get only one and $y_j$. Doesn’t it conform the defination of function.
But the function is discrete.
As we saw in “Freshness and Distribution Shift”, if production data is different from the data a model was trained on, a model may struggle to perform. To help with this, you should check the inputs to your pipeline.
In 10. Build Safeguards for Models - Building Machine Learning Powered Applications [Book]
Although softmax is a nonlinear function, the outputs of softmax regression are still determined by an affine transformation of input features; thus, softmax regression is a linear model.
Can anyone explain this why is it so? because when we say that a model is linear model , then it means model is linear in the parameter but in softmax regression , we are applying softmax function which is non linear so our model parameter will become non linear.
Just a statistical speaking!
1 Like
exercise 1.1
apparrently i copied the answer above, 1.2 the variance is a vector and the j-th element is exactly the form of above which is softmax(0)_j(1-softmax(0)_j)
exercise 3.3 use the squeeze theorem and it’s easy to prove
3.4 softmin could be softmin(-x)? i dont know
3.5 pass (too hard to type on the computer)
In formula 3.4.7,
I couldn’t understand why the later 2 equations are equal, could someone explain a bit more to me? Thanks.
Hi @Gavin, great question. A simple answer is:
For more details, please check 22.7. Maximum Likelihood — Dive into Deep Learning 1.0.3 documentation
@goldpiggy
The simple answer seems to be Tautology.
I have read URL you give.
But I think it didn’t solve this question.
I can’t find anything in it.
?
Hello. I am still not able to understand clearly how these 2 equations are related. Can you please explain, how for a particular observation i, the probability y given x is related to the entropy definition overall classes?
Thank you for your response. My question was more specifically why
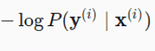is same as
l(y,y_hat)
Is this because y when 1-hot encoded has only single position with 1 and hence when we sum up the y * log(y_hat) over the entire class, we are left with the probability y_hat corresponding to true y. Please advise.
@Abinash_Sahu
l (y，y _ hat)
Cross entropy loss
Only one type of these losses we often use.
https://ml-cheatsheet.readthedocs.io/en/latest/loss_functions.html
Q1.2. Compute the variance of the distribution given by softmax(𝐨)softmax(o) and show that it matches the second derivative computed above.
Can someone point me in the right direction? I tried to use Var[𝑋]=𝐸[(𝑋−𝐸[𝑋])^2]=𝐸[𝑋^2]−𝐸[𝑋]^2 to find the variance but I ended up having the term 1/q^2… it doesn’t look like the second derivative from Q1.1.
Thanks!
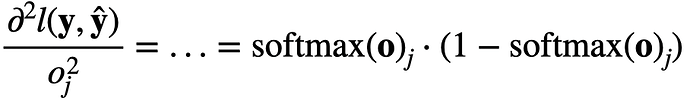
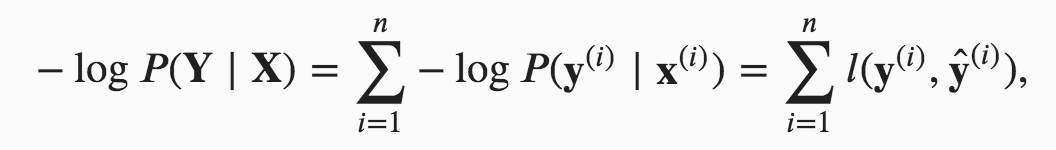
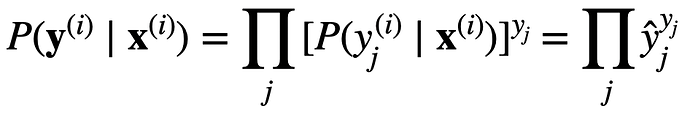
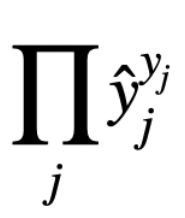
1 Like