网络中的网络（NiN）

中文版 pytorch
30

网上有个对于用两个1*1卷积的解释：第一个1x1卷积层实现featuremap的提取，第二个1x1卷积层进行featuremap的组合，但是不清楚对不对

31

image
image1168×622 44.9 KB

两个1x1卷积
image
image1173×579 45.8 KB

去掉一个1x1卷积
这也差太多了吧！

1 Like
32

画图时出现该报错
ValueError: svg is not a valid value for output; supported values are path , agg , macosx site:stackoverflow.com
可能需要修改

33

最后一层并没有添加softmax函数啊，最后一层只是用flatten展平了啊

34

hi，我也遇到了同样的问题，我觉得可能是网络初始化的问题，于是我试着重新初始化了net，发现是可行的

35

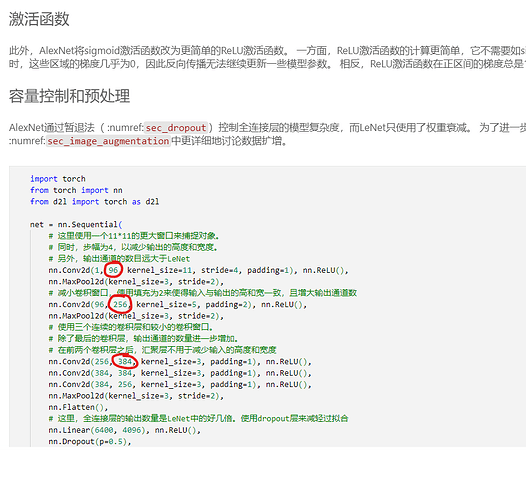
请问怎么选择卷积中的stride和padding呢？

36

按照计算（224+2乘以padding-11）/4+1，前面如何都算不出整数，有小数，就不知道内部怎么计算，答案是54。
padding=1，算出来54.75
padding=0，算出来54.25
个人觉得不用，因为最后都有多的行，1和0都可以

37

哥，你知不知道你在说啥，每个1x1是参数有1x96x54x54=279,936，一个参数的话我为什么要这一层，删了不就行了

38

调整NiN的超参数，以提高分类准确性。

依旧使用SGD，学习率调为0.12， epoch 15

epoch: 0 loss= 949.5301513671875

epoch: 1 loss= 541.0523071289062

epoch: 2 loss= 335.288818359375

epoch: 3 loss= 265.7752990722656

epoch: 4 loss= 236.0061492919922

epoch: 5 loss= 214.9103546142578

epoch: 6 loss= 200.35089111328125

epoch: 7 loss= 186.38710021972656

epoch: 8 loss= 173.8882293701172

epoch: 9 loss= 164.55499267578125

epoch: 10 loss= 157.58424377441406

epoch: 11 loss= 150.84255981445312

epoch: 12 loss= 145.72850036621094

epoch: 13 loss= 139.71893310546875

epoch: 14 loss= 134.76446533203125

测试集准确度 0.8855999708175659

为什么NiN块中有两个 1×1 卷积层？删除其中一个，然后观察和分析实验现象。


import numpy as np

import torch

import torchvision

import torchvision.transforms as transforms

import torch.nn as nn

import torch.nn.functional as F

import torch.optim as optim

import matplotlib.pyplot as plt

device = torch.device('cuda:0')

train_set = torchvision.datasets.FashionMNIST(

    root='./dataMnist'

    ,train=True

    ,download=True

    ,transform=transforms.Compose([

        transforms.ToTensor(),

        transforms.Resize((224, 224))

    ])

)

train_loader = torch.utils.data.DataLoader(

    train_set,

    batch_size=128,

    shuffle=True,

    num_workers = 0

)

test_set = torchvision.datasets.FashionMNIST(

    root='./dataMnist'

    ,train=False

    ,download=True

    ,transform=transforms.Compose([

        transforms.ToTensor(),

        transforms.Resize((224, 224))

    ])

)

test_loader = torch.utils.data.DataLoader(

    test_set,

    batch_size=128,

    shuffle=True,

    num_workers = 0

)

#创建Nin块

def Nin_block(in_channels, out_channels, padding, stride, kernel_size):

    return nn.Sequential(

        nn.Conv2d(in_channels, out_channels, padding=padding ,stride=stride, kernel_size=kernel_size),

        nn.ReLU(),

        nn.Conv2d(out_channels, out_channels, kernel_size=1),nn.ReLU(),

        nn.Conv2d(out_channels, out_channels, kernel_size=1), nn.ReLU()

    )

def Nin():

    return nn.Sequential(

        Nin_block(1, 96, stride=4, kernel_size=11, padding=0),

        nn.MaxPool2d(kernel_size=3, stride=2),

        Nin_block(96, 256, stride=1, kernel_size=5, padding=2),

        nn.MaxPool2d(kernel_size=3, stride=2),

        Nin_block(256, 384, stride=1, kernel_size=3, padding=1),

        nn.MaxPool2d(kernel_size=3, stride=2),

        nn.Dropout(0.5),

        Nin_block(384, 10, stride=1, kernel_size=3, padding=1),

        nn.AdaptiveAvgPool2d((1, 1)),

        nn.Flatten() #去掉多余的维数

    )

net = Nin()

# x = torch.zeros((1, 1, 224, 224))

# for layer in net:

#     x = layer(x)

#     print(layer.__class__.__name__, "\t输出的格式为: ", x.shape)

def init_weights(layer):

    if type(layer)== nn.Linear or type(layer) == nn.Conv2d:

        nn.init.xavier_uniform_(layer.weight)  #初始化很重要，NiN随机初始化训练不动。。。

net.apply(init_weights)

print("Nin的结构为:", net)

optimizer = optim.SGD(net.parameters(), lr = 0.1)

loss = nn.CrossEntropyLoss(reduction='mean')

epoch = 10

losses = []

for i in range(epoch):

    loss_sum = 0

    for x, y  in train_loader:

        net = net.to(device)

        x = x.to(device)

        y = y.to(device)

        y_hat = net(x)

        loss_temp = loss(y_hat, y)

        loss_sum += loss_temp

        optimizer.zero_grad()

        loss_temp.backward()

        optimizer.step()

    losses.append(loss_sum.cpu().detach().numpy()/train_set.data.shape[0])

    print("epoch: ",i, "loss=", loss_sum.item())

acc = 0

with torch.no_grad():

    for x, y in test_loader:

        x = x.to(device)

        y = y.to(device)

        y_hat = net(x)

        acc += torch.sum(y_hat.argmax(dim=1).type(y.dtype) == y)

    print("测试集准确度",(acc/test_set.data.shape[0]).item())

plt.plot(range(epoch), losses)

plt.xlabel('epoch')

plt.ylabel('loss')

plt.show()



epoch:  0 loss= 993.8709716796875

epoch:  1 loss= 533.2142944335938

epoch:  2 loss= 361.1051330566406

epoch:  3 loss= 277.5993347167969

epoch:  4 loss= 232.45095825195312

epoch:  5 loss= 205.37686157226562

epoch:  6 loss= 187.60452270507812

epoch:  7 loss= 176.19105529785156

epoch:  8 loss= 165.3572540283203

epoch:  9 loss= 157.9745330810547

测试集准确度 0.8700000047683716

俩个可以多次融合通道信息

换成一个：


Nin的结构为: Sequential(

  (0): Sequential(

    (0): Conv2d(1, 96, kernel_size=(11, 11), stride=(4, 4))

    (1): ReLU()

    (2): Conv2d(96, 96, kernel_size=(1, 1), stride=(1, 1))

    (3): ReLU()

  )

  (1): MaxPool2d(kernel_size=3, stride=2, padding=0, dilation=1, ceil_mode=False)

  (2): Sequential(

    (0): Conv2d(96, 256, kernel_size=(5, 5), stride=(1, 1), padding=(2, 2))

    (1): ReLU()

    (2): Conv2d(256, 256, kernel_size=(1, 1), stride=(1, 1))

    (3): ReLU()

  )

  (3): MaxPool2d(kernel_size=3, stride=2, padding=0, dilation=1, ceil_mode=False)

  (4): Sequential(

    (0): Conv2d(256, 384, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))

    (1): ReLU()

    (2): Conv2d(384, 384, kernel_size=(1, 1), stride=(1, 1))

    (3): ReLU()

  )

  (5): MaxPool2d(kernel_size=3, stride=2, padding=0, dilation=1, ceil_mode=False)

  (6): Dropout(p=0.5, inplace=False)

  (7): Sequential(

    (0): Conv2d(384, 10, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))

    (1): ReLU()

    (2): Conv2d(10, 10, kernel_size=(1, 1), stride=(1, 1))

    (3): ReLU()

  )

  (8): AdaptiveAvgPool2d(output_size=(1, 1))

  (9): Flatten(start_dim=1, end_dim=-1)

)

epoch:  0 loss= 847.5736694335938

epoch:  1 loss= 356.9827575683594

epoch:  2 loss= 261.1847839355469

epoch:  3 loss= 224.17762756347656

epoch:  4 loss= 196.07040405273438

epoch:  5 loss= 180.1049041748047

epoch:  6 loss= 171.22512817382812

epoch:  7 loss= 160.30470275878906

epoch:  8 loss= 153.3402099609375

epoch:  9 loss= 147.3529052734375

测试集准确度 0.8526999950408936

换成一个效果略低，俩个可以增加模型的非线性表达能力。

计算NiN的资源使用情况。参数的数量是多少？计算量是多少？

参数$96(11111+1)+(119696)2+256(9655+1)+(11256256)2+384(25633+1)+(11384384)2+10(38433+1)+2(1110*10)=1995284$

计算量:
$(5454961111)+(5454969696)2+(262625655)+(2626256256256)2+(121238433)+(1212384384384)+(103845533)+(105510*10)2 = 2.46910^{10}$

一次性直接将 384×5×5 的表示缩减为 10×5×5 的表示，会存在哪些问题？

信息损失过大？

2 Likes
39

感觉文章中的logtis翻译成预估比较好吧

40

optimizer, lr, num_epochs, batch_size, resize = adam, 0.001, 10, 512, 96
epoch 10, loss 0.234, train acc 0.913, test acc 0.906

optimizer, lr, num_epochs, batch_size, resize = adam, 0.002, 10, 1024, 96
epoch 10, loss 0.241, train acc 0.912, test acc 0.901

41

这是什么情况？Train_loss不稳定波动
lr=0.1 batchsize=128 epochs=10
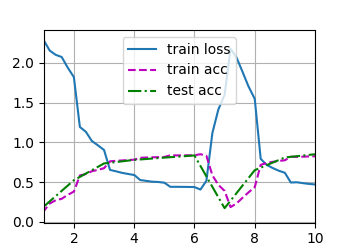
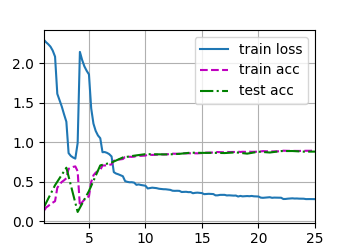
image

42

image
这是我 lr=0.03 batch_size=128 epochs=25的结果，同样出现了Loss和Acc的波动。有人能解释一下为什么吗？>.<

43

训练集loss逐渐下降，然后loss反而增大。这不是过拟合，因为过拟合时，train_loss仍然是下降的。这种情况是网络退化。残差网络ResNet 可以解决这一问题。

44

是不是学习率爆炸啊，当学习率设置过大时，每次参数更新的步长也会变得很大，可能会导致在损失函数的表面上来回震荡，无法收敛到最小点。甚至在极端情况下，参数更新的步长可能足够大，使得损失函数的值越来越大，使得模型发散。

45

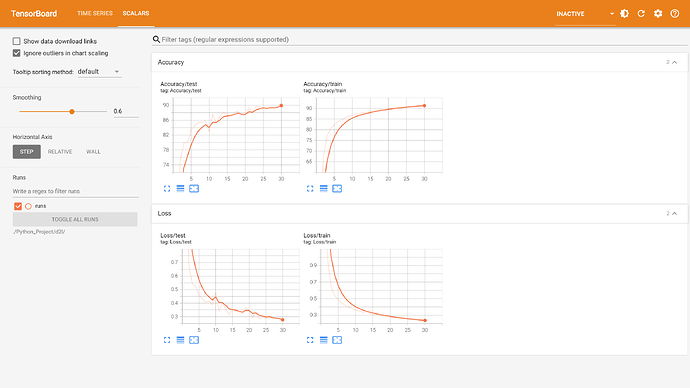
在Q2中，我减小了NiN块的一个卷积层，然后调参，准确率达到90%以上。

net = nn.Sequential(
    nin_block(1, 96, kernel_size=11, strides=4, padding=0),
    nn.MaxPool2d(3, stride=2),
    nin_block(96, 256, kernel_size=5, strides=1, padding=2),
    nn.MaxPool2d(3, stride=2),
    nin_block(256, 256, kernel_size=3, strides=1, padding=1),
    nn.MaxPool2d(3, stride=2),
    nn.Dropout(0.5),
    # 标签类别数是10
    nin_block(256, 10, kernel_size=3, strides=1, padding=1),
    nn.AdaptiveAvgPool2d((1, 1)),
    # 将四维的输出转成二维的输出，其形状为(批量大小,10)
    nn.Flatten())

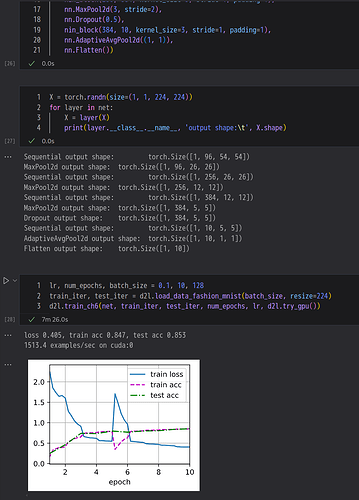
lr, num_epochs, batch_size = 0.04, 30, 128
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size, resize=224)
d2l.train_ch6(net, train_iter, test_iter, num_epochs, lr, d2l.try_gpu())

结果是：
loss 0.239, train acc 0.911, test acc 0.909
3530.1 examples/sec on cuda:0

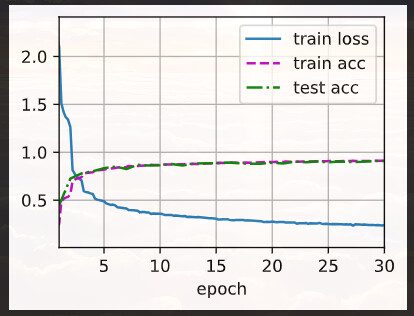
image

46

在我的电子书里，AlexNet输出通道确实是96, 256, 384, 10。你说的64, 128, 256, 512，是VGG的通道数设置吧。

屏幕截图 2024-04-20 114925
屏幕截图 2024-04-20 114925876×832 54.2 KB

47

我有个疑问是您的前一个回答“原始的NiN模型对于这个数据集过于复杂了”，模型复杂的意思本身似乎就是参数量很大？这样的话，那过于复杂是不是就是说过拟合了。。
我个人对2个1x1没有1个1x1效果好的看法是：
首先不是过拟合，因为（1）像您说的train&test acc没有显著差异，说明没有出现过拟合；（2）1x1的卷积核的参数量是in_chxout_ch，对256来说也就是60k的数量级，相比网络本身不算很大，所以加上1层应该不会让模型变得过于复杂？
我觉得几层1x1就是一个工程的问题：神经网络是一门语言，用来描述数据集蕴含的特征信息（引自沐神），对ImageNet来说2层1x1更好地提取描述像素的非线性，对Fashion-MNIST来说1层更好。我们只知道“1x1层数和数据集有关”，具体几层，试一试就完了 :joy:

48

图片
图片964×1340 137 KB

这种train acc暴跌是为什么？

49

若没有显式地初始化，对于示例所用的简单数据集而言，NiN 作为较深的模型而难以训练。于是，使用 nn.init.kaiming_normal_() 方法的 Kaiming 正态分布初始化权重。

image
image2560×1440 220 KB