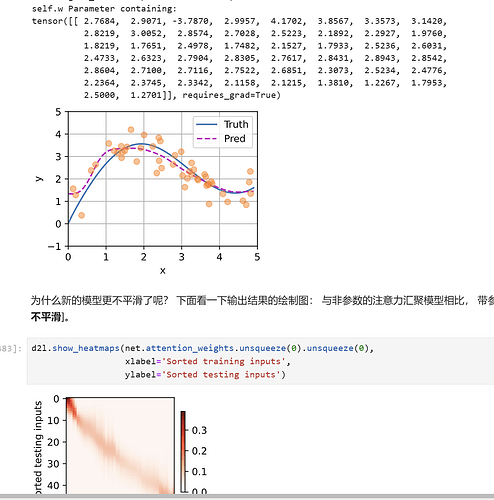
说白了就是把train数据，拆分成49个key和一个query，主对角线也是为了保证每个样本都做一次key，然后训练这种注意力机制下参数的学习。
最优不代表曲线一定符合预期，只是说模型收敛的做好而已
去掉对角，实际就是每组训练数据都缺一个，然后来训练，让其还原出来，等价于，通过其它所有数据来预测缺失的一个，当然，训练时肯定要将每个值都训练一次，这样训练效果比较好，所以是对角。
可以把当前的x用上，但是不平滑。主要由于这里只用了一个w，且只有少数的几个x（看一下高斯核的形状）
要用x附近更多的样本，也就是把$nn.functional.softmax(-(X_repeat - x_train)**2 / 2$，这里除以128，把这个高斯核变的更宽一点。这样就平滑了
用Nadaraya-Watson回归去类比attention机制，并不合适。Nadaraya-Watson回归类似KNN(K-nearest neighbors), 是通过多个邻近的sample去预测一个新的sample。
而attention，是通过捕捉一个sample(e.g. text)里多个feature(e.g. word)之间关系，预测该sample的对应的值(e.g. 该text的英文翻译结果)。这发生在同一个sample里。
有没有可以举例：多元线性回归中，通过多个features(x1, x2, x3, x4, x5, x6, 此处x是不同的feature，不是sample)预测y。怎样把attention机制用于其中呢？
前面有个-1/2的，所以越接近其绝对值越小（值越大），所以softmax后越大。
为什么这里只有一个权重w，而不是一个键对应一个w?
模型定义为:
class NWKernelRegression(nn.Module):
def __init__(self, **kwargs):
super().__init__(**kwargs)
self.w = nn.Parameter(torch.rand((1,), requires_grad=True))
def forward(self, q, k, v):
q = q.repeat_interleave(k.shape[1]).reshape((-1, k.shape[1])) # q:[[q00, q00, q00, ...], [q01, q01, ...], ...]
# print(q)
# q = q.unsqueeze(1)
self.attention_weights = nn.functional.softmax(-((q - k) ** 2) / 2 * self.w, dim=1)
return torch.bmm(self.attention_weights.unsqueeze(1), v.unsqueeze(-1)).reshape(-1)
# return (self.attention_weights * values).reshape(-1)
其中, $$q = q.repeat_interleave(k.shape[1]).reshape((-1, k.shape[1]))$$进行处理了q的维度.
我发现可以广播实现, 即:
(q.unsqueeze(1) - zero) == q.repeat_interleave(k.shape[1]).reshape((-1, k.shape[1]))
结果为True.
但我替换为q = q.unsqueeze(1)时, 前向传播结果不相等.这是为什么?
例子里只有一个参数w，我把它改成了给每个样本(x_i,y_i)一个w_i。因为改了之后，w向量得和query这个矩阵的列数一致，但是训练过程和测试过程的query矩阵的列数是不一样的，所以我就把训练过程的query和key，value矩阵每行删除一个元素这个操作去掉了。
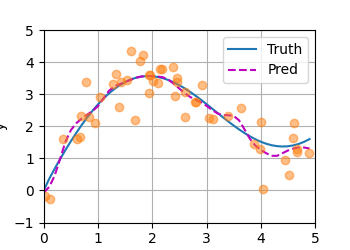
修改之前的：w是一个标量，结果如图：
，可以看到，过拟合了。模型过于复杂，数据过于少导致过拟合。
下图是修改后的，w是一个1*keys的列数的向量：
可以看到，过拟合的现象减轻了，明显更平滑了。
总结的太好了，让我豁然开朗，增加权重的意义在于使得对于远距离的key 有着更小的关注，缩小的注意力的范围。
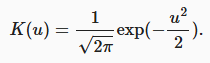
u越小，因为加了负号，所以K越大
去掉对角线元素是为了不让训练数据去减去自身导致其点损失为0而使函数朝着局部最小值的方向优化导致过拟合而忽略了其他的数据呀
l = l.sum() + torch.sqrt(net.w) 加了一下正则之后感觉fit得不错