http://zh.d2l.ai/chapter_attention-mechanisms/nadaraya-waston.html
1 Like
我有两点没太弄懂：
1.在带参数的注意力汇聚中，最终的拟合结果看上去应该是相对于非参数注意力汇聚更好，但是文中更多的强调的是“更不平滑”，这里的“更不平滑”会为模型带来哪些负面影响呢？
2.在非参数注意力汇聚中，介绍了键、查询、值之间的关系，在本例中通过生成了训练集和测试集数据来模拟这种关系，为什么训练数据对应的是“键”，测试数据对应的是“查询”呢？能否将测试数据和训练数据所对应的内容互换呢？
4 Likes
在参数注意力汇聚部分中，最后绘制热力图的时候需要为权重添加detach()才可以：
d2l.show_heatmaps(net.attention_weights.unsqueeze(0).unsqueeze(0).detach(),
xlabel='Sorted training inputs',
ylabel='Sorted testing inputs')
否则会报错：
RuntimeError: Can't call numpy() on Tensor that requires grad. Use tensor.detach().numpy() instead.
-
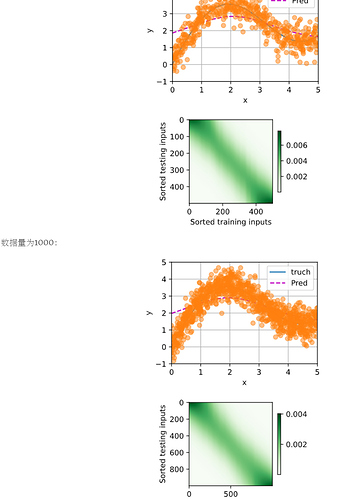
增加数据量无法得到更好的拟合效果：
发现拟合效果并没有很大的变化，说明与数据量无关。其实也好理解，如果仅仅增加数据量的话，变化的仅仅是权重矩阵的规模，而权重矩阵仅仅是由训练数据和测试数据的差值经过一层线性变换得到，其表达能力不够(欠拟合)。 -
那么，学习得到的参数w的价值是什么？
我们将参数w输出来看一下：
tensor([23.3051], requires_grad=True)
值大约为23，且参数w只是一个标量参数，不是向量，那就说明w都是相同的参数23，我们试着将非参数注意力汇聚添加一个23的权重：
attention_weights = nn.functional.softmax(-((x_repeat - x_train) * 23)**2 / 2, dim=1)
可以得到类似参数注意力汇聚一样的效果。
可以发现这样的话拟合效果就更好了，但是也变成了和参数注意力汇聚一样尖锐的加权区域。那么为什么在可视化注意力权重时，它会使加权区域更加尖锐？
我们观察上述公式发现，w加在(x-x_i)外，平方之内，乘以一个-1/2之后就相当于绝对值扩大了230倍左右，我们知道softmax函数在x趋向负无穷的时候值无限趋近于0，所以这样一来就保留了键和查询之间的差距足够小的pair，过滤掉了键和值差距较大的pair，从而达到注意力效果，使得预测结果更加准确。
- 如上述添加一个固定的权重23即可得到更好的拟合效果。
21 Likes
个人理解：
对第一点，“更不平滑”意味着模型训练有“过拟合”倾向，即结果受到加入的噪声影响过大。
对第二点，“查询”是输入，“键”是输入时模型存好的。测试模型时，输入是测试数据，所以训练数据对应“键”，测试数据对应“查询”。
1 Like
针对1问题，当你使用无参数的注意力汇聚的时候，因为没有参数，增加数据量是不会改变注意力函数的。所谓学习就是是通过数据调整参数的过程，所以没有参数，增加数据量拟合效果不变。
2 Likes
对于第一个问题，认同pyao的观点，折线过多意味着在过拟合了。 10.2.3例子中可以把 attention_weights 作为参数进行训练，你会发现最后的结果完全匹配所有的y_train, 但是全部都是折线。
对于第二个问题，键值是一个整体，你可以认为一个黑盒子，是我们训练好的网络，query你是要向这个网络来查询一个输入对应的输出，根据任务，我们要通过x_test来查询y_test值。
2 Likes
10.2.4.2 里面
self.w = nn.Parameter(torch.rand((1,), requires_grad=True))
可以换成
self.w = nn.Parameter(torch.rand((n_train,), requires_grad=True))
效果会更好
4 Likes
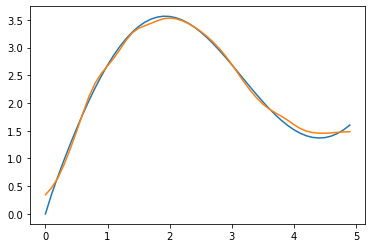
“不如之前非参数模型的平滑。”
可这是一条横线啊，这里出了什么问题？
你理解错了，这里的 非参数模型 指的是 10.2.3. 非参数注意力汇聚中的模型
1 Like
我看的d2l网站上面pytorch版的这个图错了，
这是我的结果图片
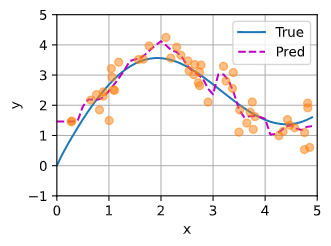
w 就是一个惩罚因子 越偏离的权重越小 偏离程度越接近0的惩罚的作用就自然小了，权重相对就大
1 Like
我第一遍也遇到了这个问题，重启内核，然后重新运行整个notebook就好了。
10.2.4.3 任何一个训练样本的输入都会和除自己以外的所有训练样本的“键－值”对进行计算
为什么训练的时候要去掉自己本身呢
1 Like
是因为不去掉的话过拟合特别快吗？ 
请问这里的Query，Keys，Values分别对应这什么呢？
Query，Keys，Values分别对应查询、键、值
在非参注意力汇聚的部分，选用高斯核，当 x_i 越接近 x 时，分子应该越小，权重不应该越小吗？怎么会越大呢？
w就是一个实数,我想的是结合softmax会使得weight变化更大,本来还想怎么形容这个变化,看到你说惩罚因子我就觉得很贴切.
1 Like