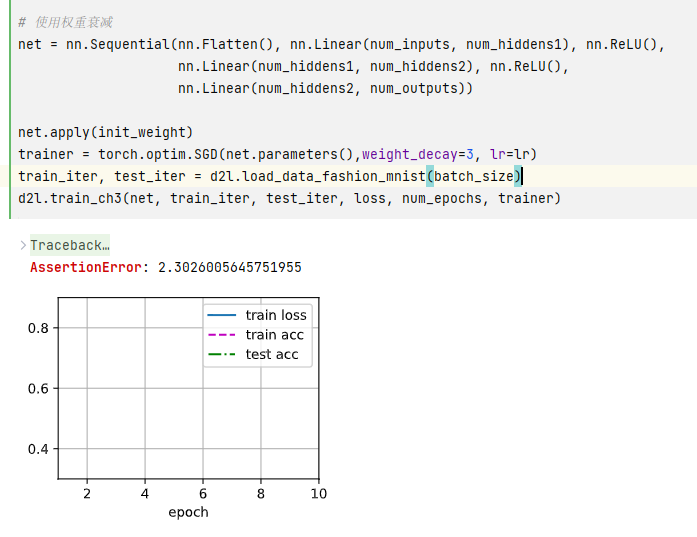
已经成为专业术语。。。倒也不必计较 。。。。。。。。。。。。
练习一
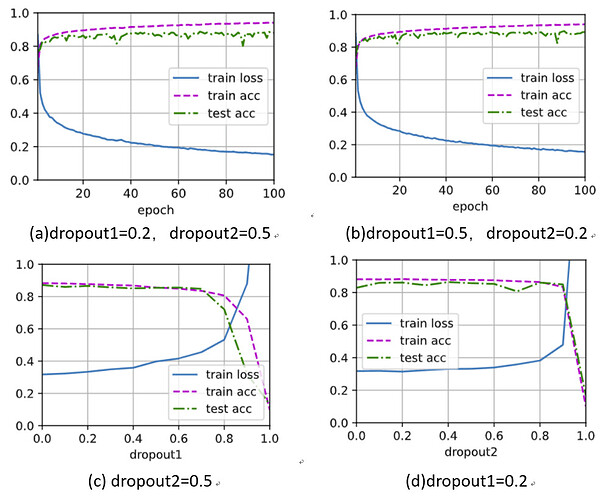
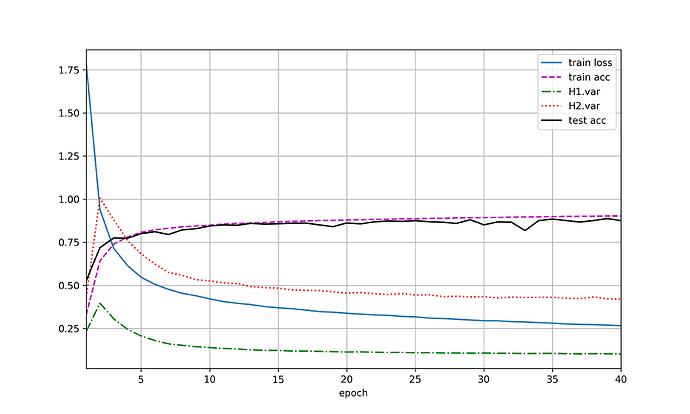
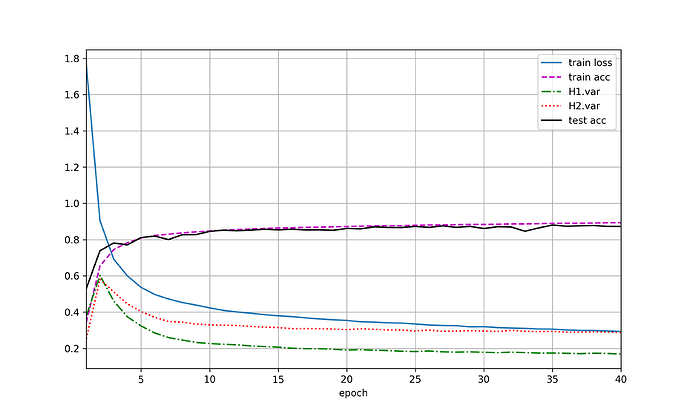
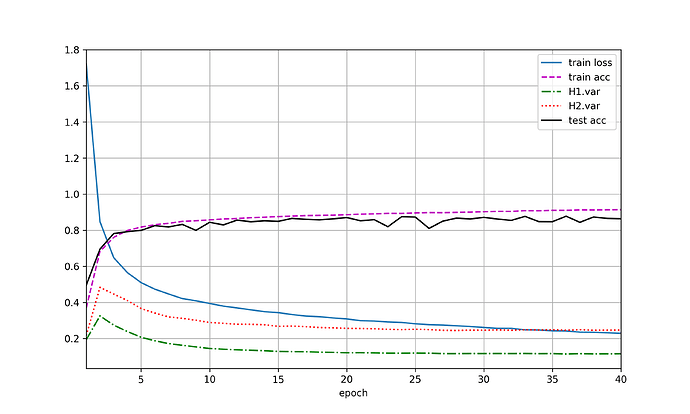
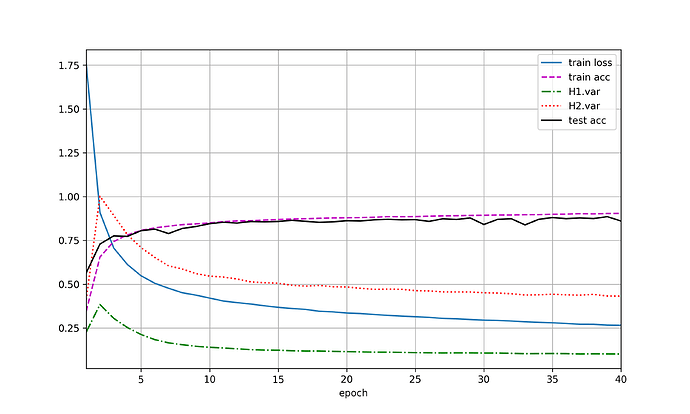
未交换二者暂退概率的图(a),交换二者暂退概率后如(b),两图之间没有较大差异。
为了进一步探究,设置了两组实验,分别是:
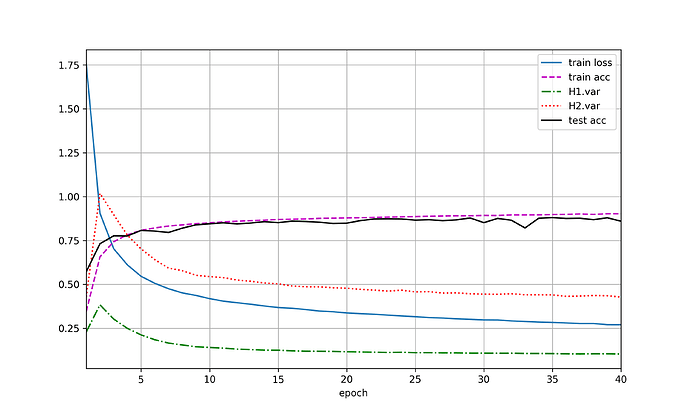
(1)将dropout2固定为0.5,观察dropout1变化对网络训练及测试的影响。如图(c)可以观察到随着rate1的增加,前半阶段(0-0.5)网络性能变化不大,且dropout一定程度上减缓了网络过拟合问题,但后续继续增大rate1,网络的性能有较明显的下降趋势。
(2)将dropout1固定为0.2,观察dropout2变化对网络训练及测试的影响。如图(d)曲线趋势和(c)相似,但网络性能在较后的地方出现了明显下降。
原始的 dropout 论文建议输入层的 p=0.2,而隐藏层的 p=0.5。个人理解这两个实验图也在一定程度上说明了dropout的一些调参经验吧,即靠近输入层的地方应当保留较多信息,而隐含层则可以适当丢弃较多节点。
练习二
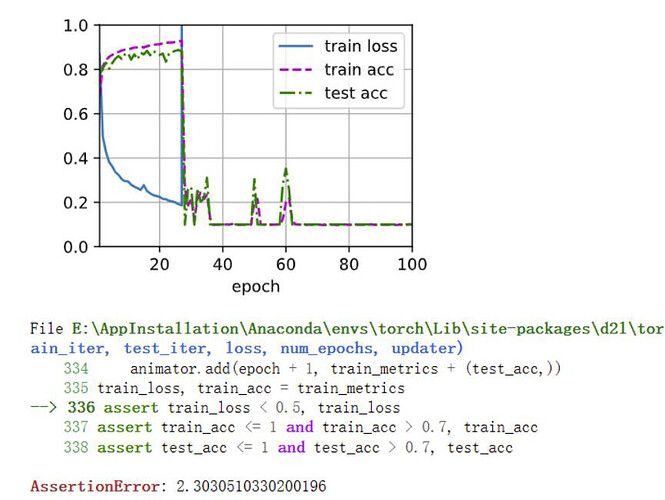
使用暂退法参考练习一图(a),不使用暂退法见下图,网络出现了明显的梯度爆炸。原因推测为反向传播时梯度增长过大,导致网络权重的大幅更新,使网络变得不稳定。至于为什么dropout抑制了网络的梯度爆炸,应该dropout引入了噪声,使网络更平滑有关吧。
另外使用dropout的网络应当会比未使用dropout的网络收敛更慢,但这里模型比较简单,没有很明显的体现。
练习三
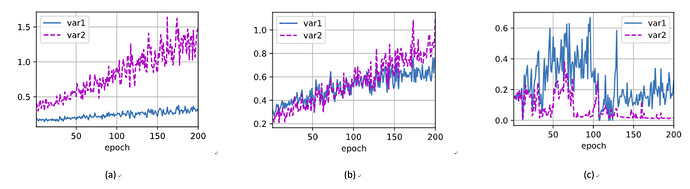
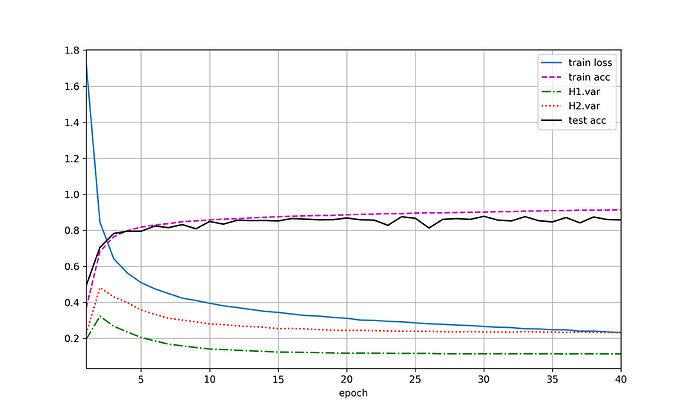
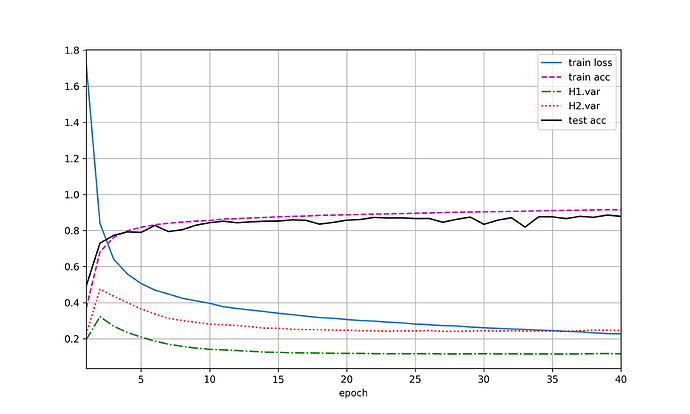
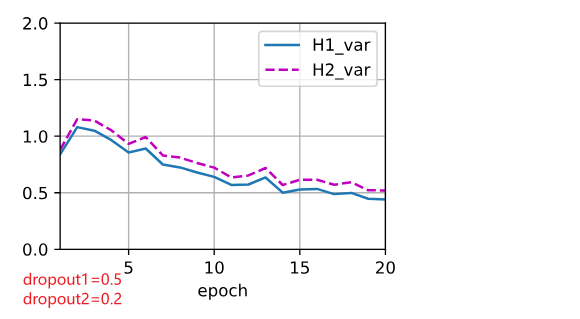
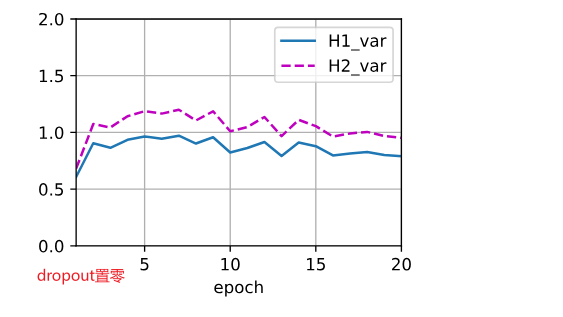
使用暂退法,dropout1, dropout2 = 0.2, 0.5,隐藏层激活值方差随epoch变化如图(a),var1指隐藏层1激活值方差,var2指隐藏层2激活值方差。交换二者比率,结果有(b)。未使用暂退法则有结果(c)。
加入dropout后,方差明显有虽epoch上升的趋势,且dropout的p值越高,方差上升速度越快,但整体上,var1上升速度小于var2。
练习四
因为dropout会引入噪声吧,影响测试效果。
代码中 nn.Linear() 会把 w 进行 kaiming 正态分布初始化 是一种适用于 RELU 激活函数的初始化。
bias 根据输入输出维度自动做调整。
loss函数中loss = nn.CrossEntropyLoss(reduction = ‘none’)把括号里的加上去
代码在哪里体现暂退法只在训练期间有效呢?
练习三,我求方差的方法是修改自定义net类的forward函数,添加
self.H1_var=((H1.mean()-H1)**2).sum()/H1.numel()
self.H2_var=((H2.mean()-H1)**2).sum()/H2.numel()
了这些语句,然后就可以调用net来求每一层的方差了。额为什么我的方差是呈越来越小的趋势的???
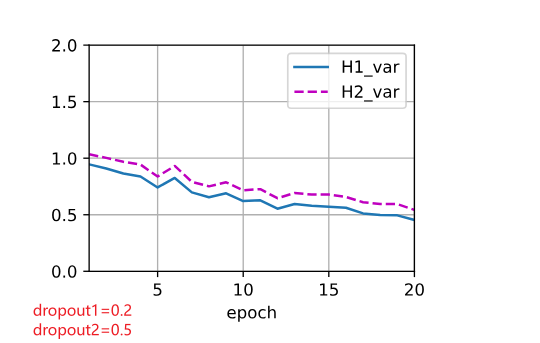
学习率取值为0.01
4.6.4节的dropout_layer函数中,是将输入的X进行dropout,那么对于10010这样的输入数据而言,每一组输入数据(110的向量)所对应的杀死的神经元是不一样的。
而图4-3中是对隐藏层中的神经元节点进行随机杀死,对于100组数据,杀死的都是一些固定的神经元,因此感觉这里有一些代码和示意图的不一致,应该按照哪个进行理解呢。
因为如果要对损失进行梯度下降,那么损失应该为一个标量。删去reduction=‘none’ ,会默认计算损失的均值,即把损失从张量变为了标量,这样才可以用于梯度计算。
在dropout从零开始实现的代码中,为什么没有见到权重初始化工作?可以不用初始化,直接训练模型吗??
100*10这样的输入数据而言,上面打错了
脱敏这个说法我赞同,另外,我把他叫做局部麻木法 ![]()
pytorch具体是怎么实现训练时dropout但是测试时不dropout的?代码如何?该文章似乎没讲
“正则化”已经成为机器学习术语,“简单化”反而会引起歧义了。
When you pass an input to a model instance, PyTorch automatically calls the model’s forward method.
import torch
from torch import nn
from d2l import torch as d2l
def dropout_layer(X, dropout):
assert 0 <= dropout <= 1
if dropout == 1:
return torch.zeros_like(X)
if dropout == 0:
return X
mask = (torch.rand(X.shape) > dropout).float()
return mask * X / (1.0 - dropout)
def noise_layer(X):
Noise = torch.normal(0, 0.01, X.shape) #添加随机噪声
return Noise + X
def init_weights(m):
if type(m) == nn.Linear:
torch.manual_seed(1) #设置随机种子
nn.init.normal_(m.weight, std=0.01)
class Net(nn.Module):
def __init__(self, num_inputs, num_outputs, num_hiddens1, num_hiddens2, is_training = True):
super(Net, self).__init__()
self.num_inputs = num_inputs
self.training = is_training
self.lin1 = nn.Linear(num_inputs, num_hiddens1)
self.lin2 = nn.Linear(num_hiddens1, num_hiddens2)
self.lin3 = nn.Linear(num_hiddens2, num_outputs)
self.relu = nn.ReLU()
def forward(self, X):
H1 = self.relu(self.lin1(X.reshape((-1, self.num_inputs))))
if self.training == True:
H1 = dropout_layer(H1, dropout1)
H2 = self.relu(self.lin2(H1))
if self.training == True:
H2 = dropout_layer(H2, dropout2)
out = self.lin3(H2)
return (out, H1.var(), H2.var())
#暂退法应用到权重矩阵的各个权重
# def forward(self, X):
# H1 = self.lin1(X.reshape((-1, self.num_inputs)))
# if self.training == True:
# H1 = dropout_layer(H1, dropout1)
# H1 = self.relu(H1)
# H2 = self.lin2(H1)
# if self.training == True:
# H2 = dropout_layer(H2, dropout2)
# H2 = self.relu(H2)
# out = self.lin3(H2)
# return (out, H1.var(), H2.var())
# 仅训练时为每一层注入随机噪声,且不同于暂退法。
# def forward(self, X):
# H1 = self.relu(self.lin1(X.reshape((-1, self.num_inputs))))
# if self.training == True:
# H1 = noise_layer(H1)
# H2 = self.relu(self.lin2(H1))
# if self.training == True:
# H2 = noise_layer(H2)
# out = self.lin3(H2)
# return (out, H1.var(), H2.var())
def evaluate_accuracy(net, test_iter):
net.eval()
net.training = False #测试时关闭暂停法
metric = d2l.Accumulator(2)
with torch.no_grad():
for X, y in test_iter:
metric.add(d2l.accuracy(net(X)[0], y), y.numel())
return metric[0] / metric[1]
def train_epoch_ch3(net, train_iter, loss, updater):
net.train()
net.training = True #训练时开启暂停法
metric = d2l.Accumulator(5)
for X, y in train_iter:
updater.zero_grad()
y_hat, H1_var, H2_var = net(X)
l = loss(y_hat, y)
l.backward()
updater.step()
metric.add(float(l.sum() * len(X)), d2l.accuracy(y_hat, y), y.numel(), float(H1_var)*y.numel(), float(H2_var)*y.numel())
return metric[0] / metric[2], metric[1] / metric[2], metric[3] / metric[2], metric[4] / metric[2]
def train_ch3(net, loss, num_epochs, updater):
animator = d2l.Animator(xlabel='epoch', xlim=[1, num_epochs],
legend=['train loss', 'train acc', 'H1.var', 'H2.var', 'test acc'], figsize=[10,6])
for epoch in range(num_epochs):
train_iter, test_iter = d2l.load_data_fashion_mnist(256) #保证每轮训练集顺序不一样,但是测试集一样
train_metrics = train_epoch_ch3(net, train_iter, loss, updater) #训练启用dropout
train_loss, train_acc, _, _ = train_metrics
test_acc = evaluate_accuracy(net, test_iter) #测试关闭dropout
animator.add(epoch + 1, train_metrics + (test_acc,))
train_loss, train_acc, _, _ = train_metrics
assert train_loss < 0.5, train_loss
assert train_acc <= 1 and train_acc > 0.7, train_acc
assert test_acc <= 1 and test_acc > 0.7, test_acc
print(f'train_acc = {train_acc}, test_acc = {test_acc}')
# 使用暂退法每个隐藏层中激活值的方差
num_epochs, lr = 40, 0.1 #训练40轮,学习率为0.1
dropout1, dropout2 = 0.2, 0.5
num_inputs, num_outputs, num_hiddens1, num_hiddens2 = 784, 10, 256, 256
net = Net(num_inputs, num_outputs, num_hiddens1, num_hiddens2)
net.apply(init_weights);
loss = nn.CrossEntropyLoss(reduction='mean')
trainer = torch.optim.SGD(net.parameters(), lr=lr)
train_ch3(net, loss, num_epochs, trainer)
# 使用plt.savefig()并指定参数
d2l.plt.savefig(r'E:\dropout.png', dpi=300)
#其他情况类似
#各种情况最后结果
仅仅使用暂退法:train_acc = 0.9024666666666666, test_acc = 0.8755
交换第一层和第二层:train_acc = 0.8932166666666667, test_acc = 0.8725
暂退法和权重衰减:train_acc = 0.9020166666666667, test_acc = 0.8595
仅仅权重衰减:train_acc =0.91395, test_acc = 0.8579
两者都没有:train_acc = 0.9143, test_acc = 0.8641
暂退法应用到权重矩阵:train_acc = 0.90415, test_acc = 0.8605
随机噪声法:train_acc = 0.9152833333333333, test_acc = 0.8789
哦哦,原来是这么一回事啊,我还以为是那个正则呢 ![]()
请教一下,为什么你算方差的时候是整个batch的隐藏层激活值一起算出来一个方差,而不是每个输入样本对应的隐藏层激活值各算一个方差(即一个batch应该算出来256个方差)?