Jun '20
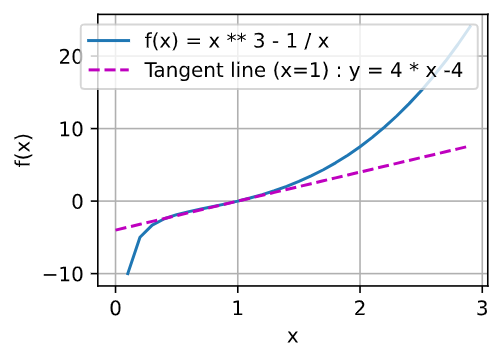
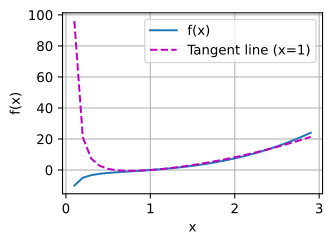
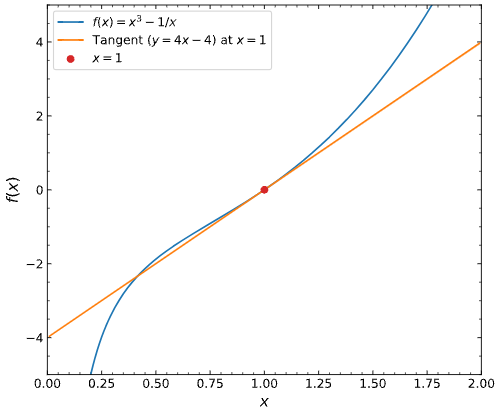
x = np.arange(0, 3, 0.1)
plot(x, [x ** 3 - 1 / x, 4 * x - 4], 'x', 'f(x)', legend=['f(x) = x ** 3 - 1 / x ', 'Tangent line (x=1) : y = 4 * x - 4 '])
According to the power rule and multiple rule," 3 * x ** 2 + 1 / (x ** 2) "is the derivative function of f (x).
So x == 1,f’(1) ==3 * 1 **2 + 1 / (1 ** 2) == 3 + 1 == 4,tangent line’s slope is 4.
And we know, the tangent line passes the plot (1, 0).
So the function of the line is " y == 4 * (x - 1) == 4 * x -4"
I have some problem with saving the “plot” picture, so I just screenshoted it.
I can still remember it is easy to save other “plot” pictures (eg. Statsmodel)by double-clicking the pic and clicking the “save” botton in VScode.
Is there a way to save instead of screenshoting ?
2 replies
Jun '20
Jun '20
Hi,
Thanks for the great content guys gradients and chain rule would be really helpful
2 replies
Jun '20
▶ anandsm7
Jul '20
Aug '20
For the 2nd question in Excercises. Do we have different variables x1 and x2 or is it a single variable x ? If it’s a single variable, is it 5ex^2 that is in the equation?
1 reply
Sep '20
▶ akhil_teja
Sep '20
Hi does D2L provide a way where we can validate or check our solutions for the exercises ?
2 replies
Sep '20
▶ rammy_vadlamudi
Discussion is the only way now.@rammy_vadlmudi
Sep '20
▶ rammy_vadlamudi
Hey @rammy_vadlamudi , yes! This discussion forum is great way to share your thoughts and discuss the solutions. Feel free to voice it out!
Sep '20
Hey guys hope u all good. I’ve found today this course. It’s quite interesting. I’m completing it in python. I’m learning mostly python for machine learning and AI applications. Even i’ve been learning how to manage to use AWS sagemaker and clouds services. But i wanted to ask a question about finding the gradient of the function. I mean question 2: It’s possible to definex[0]**2 + 5 np.exp(x[1])
thanks in advance
2 replies
Oct '20
▶ Luis_Ramirez
Hi @Luis_Ramirez , your logic is never dump! differentiable step and then apply the chain rule (i,e., we define all the derivative formula in code and apply chain rule). Check https://d2l.ai/chapter_preliminaries/autograd.html for more details. Besides, if you would like to see how to code from scratch, check here . Let me know if it helps!
Oct '20
▶ StevenJokes
Try adding this line to the top of the plot function:
fig = d2l.plt.figure()
and have the plot function
return fig
then:
def f(x)
return(x**3-1/x)
x = np.arange(0.1, 3, 0.1)
fig = plot(x, [f(x), 4 * x-4], 'x', 'f(x)', legend=['f(x)', 'Tangent line (x=1)'])
fig.savefig("2_Prelim 4_Calc 1_Ex.jpg")
Apr '21
▶ Luis_Ramirez
hello,
¿it’s ok?
Apr '21
Hi, I’m looking for some clarification on this excerpt from the very end of Section 2.4.3:
Similarly, for any matrix 𝐗, we have ∇𝐗 ‖𝐗‖_F^2 = 2𝐗.
Does this mean that for a given matrix of any size filled with m*n variables, the gradient of the square of that matrix can be condensed to 2X?
Also, what does the subscripted F imply in this case?
Thanks!
1 reply
Apr '21
Hi, I just wanted to verify my solutions for the provided exercise questions:
Find the gradient of the function 𝑓(𝐱)=3*(𝑥1 ^ 2) + 5𝑒^𝑥2
(Subsituting y for x2, as I assumed x1 != x2)
f’(x) = 6x + 5e^y
What is the gradient of the function 𝑓(𝐱)=‖𝐱‖2
||x||2 = [ (3x^2)^2 + (5e^y)^2 ]^0.5
(Calculating the Euclidean distance using the Pythagorean Theorem)
||x|| = ( 9x^4 + 25e^2y ) ^ 0.5
f’ ( ||x|| ) = ( 18x^3 + 25e^2y ) / ( 9x^4 + 25e^2y ) ^ 0.5
Can you write out the chain rule for the case where 𝑢=𝑓(𝑥,𝑦,𝑧), 𝑥=𝑥(𝑎,𝑏), 𝑦=𝑦(𝑎,𝑏), and 𝑧=𝑧(𝑎,𝑏)?
Is this meant to be simplified to df/dx * (dx/da + dx/db) and so on for y, and z?
Thanks so much, and I apologise if my answers are completely misguided.
Aug '21
Find the gradient of the function f (x) = 3x12 + 5e x2
x1/df = 6x + 5 e^x22 e^x2
∇ x f (x) = [6x + 5 ex2, 52 e x2]
here is pic (not sure if it’s correct)
1 reply
Aug '21
▶ VolodymyrGavrysh
I’m confused with partial derivatives. Since for partial derivatives we can treat all other variables as constants, shouldn’t the derivative vector be [6x_1, 5e^x_2] ?
∂f/∂x_1 = ∂/∂x_1 (3x_1^2) + DC = 6x_1 + 0 = 6x_1 (C being a constant)
Aug '21
▶ t1dumsharjah
I believe the F implies the Frobenius Norm:http://d2l.ai/chapter_preliminaries/linear-algebra.html?highlight=norms
I’m not clear on what the notation implies when there is both a subscript F and a superscript 2. The text reads as if the Frobenius Norm is always the square root of the sum of its matrix elements, so the superscript should always be 2. Is this understanding incorrect?
1 reply
Nov '21
Exercise 2:x ) = [6x1, 5e^x2]
Exercise 3:x ) = (x1² + x2² … + xn²)¹/²x ) = x /f(x )
Exercise 4:
du/da = (du/dx)(dx/da) + (du/dy)(dy/da) + (du/dz)(dz/da)
Jan '22
▶ xela21co
The superscript 2 means you are squaring the Forbenius Norm. So, the square root in the Forbenius Norm disappears.
Mar '22
I found some issue, while I run the below code in pytorch.
x = np.arange(0, 3, 0.1)
plot(x, [f(x), 2 * x - 3], 'x', 'f(x)', legend=['f(x)', 'Tangent line (x=1)'])
1 reply
Mar '22
▶ zgpeace
Mar '22
▶ anirudh
Thank you @anirudh . I try to install d2l without version. !pip install d2l It works.
Jun '22
For question one:
def f(x):
return x ** 3 - 1.0 / x
def df(x):
return 3 * x ** 2 + 1/ (x * x)
def tangentLine(x, x0):
"""x is the input list, x0 is the point we compute the tangent line"""
y0 = f(x0)
a = df(x0)
b = y0 - a * x0
return a * x + b
x = np.arange(0.1, 3, 0.1)
plot(x, [f(x), tangentLine(x, 2.1)], 'x', 'f(x)', legend=['f(x)', 'Tangent line (x=2.1)'])
Aug '22
the calculus.ipynb notebook kernel dies each time I run:
x = np.arange(0, 3, 0.1)
plot(x, [f(x), 2 * x - 3], 'x', 'f(x)', legend=['f(x)', 'Tangent line (x=1)'])
What am I supposed to do here? Thanks
Dec '22
Would the idea be to use a ‘generalized’ chain rule and express du/da, and du/da (something like the gradient)
du/da = f’(dx/a) + f’(dy/da) + f’(dz/da)
Dec '22
tx = 3 * x ** 2 + (1 / x ** 2) - 4
1 reply
Dec '22
In section 2.4.3, you define gradient of a multivariate function assigning vector x to a scalar y.
At the end of the section, you give rules for gradients of matrix-vector products (which are matrices, not scalars).
I think it would help to define gradient of a matrix.
Jan '23
▶ anandsm7
I agree with this, felt like these big topics just got skipped over
May '23
1 reply
Jul '23
Jul '23
Thanks for a great course!
Any idea regarding Q10?
I used the given definitions as hinted - denote g=f^(-1), I was able to derive that
\frac{dg}{dx} = \frac{\frac{dg}{df}\frac{df}{dx}}{\frac{df}{dg}}
Is that the expected solution?
Mar '24
I think the answer of Q10 is…
Jun '24
This forum won’t let me upload a pdf – if you’re interested in looking at my solutions, you’ll have to compile the LaTeX below.
\documentclass{article}
\usepackage{amsmath}
\usepackage{amssymb}
\begin{document}
\section*{Problem 1}
For $f(x) = c$ where $c$ is a constant, we have
$$
\lim_{h \to 0} \frac{f(x + h) - f(x)}{h} = \lim_{h \to 0} \frac{c - c}{h} = 0
$$
For $f(x) = x^n$, we have
\begin{equation}
\begin{split}
\frac{df}{dx} &= \lim_{h \to 0} \frac{(x + h)^n - x^n}{h} \\
&= \lim_{h \to 0} \frac{\binom{n}{0}x^nh^0 + \binom{n}{1}x^{n-1}h^1 + \binom{n}{2}x^{n-2}h^2 + \cdots - x^n}{h} \text{ via the binomial expansion} \\
&= \lim_{h \to 0} \binom{n}{1}x^{n-1}h^0 + \binom{n}{2}x^{n-2}h^1 + \cdots \text{ after cancelling $x^n$ and dividing by $h$} \\
&= \boxed{nx^{n-1}} \text{ since all terms with $h$ approach 0} \\
\end{split}
\end{equation}
For $f(x) = e^x$, we have
\begin{equation}
\begin{split}
\frac{df}{dx} &= \lim_{h \to 0} \frac{e^{x + h} - e^x}{h} \\
&= \lim_{h \to 0} \frac{e^xe^h - e^x}{h} \\
&= \lim_{h \to 0} \frac{e^x(e^h - 1)}{h} \\
&= e^x \times \lim_{h \to 0} \frac{e^h - 1}{h} \\
&= e^x \times 1 \text{by L'Hopital's rule} \\
&= \boxed{e^x} \\
\end{split}
\end{equation}
For $f(x) = \log(x)$
\begin{equation}
\begin{split}
\frac{df}{dx} &= \lim_{h \to 0} \frac{\log(x + h) - \log(x)}{h} \\
&= \lim_{h \to 0} \frac{\log\left(\frac{x + h}{x}\right)}{h} \\
&= \lim_{u \to 0} \frac{\log\left(1 + u\right)}{ux} \text{ with } u = \frac{h}{x} \\
&= \frac{1}{x} \lim_{u \to 0} \frac{\log(1 + u)}{u} \\
&= \frac{1}{x} \lim_{u \to 0} \frac{1}{(1 + u)\ln{10}} \text{ by L'Hopital's rule} \\
&= \boxed{\frac{1}{x\ln{10}}} \\
\end{split}
\end{equation}
This proof is a bit circular since it uses the derivative of $\log(x)$ when applying L'Hopital's rule! If you found a better proof, let me know.
\section*{Problem 2}
For the product rule:
\begin{equation}
\begin{split}
&\text{Prove } \frac{d}{dx} \left[ f(x)g(x) \right] = f(x)g'(x) + g(x)f'(x) \\
&= \lim_{h \to 0} \frac{f(x+h)g(x+h) - f(x)g(x)}{h} \text{ using the definition of a derivative} \\
&= \lim_{h \to 0} \frac{f(x+h)g(x+h) - f(x+h)g(x) + f(x+h)g(x) - f(x)g(x)}{h} \\
&= \lim_{h \to 0} \frac{f(x+h)\left[g(x+h)-g(x)\right] + g(x)\left[f(x+h)-f(x)\right]}{h} \\
&= f(x+0)\lim_{h \to 0} \frac{g(x+h)-g(x)}{h} + g(x)\lim_{h \to 0} \frac{f(x+h)-f(x)}{h} \\
&= \boxed{f(x)g'(x) + g(x)f'(x)} \\
\end{split}
\end{equation}
For the sum rule:
\begin{equation}
\begin{split}
&\text{Prove } \frac{d}{dx} \left[ f(x)+g(x) \right] = f'(x) + g'(x) \\
&= \lim_{h \to 0} \frac{[f(x+h)+g(x+h)] - [f(x)+g(x)]}{h} \\
&= \lim_{h \to 0} \frac{f(x+h) - f(x)}{h} + \lim_{h \to 0} \frac{g(x+h) - g(x)}{h} \\
&= \boxed{f'(x) + g'(x)} \\
\end{split}
\end{equation}
For the quotient rule:
\begin{equation}
\begin{split}
&\text{Prove } \frac{d}{dx} \left( \frac{f(x)}{g(x)} \right) = \frac{g(x)f'(x) - f(x)g'(x)}{g^2(x)} \\
&= \lim_{h \to 0} \frac{\frac{f(x+h)}{g(x+h)} - \frac{f(x)}{g(x)}}{h} \\
&= \lim_{h \to 0} \frac{f(x+h)g(x) - f(x)g(x+h)}{hg(x)g(x+h)} \\
&= \lim_{h \to 0} \frac{f(x+h)g(x)-f(x)g(x)+f(x)g(x)-f(x)g(x+h)}{hg(x+h)g(x)} \\
&= \lim_{h \to 0} \frac{g(x)[f(x+h)-f(x)] - f(x)[g(x+h)-g(x)]}{hg(x)g(x+h)} \\
&= \boxed{\frac{f'(x)g(x) - f(x)g'(x)}{g(x)^2}} \\
\end{split}
\end{equation}
\section*{Problem 3}
The product rule states $\frac{d}{dx}[f(x)g(x)] = f(x)g'(x) + g(x)f'(x)$. Let $g(x) = c$.
$$
f(x)\frac{d}{dx}c + c\frac{d}{dx}f(x) = f(x)\cdot0 + c\frac{d}{dx}f(x) = \boxed{c\frac{d}{dx}f(x)}
$$
\section*{Problem 4}
\begin{equation}
\begin{split}
y &= x^x \\
\ln{y} &= \ln{x^x} = x\ln{x} \\
\frac{1}{y}\cdot\frac{dy}{dx} &= \ln{x} + x \cdot \frac{1}{x} \text{ by the product rule} \\
\frac{dy}{dx} &= y(\ln{x} + 1) \\
\frac{dy}{dx} &= x^x(\ln{x} + 1) \\
\end{split}
\end{equation}
\section*{Problem 5}
$f(x)$ has a slope of 0 at that point. For instance, $f(x) = x^2$ has a slope of 0 at $x = 0$.
\section*{Problem 6}
Done using $3x^2 + \frac{1}{x^2}$ to calculate the slope, yielding the final equation $4x-4$.
\section*{Problem 7}
$$
\nabla_x f(x) =
\begin{bmatrix}
6x_1 \\
5e^{x_2} \\
\end{bmatrix}
$$
\section*{Problem 8}
\begin{equation}
\begin{split}
f(\mathbf{x}) &= \|\mathbf{x}\|_2 \\
\nabla_{\mathbf{x}} \|\mathbf{x}\|_2 &= \nabla_{\mathbf{x}} (\mathbf{x}^{\top}\mathbf{x})^{1/2} \\
&= 2\mathbf{x} \cdot \frac{1}{2}(\mathbf{x}^{\top}\mathbf{x})^{-1/2} \\
&= \boxed{\frac{\mathbf{x}}{\|\mathbf{x}\|_2}} \\
\end{split}
\end{equation}
At $x=0$, the gradient is undefined.
\section*{Problem 9}
$$
\frac{\partial{u}}{\partial{a}} = \frac{\partial{u}}{\partial{x}} \cdot \frac{\partial{x}}{\partial{a}} + \frac{\partial{u}}{\partial{y}} \cdot \frac{\partial{y}}{\partial{a}} + \frac{\partial{u}}{\partial{z}} \cdot \frac{\partial{z}}{\partial{a}}
$$
\section*{Problem 10}
\begin{equation}
\begin{split}
y &= f^{-1}(x) \\
x &= f(y) \\
1 &= f'(y) \cdot \frac{dy}{dx} \\
\frac{dy}{dx} &= \frac{1}{f'(y)} \\
\frac{d}{dx}f^{-1}(x) &= \frac{1}{f'(f^{-1}(x))} \\
\end{split}
\end{equation}
\end{document}
2 replies
Jun '24
import numpy
import matplotlib.pyplot as plt
# Code omitted to make the graph look nice: `plt.rcParams.update...`
def f(x):
return x ** 3 - 1 / x
def df(x):
return 3 * x ** 2 + 1 / x ** 2
def tangent(x, x_0):
return df(x_0) * (x - x_0) + f(x_0)
x_0 = 1
x = np.arange(0.01, 2, 0.01)
_, ax = plt.subplots()
ax.plot(x, f(x), label="$f(x) = x^3 - 1/x$")
ax.plot(x, tangent(x, x_0), label="Tangent $(y = 4x - 4)$ at $x=1$")
ax.scatter(x_0, tangent(x_0, x_0), zorder=10, color="tab:red", label="$x=1$")
ax.set(xlabel="$x$", ylabel="$f(x)$", xlim=(0, 2), ylim=(-5, 5))
ax.legend();
Source: Inverse function theorem .
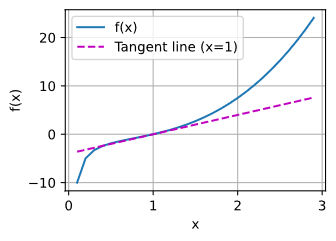
Jul '24
▶ Maxim
your tangent is a line, but your graph shows a curve. Tangent Line is defined as mx+c where m is the slope and c is a constant.
12 Jan
▶ filipv
Revisiting this chapter, I remember being confused by the orientation of the gradients listed in section 2.4.3 – as a hint for other readers, I recommend reading the Layout conventions section of the Matrix calculus Wikipedia Article . This textbook’s appendix, specifically section 22.4.7 is also a great resource.
To summarize, there are two popular conventions for vector-vector derivatives:
In the numerator-based layout (sometimes called the Jacobian layout), the derivative has the same number of rows as the numerator’s dimensionality.
In denominator-based layouts (sometimes called the Hessian or gradient layout), the derivative has the same number of rows as the denominator’s dimensionality. This is sometimes notated by using a gradient symbol, as the authors do here. You also sometimes see a transpose symbol in the denominator to hint the reader that the denominator-based layout is being used.
17 Jan
This seems to be an error.
opened 02:50PM - 17 Jan 25 UTC
In section [2.4.3 2.4.3. Partial Derivatives and Gradients](https://d2l.ai/chapt… er_preliminaries/calculus.html#partial-derivatives-and-gradients), the equation seems to be wrong,
<img width="477" alt="Image" src="https://github.com/user-attachments/assets/5fb2a401-164c-4ec2-b657-a368380103d6" />
It should be
<img width="495" alt="Image" src="https://github.com/user-attachments/assets/bd35af03-e7c1-48c4-9fd9-33c2eddd2e3e" />
If so, I would like to create a pr to fix.
Thanks
13 Feb
In 2.4.10, is $$\mathbf A$$ the Jacobian?
2 Aug
▶ filipv
Your proof for e^x is using circular logic. You are proving the derivative of e^x by using the derivative of e^x in the step that you use l’hopitals.





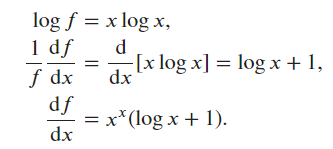


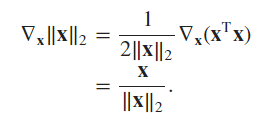
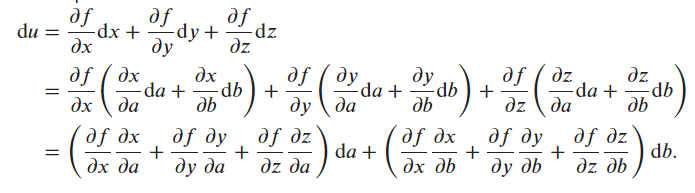
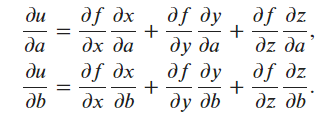




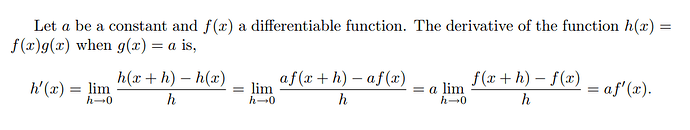
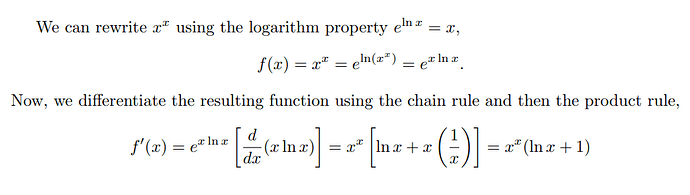
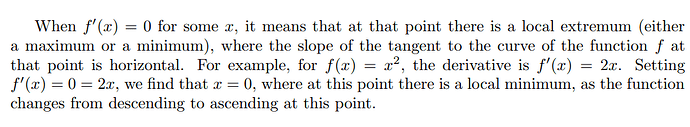

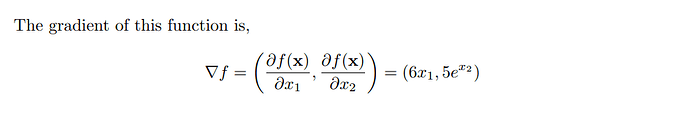

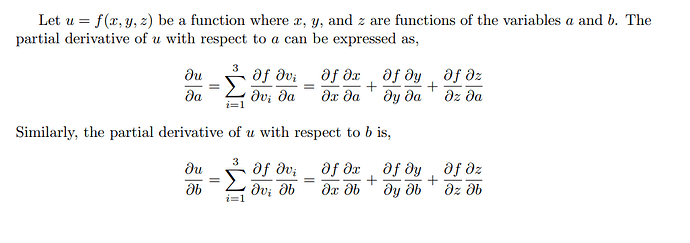
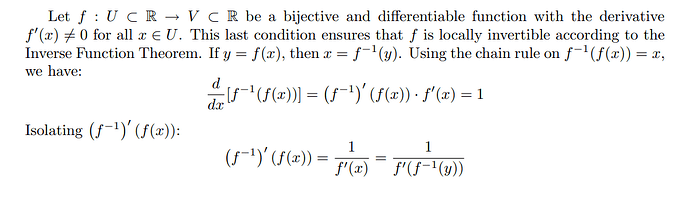
 .
.