Hi,
Thanks for the great content guys 
but i feel like giving examples in gradients and chain rule would be really helpful
Thanks
1 Like
Hi @anandsm7, the gradients and chain rule are in section http://d2l.ai/chapter_appendix-mathematics-for-deep-learning/multivariable-calculus.html#multivariate-chain-rule. Feel free to do a search in the top right of our wensite as here:
2 Likes
some apis:
- plt.gca
Get the current Axes instance on the current figure matching the given keyword args, or create one.
Examples:
To get the current polar axes on the current figure:
plt.gca(projection='polar')
If the current axes doesn’t exist, or isn’t a polar one, the appropriate axes will be created and then returned.
https://matplotlib.org/3.1.1/api/_as_gen/matplotlib.pyplot.gca.html
- axes.cla()
‘’’
Clear an axes, i.e. the currently active axes in the current figure. It leaves the other axes untouched.
‘’’
https://matplotlib.org/api/pyplot_api.html#matplotlib.pyplot.cla.
- fmts:
- ‘-’:solid line style 实线;
- ‘m–’:magenta dashed line style 紫红色虚线;
- ‘g-’:green dash-dotted line style 绿色点划线；
- 'r:'red dotted line style 红色点线
For more:
1 Like
For the 2nd question in Excercises. Do we have different variables x1 and x2 or is it a single variable x ? If it’s a single variable, is it 5ex^2 that is in the equation?
Hi does D2L provide a way where we can validate or check our solutions for the exercises ?
Discussion is the only way now.
@rammy_vadlmudi
Hey @rammy_vadlamudi, yes! This discussion forum is great way to share your thoughts and discuss the solutions. Feel free to voice it out! 
Hey guys hope u all good. I’ve found today this course. It’s quite interesting. I’m completing it in python. I’m learning mostly python for machine learning and AI applications. Even i’ve been learning how to manage to use AWS sagemaker and clouds services. But i wanted to ask a question about finding the gradient of the function. I mean question 2: It’s possible to define
a function like
import numpy as np
def(x): where x is a list
return 3x[0]**2 + 5np.exp(x[1])
and then apply numerical_limit function with following parameters(f = f(x), x =[1,1], h =0.01)
and return a list looping thought each index of the list x =[1,1]
or this logic is too dump?
If you guys can help me
I studied math in the past, but don’t know how to code with the most fresh and efficient way x)
thanks in advance
Hi @Luis_Ramirez, your logic is never dump! In most of DL framework, we decompose a complex function to each directly differentiable step and then apply the chain rule (i,e., we define all the derivative formula in code and apply chain rule). Check https://d2l.ai/chapter_preliminaries/autograd.html for more details. Besides, if you would like to see how to code from scratch, check here. Let me know if it helps!
Try adding this line to the top of the plot function:
fig = d2l.plt.figure()
and have the plot function
return fig
then:
def f(x)
return(x**3-1/x)
x = np.arange(0.1, 3, 0.1)
fig = plot(x, [f(x), 4 * x-4], 'x', 'f(x)', legend=['f(x)', 'Tangent line (x=1)'])
fig.savefig("2_Prelim 4_Calc 1_Ex.jpg")
1 Like
- Q1
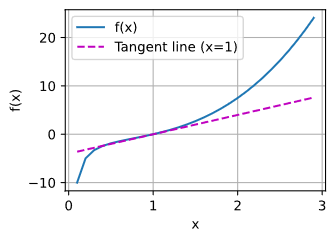
hello,
I tried my code:
import torch
x = torch.arange(2.0)
x.requires_grad_(True)
x.grad
y = 3 * torch.dot(x,x) + 5 * torch.exp(x)
y
y.backward()
x.grad
¿it’s ok?
Hi, I’m looking for some clarification on this excerpt from the very end of Section 2.4.3:
Similarly, for any matrix 𝐗, we have ∇𝐗 ‖𝐗‖_F^2 = 2𝐗.
Does this mean that for a given matrix of any size filled with m*n variables, the gradient of the square of that matrix can be condensed to 2X?
Also, what does the subscripted F imply in this case?
Thanks!
Hi, I just wanted to verify my solutions for the provided exercise questions:
- Find the gradient of the function 𝑓(𝐱)=3*(𝑥1 ^ 2) + 5𝑒^𝑥2
(Subsituting y for x2, as I assumed x1 != x2)
f’(x) = 6x + 5e^y
- What is the gradient of the function 𝑓(𝐱)=‖𝐱‖2
||x||2 = [ (3x^2)^2 + (5e^y)^2 ]^0.5
(Calculating the Euclidean distance using the Pythagorean Theorem)
||x|| = ( 9x^4 + 25e^2y ) ^ 0.5
f’ ( ||x|| ) = ( 18x^3 + 25e^2y ) / ( 9x^4 + 25e^2y ) ^ 0.5
- Can you write out the chain rule for the case where 𝑢=𝑓(𝑥,𝑦,𝑧), 𝑥=𝑥(𝑎,𝑏), 𝑦=𝑦(𝑎,𝑏), and 𝑧=𝑧(𝑎,𝑏)?
Is this meant to be simplified to df/dx * (dx/da + dx/db) and so on for y, and z?
Thanks so much, and I apologise if my answers are completely misguided.
- Find the gradient of the function f (x) = 3x12 + 5ex2
x1/df = 6x + 5e^x2
x2/df = 52e^x2
∇ x f (x) = [6x + 5ex2, 52ex2]
here is pic (not sure if it’s correct)
I’m confused with partial derivatives. Since for partial derivatives we can treat all other variables as constants, shouldn’t the derivative vector be [6x_1, 5e^x_2] ?
∂f/∂x_1 = ∂/∂x_1 (3x_1^2) + DC = 6x_1 + 0 = 6x_1 (C being a constant)
∂f/∂x_2 = DC + ∂/∂x_2 (5e^x_2) = 0 + 5e^x_2 = 5e^x_2
1 Like
I believe the F implies the Frobenius Norm:
http://d2l.ai/chapter_preliminaries/linear-algebra.html?highlight=norms
I’m not clear on what the notation implies when there is both a subscript F and a superscript 2. The text reads as if the Frobenius Norm is always the square root of the sum of its matrix elements, so the superscript should always be 2. Is this understanding incorrect?
Exercise 2:
∇f(x) = [6x1, 5e^x2]
Exercise 3:
f(x) = (x1² + x2² … + xn²)¹/²
∇f(x) = x/f(x)
Exercise 4:
u = f(x,y,z), x = x(a,b), y = y(a,b), z = z(a,b)
du/da = (du/dx)(dx/da) + (du/dy)(dy/da) + (du/dz)(dz/da)
du/db = (du/dx)(dx/db) + (du/dy)(dy/db) + (du/dz)(dz/db)
2 Likes
The superscript 2 means you are squaring the Forbenius Norm. So, the square root in the Forbenius Norm disappears.