Calculus

[ufs]

• Q1
  

[Amalia]

hello,
I tried my code:
import torch
x = torch.arange(2.0)
x.requires_grad_(True)
x.grad
y = 3 * torch.dot(x,x) + 5 * torch.exp(x)
y
y.backward()
x.grad

¿it’s ok?

[t1dumsharjah]

Hi, I’m looking for some clarification on this excerpt from the very end of Section 2.4.3:

Similarly, for any matrix 𝐗, we have ∇𝐗 ‖𝐗‖_F^2 = 2𝐗.

Does this mean that for a given matrix of any size filled with m*n variables, the gradient of the square of that matrix can be condensed to 2X?

Also, what does the subscripted F imply in this case?

Thanks!

[t1dumsharjah]

Hi, I just wanted to verify my solutions for the provided exercise questions:

1. Find the gradient of the function 𝑓(𝐱)=3*(𝑥1 ^ 2) + 5𝑒^𝑥2

(Subsituting y for x2, as I assumed x1 != x2)

f’(x) = 6x + 5e^y

2. What is the gradient of the function 𝑓(𝐱)=‖𝐱‖2

||x||2 = [ (3x^2)^2 + (5e^y)^2 ]^0.5

(Calculating the Euclidean distance using the Pythagorean Theorem)

||x|| = ( 9x^4 + 25e^2y ) ^ 0.5

f’ ( ||x|| ) = ( 18x^3 + 25e^2y ) / ( 9x^4 + 25e^2y ) ^ 0.5

4. Can you write out the chain rule for the case where 𝑢=𝑓(𝑥,𝑦,𝑧), 𝑥=𝑥(𝑎,𝑏), 𝑦=𝑦(𝑎,𝑏), and 𝑧=𝑧(𝑎,𝑏)?

Is this meant to be simplified to df/dx * (dx/da + dx/db) and so on for y, and z?

Thanks so much, and I apologise if my answers are completely misguided.

[VolodymyrGavrysh]

2. Find the gradient of the function f (x) = 3x12 + 5ex2

x1/df = 6x + 5e^x2
x2/df = 52e^x2

∇ x f (x) = [6x + 5ex2, 52ex2]

here is pic (not sure if it’s correct)

[xela21co]

I’m confused with partial derivatives. Since for partial derivatives we can treat all other variables as constants, shouldn’t the derivative vector be [6x_1, 5e^x_2] ?

∂f/∂x_1 = ∂/∂x_1 (3x_1^2) + DC = 6x_1 + 0 = 6x_1 (C being a constant)
∂f/∂x_2 = DC + ∂/∂x_2 (5e^x_2) = 0 + 5e^x_2 = 5e^x_2

[xela21co]

I believe the F implies the Frobenius Norm:
http://d2l.ai/chapter_preliminaries/linear-algebra.html?highlight=norms

I’m not clear on what the notation implies when there is both a subscript F and a superscript 2. The text reads as if the Frobenius Norm is always the square root of the sum of its matrix elements, so the superscript should always be 2. Is this understanding incorrect?

[pbouzon]

Exercise 2:
∇f(x) = [6x1, 5e^x2]

Exercise 3:
f(x) = (x1² + x2² … + xn²)¹/²
∇f(x) = x/f(x)

Exercise 4:
u = f(x,y,z), x = x(a,b), y = y(a,b), z = z(a,b)

du/da = (du/dx)(dx/da) + (du/dy)(dy/da) + (du/dz)(dz/da)
du/db = (du/dx)(dx/db) + (du/dy)(dy/db) + (du/dz)(dz/db)

[imflash217]

The superscript 2 means you are squaring the Forbenius Norm. So, the square root in the Forbenius Norm disappears.

[zgpeace]

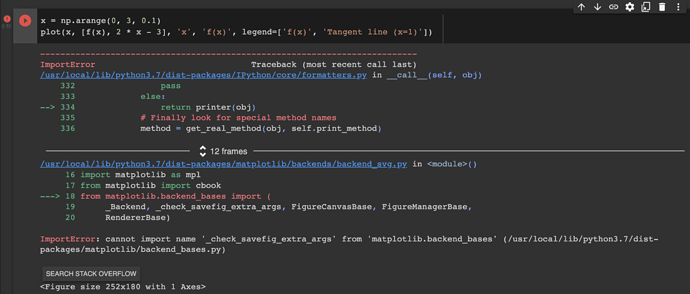
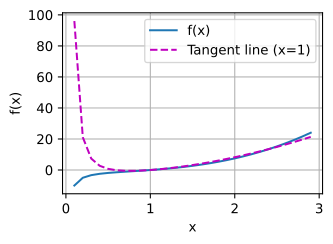
I found some issue, while I run the below code in pytorch.

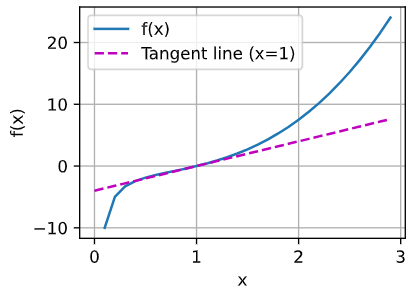
    x = np.arange(0, 3, 0.1)
    plot(x, [f(x), 2 * x - 3], 'x', 'f(x)', legend=['f(x)', 'Tangent line (x=1)'])

[anirudh]

Thanks @zgpeace for raising this, I believe it was recently deprecated but shouldn’t error out. You can try with an older version of ipython. In any case we’ll fix this in the next release https://github.com/d2l-ai/d2l-en/pull/2065

[zgpeace]

Thank you @anirudh. I try to install d2l without version. !pip install d2l It works.

[MrBean]

For question one:

def f(x):
    return x ** 3 - 1.0 / x

def df(x):
    return 3 * x ** 2 + 1/ (x * x)

def tangentLine(x, x0):
    """x is the input list, x0 is the point we compute the tangent line"""
    y0 = f(x0)
    a = df(x0)
    b = y0 - a * x0
    return a * x + b

x = np.arange(0.1, 3, 0.1)
plot(x, [f(x), tangentLine(x, 2.1)], 'x', 'f(x)', legend=['f(x)', 'Tangent line (x=2.1)'])

[bit-scientist]

the calculus.ipynb notebook kernel dies each time I run:

x = np.arange(0, 3, 0.1)
plot(x, [f(x), 2 * x - 3], 'x', 'f(x)', legend=['f(x)', 'Tangent line (x=1)'])

What am I supposed to do here? Thanks

[donny_nyc]

9. Would the idea be to use a ‘generalized’ chain rule and express du/da, and du/da (something like the gradient)

du/da = f’(dx/a) + f’(dy/da) + f’(dz/da)
du/db = f’(dx/db) + f’(dy/db) + f’(dz/db)

[Maxim]

tx = 3 * x ** 2 + (1 / x ** 2) - 4
plot(x, [f(x), tx], ‘x’, ‘f(x)’, legend=[‘f(x)’, ‘Tangent line (x=1)’])

[Denis_Kazakov]

In section 2.4.3, you define gradient of a multivariate function assigning vector x to a scalar y.

At the end of the section, you give rules for gradients of matrix-vector products (which are matrices, not scalars).

I think it would help to define gradient of a matrix.

[cajmorgan]

I agree with this, felt like these big topics just got skipped over

[aniketvp24]

if x is a n dimensional column vector, so x is n by 1, so its transpose is 1 by n and dimension of A is m by n how is x_transpose.A possible then?

[cclj]

Ex4.

• The function is not in the form of any rules given up to now.
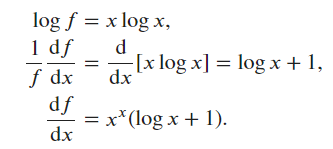
  • Taking the logarithm on both sides yields
    

Ex5.

• Any point 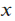such that 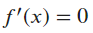indicates a stationary point of a function, where a “ball” standing on the point will hold its position and will not fall along the curve.
  • The stationary point is necessary for a point to be a minimum or maximum point. Sometimes it indicates the critical behavior of a function.
• Example: 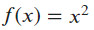at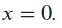

Ex6.

• The derivative
  
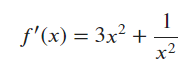
  takes value 4 at point 1.
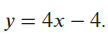
  • The tangent line at point 1 is thus

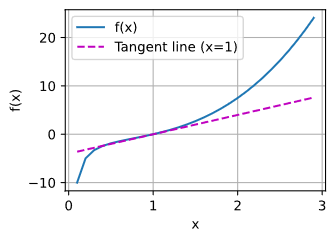
f = lambda x: x ** 3 - 1 / x
x = np.arange(0, 3, 0.1)
plot(x, [f(x), 4 * x - 4], 'x', 'f(x)', legend=['f(x)', 'Tangent line (x=1)'])

Output: