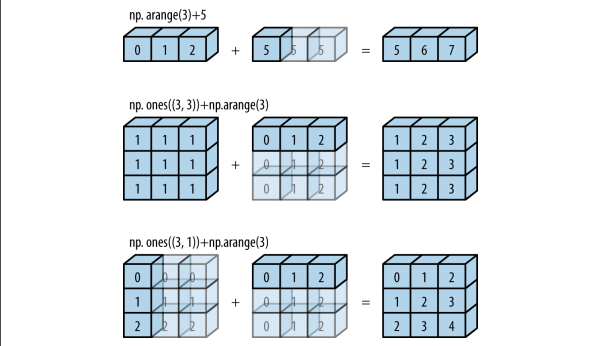
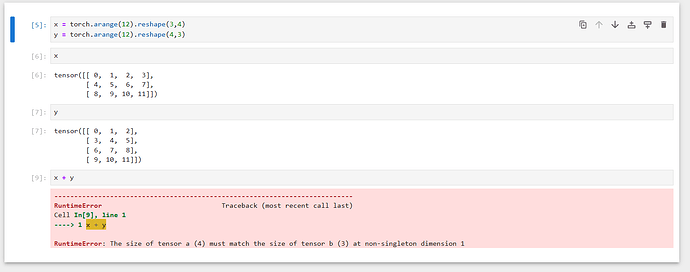
StevenJokes

1.

x = torch.arange(12, dtype=torch.float32).reshape((3,4))
y = torch.tensor([[2.0, 1, 4, 3], [1, 2, 3, 4], [4, 3, 2, 1]])
x,y,x == y,x < y,x > y

(tensor([[ 0., 1., 2., 3.],
[ 4., 5., 6., 7.],
[ 8., 9., 10., 11.]]),
tensor([[2., 1., 4., 3.],
[1., 2., 3., 4.],
[4., 3., 2., 1.]]),
tensor([[False, True, False, True],
[False, False, False, False],
[False, False, False, False]]),
tensor([[ True, False, True, False],
[False, False, False, False],
[False, False, False, False]]),
tensor([[False, False, False, False],
[ True, True, True, True],
[ True, True, True, True]]))

---

2.

a = torch.arange(1, 6, dtype =torch.float32).reshape((5, 1))
b = torch.arange(1, 3).reshape((1, 2))
a, b

(tensor([[1],
[2],
[3],
[4],
[5]]),
tensor([[1, 2]]))

---

a + b

tensor([[2., 3.],
[3., 4.],
[4., 5.],
[5., 6.],
[6., 7.]])

---

a - b

tensor([[ 0., -1.],
[ 1., 0.],
[ 2., 1.],
[ 3., 2.],
[ 4., 3.]])

---

a * b

tensor([[1.0000, 0.5000],
[2.0000, 1.0000],
[3.0000, 1.5000],
[4.0000, 2.0000],
[5.0000, 2.5000]])

---

a / b

tensor([[1, 0],
[2, 1],
[3, 1],
[4, 2],
[5, 2]])

---

a // b

tensor([[1., 0.],
[2., 1.],
[3., 1.],
[4., 2.],
[5., 2.]])

---

a \ b

File “” , line 1 a \ b ^ SyntaxError : unexpected character after line continuation character

---

a ** b

tensor([[ 1., 1.],
[ 2., 4.],
[ 3., 9.],
[ 4., 16.],
[ 5., 25.]])

2 replies

anirudh

@StevenJokes There is no \ operator in pytorch. It is actually a special chracter in python, also called the “escape” character. Hence the error.

Let me know if this is not clear.

1 reply

StevenJokes

I have got it from the doc, but thanks anyway.
I’m a new bee of pytorch.

1 reply

StevenJokes

a % b
tensor([[0., 1.],
[0., 0.],
[0., 1.],
[0., 0.],
[0., 1.]])

manuel-arno-korfmann

When having PyTorch selected:

2.1.5. Saving Memory §3:

Fortunately, performing in-place operations in MXNet is easy.

Is it intentional to discuss MXNet even though PyTorch is selected for the code examples?

1 reply

StevenJokes

It is understandable.
The original examples are built by MXNet. ( created by mli)

hehao98

Allow me to point out a small error in Section 2.1.2
“For stylistic convenience, we can write x.sum() as np.sum(x) .” should not appear in PyTorch version because it is not possible to run np.sum(x) if x is a PyTorch tensor.

x = torch.arange(12)
np.sum(x)
---------------------------------------------------------------------------
TypeError                                 Traceback (most recent call last)
<ipython-input-30-1393831a87e1> in <module>
      1 x = torch.arange(12)
----> 2 np.sum(x)

1 reply

anirudh

Thanks @hehao98 for pointng that out. We have already fixed that line in this commit and it will be updated with our next release.

jairo.venegas

98/5000
Is it only possible to use broadcast when the two arrays have a dimension has value equal to one?

1 reply

goldpiggy

Hi @jairo.venegas, no need to be one. You can broadcast anything This example may give you more idea!

omarkhaled850

in 2.1.4. Indexing and Slicing

X[0:2, :]
this code suppose to take the 1th and 2nd rows, but why it isn’t typed like that -> X[0:1,:]

1 reply

goldpiggy

Hi @omarkhaled850, i am not fully understand your question. Could you elaborate more on that?

1 reply

omarkhaled850

thanks for responding
in the slicing code. we want to take the 1th row (index = 0) and the 2nd row (index = 1) in the example. put the code start from index 0 to index 2 (0:2).
shouldn’t it be (0:1)

1 reply

anirudh

Slicing is an indexing syntax that extracts a portion from the tensor. X[m:n] returns the portion of X :

• Starting with position m
• Up to but not including n

omarkhaled850

thanks man, "Up to but not including n" is the key that i was looking for

Aaron

Hello guys,
In section 2.1.6 [Conversion to Other Python Objects], what do you mean by the line in bold; Unfortunately I can’t get it and I need help. Thanks

Converting to a NumPy tensor, or vice versa, is easy. The converted result does not share memory. This minor inconvenience is actually quite important: when you perform operations on the CPU or on GPUs, you do not want to halt computation, waiting to see whether the NumPy package of Python might want to be doing something else with the same chunk of memory.

Does it mean NumPy and PyTorch are completely independent and may have conflicts with each other?

Edit: According to PyTorch documentation:

Converting a torch Tensor to a NumPy array and vice versa is a breeze. The torch Tensor and NumPy array will share their underlying memory locations, and changing one will change the other.

It says this conversion shares the memory but you said not! Am I right?

1 reply

gphilip

This is probably carried over from the MXNET version, where the corresponding operation does create a copy:

asnumpy () : Returns a numpy.ndarray object with value copied from this array.

@anirudh should be able to confirm/deny this.

1 reply

anirudh

Thanks, @Aaron and @gphilip for raising this. Most part of the book has common text and we are trying to fix issues like these where the frameworks differ in design. Feel free to raise any other issues if you find something similar in other sections on the forum or the Github repo. Really appreciate it!

This will be fixed in the next release.

songjl

e = torch.arange(12).reshape(2, -1, 6)
f = torch.tensor([1, 2, 3, 4]).reshape(-1, 4, 1)
e, f, e.shape, f.shape
(tensor([[[ 0, 1, 2, 3, 4, 5]],

    [[ 6,  7,  8,  9, 10, 11]]]), tensor([[[1],
     [2],
     [3],
     [4]]]), torch.Size([2, 1, 6]), torch.Size([1, 4, 1]))

e + f
tensor([[[ 1, 2, 3, 4, 5, 6],
[ 2, 3, 4, 5, 6, 7],
[ 3, 4, 5, 6, 7, 8],
[ 4, 5, 6, 7, 8, 9]],

    [[ 7,  8,  9, 10, 11, 12],
     [ 8,  9, 10, 11, 12, 13],
     [ 9, 10, 11, 12, 13, 14],
     [10, 11, 12, 13, 14, 15]]])

hojaelee

Hello! I had two questions from this section:

1. Where does the term “lifted” come from? I understand “lifted” means some function that operate on real numbers (scalars) can be “lifted” to a higher dimensional or vector operations. I was just curious if this is a commonly used term in mathematics.

2. Is there a rule for knowing what the shape of a broadcasted operation may be? For Exercise #2, I tried a shape of (3, 1, 1) + (1, 2, 1) to get (3, 2, 1). I also tried (3, 1, 1, 1) + (1, 2, 1) and got (3, 1, 2, 1). It kind of gets harder to visualize how broadcasting will work beyond 3-D, so I was wondering if someone could explain why the 2nd broad operation has the shape that it has intuitively.

Thank you very much!

2 replies

ddptr

Lifting is commonly used for this operation in functional programming (e.g. in Haskell), probably it has some roots in lambda calculus.

imflash217

@hojaelee , During broadcasting the shape matching of the two inputs X, Y happen in reverse order i.e. starting from the -1 axis. This (i.e. -ve indexing) is also the preferred way to index ndarray or any numpy based tensors (either in PyTorch or TF) instead of using +ve indexing. This way you will always know the correct shapes.

Consider this example:

import torch
X = torch.arange(12).reshape((12))      ## X.shape = [12]
Y = torch.arange(12).reshape((1,12))    ## Y.shape = [1,12]
Z = X+Y                                 ## Z.shape = [1,12]

and contrast the above example with this below one

import torch
X = torch.arange(12).reshape((12))      ## X.shape = [12]
Y = torch.arange(12).reshape((12,1))    ## Y.shape = [12, 1]   <--- NOTE
Z = X+Y                                 ## Z.shape = [12,12]   <--- NOTE

And in both the above examples, a very simple rule is followed during broadcasting:

1. Start from RIGHT-to-LEFT indices (i.e. -ve indexing) instead of the conventional LEFT-to-RIGHT process.
2. If at any point, the shape values mismatch; check
   (2.1): If any of the two values are 1 then inflate this tensor in this axis with the OTHER value
   (2.2): Else, Throw ERROR(“dimension mismatch”)
3. Else, CONTINUE moving LEFT

Hope it helps.

CannedWalk

if anyone has any confusion related to broadcasting, this is how it actually looks in Numpy.
taken form python data science handbook

1 reply

Tatiane_Nogueira

I’ve checked this information, but I have obtained a different result:

1 reply

Tejas-Garhewal

1. Run the code in this section. Change the conditional statement X == Y to X < Y or X > Y, and then see what kind of tensor you can get.

X = torch.arange(15).reshape(5,3)

Y = torch.arange(15, 0, -1).reshape(5,3)

X == Y, X > Y, X < Y


(tensor([[False, False, False],
         [False, False, False],
         [False, False, False],
         [False, False, False],
         [False, False, False]]),
 tensor([[False, False, False],
         [False, False, False],
         [False, False,  True],
         [ True,  True,  True],
         [ True,  True,  True]]),
 tensor([[ True,  True,  True],
         [ True,  True,  True],
         [ True,  True, False],
         [False, False, False],
         [False, False, False]]))

2. Replace the two tensors that operate by element in the broadcasting mechanism with other shapes, e.g., 3-dimensional tensors. Is the result the same as expected?

X = torch.arange(8).reshape(4, 2, 1)
Y = torch.arange(8).reshape(1, 2 ,4)

print(f"{X}, \n\n\n{Y}, \n\n\n{X + Y}")


tensor([[[0],
         [1]],

        [[2],
         [3]],

        [[4],
         [5]],

        [[6],
         [7]]]), 


tensor([[[0, 1, 2, 3],
         [4, 5, 6, 7]]]), 


tensor([[[ 0,  1,  2,  3],
         [ 5,  6,  7,  8]],

        [[ 2,  3,  4,  5],
         [ 7,  8,  9, 10]],

        [[ 4,  5,  6,  7],
         [ 9, 10, 11, 12]],

        [[ 6,  7,  8,  9],
         [11, 12, 13, 14]]])

Yes, the result matches what I expected as well as with what I learned in this notebook

Gr8guns

Exercise-2. Replace the two tensors that operate by element in the broadcasting mechanism with other shapes, e.g., 3-dimensional tensors. Is the result the same as expected?

I understand this error in principle, but can someone clarify objectively what “non-singleton dimension” means?

c = torch.arange(6).reshape((3, 1, 2))
e = torch.arange(8).reshape((8, 1, 1))
c, e
(tensor([[[0, 1]],
 
         [[2, 3]],
 
         [[4, 5]]]),
 tensor([[[0]],
 
         [[1]],
 
         [[2]],
 
         [[3]],
 
         [[4]],
 
         [[5]],
 
         [[6]],
 
         [[7]]]))


c + e
---------------------------------------------------------------------------
RuntimeError                              Traceback (most recent call last)
Cell In [53], line 1
----> 1 c + e

RuntimeError: The size of tensor a (3) must match the size of tensor b (8) at non-singleton dimension 0

xavier_porras

in: (X>Y).dtype
out: torch.bool

in: X = torch.arange(12, dtype=torch.float32).reshape(3,4)
Y = torch.tensor([[1, 4, 3, 5]])
X.shape, Y.shape
(torch.Size([3, 4]), torch.Size([1, 4]))

Exp for broadcasting
Each tensor has at least one dimension.
When iterating over the dimension sizes, starting at the trailing dimension, the dimension sizes must either be equal, one of them is 1, or one of them does not exist.

ari

This code:
before = id(X)
X += Y
id(X) == before

Does not return true for me. I asked chatGPT it says this does not adjust the vairable in place.
What am I doing wrong?
Thanks!

EDIT: Is seems this only works with lists, not regular variables. Is this where I went wrong. Thanks!

1 reply

Ashkin

@ari can you check if both X and Y are tensors. It could be that your Y is a ndarray from numpy.

cclj

Ex1.

import torch

X = torch.arange(12, dtype=torch.float32).reshape((3,4))
Y = torch.tensor([[2.0, 1, 4, 3], [1, 2, 3, 4], [4, 3, 2, 1]])

X < Y

Output:

tensor([[ True, False,  True, False],
        [False, False, False, False],
        [False, False, False, False]])

X > Y

Output:

tensor([[False, False, False, False],
        [ True,  True,  True,  True],
        [ True,  True,  True,  True]])

• As expected, the operators > and < perform element-wise comparison operations on the two tensors with the same shape, as per the documentation.

Ex2.

• The broadcasting scheme expands the dimensions by copying the elements along length-1 axes, so that a binary operation can be feasible.
• Along each trailing dimension, the dimension sizes must either be: (1) equal, (2) one of them is 1, or (3) one of them does not exist.
• Take the example of and , then the addition of yields a tensor in shape (3, 3, 3) defined as

where is determined via

a = torch.arange(9).reshape((3, 1, 3))
b = torch.arange(3).reshape((1, 3, 1))
a, b

Output:

(tensor([[[0, 1, 2]],
 
         [[3, 4, 5]],
 
         [[6, 7, 8]]]),
 tensor([[[0],
          [1],
          [2]]]))

c = a + b
c

Output:

tensor([[[ 0,  1,  2],
         [ 1,  2,  3],
         [ 2,  3,  4]],

        [[ 3,  4,  5],
         [ 4,  5,  6],
         [ 5,  6,  7]],

        [[ 6,  7,  8],
         [ 7,  8,  9],
         [ 8,  9, 10]]])

# If not that straightforward to see, let's try an explicit broadcasting scheme.
c1 = torch.zeros((3, 3, 3))
for i in range(3):
    for j in range(3):
        for k in range(3):
            c1[i, j, k] = a[i, 0, k] + b[0, j, 0]
c1 - c

Output:

tensor([[[0., 0., 0.],
         [0., 0., 0.],
         [0., 0., 0.]],

        [[0., 0., 0.],
         [0., 0., 0.],
         [0., 0., 0.]],

        [[0., 0., 0.],
         [0., 0., 0.],
         [0., 0., 0.]]])

Nathan_Zorndorf

In Saving Memory the text mentions two reasons that creating new spaces in memory to store variables might be undesireable:

First, we do not want to run around allocating memory unnecessarily all the time. In machine learning, we often have hundreds of megabytes of parameters and update all of them multiple times per second. Whenever possible, we want to perform these updates in place . Second, we might point at the same parameters from multiple variables. If we do not update in place, we must be careful to update all of these references, lest we spring a memory leak or inadvertently refer to stale parameters.

I don’t understand the second reason. Can someone provide an example? When would you point at the same parameters from multiple variables and what does this look like?

iamyaa

np.ones() gives only ones as digits so the above diagram is not correct.
Here is a sample:

v=np.ones((3,1))
v
array ([[1.],
[1.],
[1.]])
check it out

polhuang

Thanks for including that. You can understand the concept instantly from the visual description.

Nathanael

import torch x=torch.arange(12,dtype=torch.float32).reshape(3,4) y=torch.tensor([[2, 6, 7, 8], [1, 2, 3, 4], [4, 3, 2, 1]]) x<y,x>y,x==y

(tensor([[ True, True, True, True],
[False, False, False, False],
[False, False, False, False]]),
tensor([[False, False, False, False],
[ True, True, True, True],
[ True, True, True, True]]),
tensor([[False, False, False, False],
[False, False, False, False],
[False, False, False, False]]))

filipv

I went through these exercises a week or so ago, but I recall:

1. X < Y or X > Y yields a boolean tensor which is the result of element-wise inequality operations.
2. I don’t recall being surprised, but I had already read through the PyTorch document on Broadcasting semantics. Of note – the tensors are aligned starting at the trailing dimension.

Sarah

Exercise 1

import torch

# Rewriting the tensors created in section 2.1.3 Operations
X = torch.arange(12, dtype=torch.float64).reshape((3, 4))
Y = torch.tensor([[2.0, 1, 4, 3], [1, 2, 3, 4], [4, 3, 2, 1]])
X, Y, X == Y, X < Y, X > Y

(tensor([[ 0.,  1.,  2.,  3.],
         [ 4.,  5.,  6.,  7.],
         [ 8.,  9., 10., 11.]], dtype=torch.float64),
 tensor([[2., 1., 4., 3.],
         [1., 2., 3., 4.],
         [4., 3., 2., 1.]]),
 tensor([[False,  True, False,  True],
         [False, False, False, False],
         [False, False, False, False]]),
 tensor([[ True, False,  True, False],
         [False, False, False, False],
         [False, False, False, False]]),
 tensor([[False, False, False, False],
         [ True,  True,  True,  True],
         [ True,  True,  True,  True]]))

Exercise 2

# Rewriting and modifying the tensors created in section 2.1.4 Broadcasting
a = torch.arange(12).reshape((2, 1, 6))
b = torch.arange(4).reshape((1, 4, 1))
c = a + b
a, b, c, a.shape, b.shape, c.shape

(tensor([[[ 0,  1,  2,  3,  4,  5]],
 
         [[ 6,  7,  8,  9, 10, 11]]]),
 tensor([[[0],
          [1],
          [2],
          [3]]]),
 tensor([[[ 0,  1,  2,  3,  4,  5],
          [ 1,  2,  3,  4,  5,  6],
          [ 2,  3,  4,  5,  6,  7],
          [ 3,  4,  5,  6,  7,  8]],
 
         [[ 6,  7,  8,  9, 10, 11],
          [ 7,  8,  9, 10, 11, 12],
          [ 8,  9, 10, 11, 12, 13],
          [ 9, 10, 11, 12, 13, 14]]]),
 torch.Size([2, 1, 6]),
 torch.Size([1, 4, 1]),
 torch.Size([2, 4, 6]))

Pen_Dora

1.

X = torch.arange(12, dtype=torch.float32).reshape((3,4))
Y = torch.tensor([[2.0, 1, 4, 3], [1, 2, 3, 4], [4, 3, 2, 1]])
print(X,Y,X==Y, X<Y, X>Y)

tensor([[ 0.,  1.,  2.,  3.],
        [ 4.,  5.,  6.,  7.],
        [ 8.,  9., 10., 11.]]) 

tensor([[2., 1., 4., 3.],
        [1., 2., 3., 4.],
        [4., 3., 2., 1.]]) 

tensor([[False,  True, False,  True],
        [False, False, False, False],
        [False, False, False, False]]) 

tensor([[ True, False,  True, False],
        [False, False, False, False],
        [False, False, False, False]]) 

tensor([[False, False, False, False],
        [ True,  True,  True,  True],
        [ True,  True,  True,  True]])

2.

a = torch.arange(3).reshape((3, 1))
b = torch.arange(2).reshape((1, 2))

a_3d = a.reshape((3,1,1))
b_3d = b.reshape((1,2,1))
print(a_3d, b_3d)
print(a_3d+b_3d)

tensor([[[0]],

        [[1]],

        [[2]]]) 

tensor([[[0],
         [1]]])

tensor([[[0],
         [1]],

        [[1],
         [2]],

        [[2],
         [3]]])

Looks correct, kindly tell me if something’s missing, I am new to this.

Lamhita_Prem

Chapter 2.1

1. X = torch.arange(12, dtype=torch.float32).reshape((3,4))
   Y = torch.tensor([[2.0, 1, 4, 3], [1, 2, 3, 4], [4, 3, 2, 1]])
   torch.cat((X, Y), dim=0)
   Output:
   tensor([[ 0., 1., 2., 3.],
   [ 4., 5., 6., 7.],
   [ 8., 9., 10., 11.],
   [ 2., 1., 4., 3.],
   [ 1., 2., 3., 4.],
   [ 4., 3., 2., 1.]])
   X > Y
   Output:
   tensor([[False, False, False, False],
   [ True, True, True, True],
   [ True, True, True, True]])
   X < Y
   tensor([[ True, False, True, False],
   [False, False, False, False],
   [False, False, False, False]])
   Where elements of the tensors are equal, it’s False, in both cases

2. Take 2 3D tensors:
   A = torch.tensor([[[1, 2]], [[3, 4]], [[5, 6]]])
   B = torch.tensor([[[1, 2], [3, 4]], [[5, 6], [7, 8]], [[9, 10], [11, 12]]])
   A + B
   Output:
   tensor([[[ 2, 4],
   [ 4, 6]],

    [[ 8, 10],
     [10, 12]],
   
    [[14, 16],
     [16, 18]]])
   

Explanation:
A’s shape is (3,1,2)
B’s shape is (3,2,2)

Before summing up, A is broadcasted along the 2nd dimension:
A = tensor([[[1, 2],[1,2]],

[[3, 4],[3, 4]],

[[5, 6],[5,6]]])

Then follows the usual element-by-element summation

amaze1111

Why is it not broadcasting?

hhllhhyyds

using candle in Rust to show Tensor data manipulation

use candle_core::{Device, Tensor};

fn main() -> Result<(), Box<dyn std::error::Error>> {
    let cpu = Device::Cpu;

    let g = Tensor::arange::<f32>(0., 12., &cpu)?;
    println!("cpu g = {g}");

    let g = g.reshape((3, 4))?;

    let gpu = Device::new_metal(0)?;
    let x = Tensor::arange::<f32>(0., 12., &gpu)?;
    println!("metal x = {x}");

    println!("x element count = {}", x.elem_count());

    println!("x shape = {:?}", x.shape());

    let x = x.reshape((3, 4))?;

    println!("x after reshape is\n{}, shape is {:?}", x, x.shape());

    let zeros_tensor = Tensor::zeros((2, 3, 4), candle_core::DType::F32, &cpu)?;
    println!("tensor zeros:\n{}", zeros_tensor);

    println!(
        "tensor ones:\n{}",
        Tensor::ones((2, 3, 4), candle_core::DType::F32, &cpu)?
    );

    println!("tensor random:\n{}", Tensor::randn(0.0, 1.0, (3, 4), &cpu)?);

    println!(
        "tensor specified:\n{}",
        Tensor::new(&[[2_i64, 1, 4, 3], [1, 2, 3, 4], [4, 3, 2, 1]], &cpu)?
    );

    println!("x[-1] = {:?}", x.get(2)?.to_vec1::<f32>()?);
    println!(
        "x[1:3] = {:?}",
        x.index_select(&Tensor::new(&[1_i64, 2], &gpu)?, 0)?
            .to_vec2::<f32>()?
    );

    x.get(1)?.slice_set(&Tensor::new(&[17_f32], &gpu)?, 0, 2)?;
    println!("x = \n{}", x);

    let y = Tensor::from_slice(&[12_f32; 8], (2, 4), &gpu)?;
    let x = x.slice_assign(&[0..2, 0..4], &y)?;
    println!("x = \n{}", x);

    let z = x.to_device(&cpu)?;
    println!("x exp = \n{}", x.exp()?);
    println!("z exp = \n{}", z.exp()?);

    let p = Tensor::from_slice(&[1_f32, 2., 4., 8.], (1, 4), &gpu)?;
    let q = Tensor::from_slice(&[2_f32; 4], (1, 4), &gpu)?;

    println!("p = {p},\nq = {q}");

    println!("p + q = {}", (p.clone() + q.clone())?);
    println!("p - q = {}", (p.clone() - q.clone())?);
    println!("p * q = {}", (p.clone() * q.clone())?);
    println!("p / q = {}", (p.clone() / q.clone())?);
    println!("p ** q = {}", (p.clone().pow(&q))?);

    let gz0 = Tensor::cat(&[g.clone(), z.clone()], 0)?;
    let gz1 = Tensor::cat(&[g.clone(), z.clone()], 1)?;

    println!("gz0 = \n{gz0}");
    println!("gz1 = \n{gz1}");

    println!("z == g:\n{}", z.eq(&g)?);

    println!("z < g:\n{}", z.lt(&g)?);

    println!("g sum = {}", g.sum_all()?);

    let a = Tensor::arange(0_i64, 3, &gpu)?.reshape((3, 1))?;
    println!("a = \n{a}");

    let b = Tensor::arange(0_i64, 2, &gpu)?.reshape((1, 2))?;
    println!("b = \n{b}");

    println!("a + b = \n{}", a.broadcast_add(&b)?);

    Ok(())
}