This is probably carried over from the MXNET version, where the corresponding operation does create a copy:
asnumpy() : Returns anumpy.ndarrayobject with value copied from this array.
@anirudh should be able to confirm/deny this.
Thanks, @Aaron and @gphilip for raising this. Most part of the book has common text and we are trying to fix issues like these where the frameworks differ in design. Feel free to raise any other issues if you find something similar in other sections on the forum or the Github repo. Really appreciate it!
This will be fixed in the next release.
1 Like
e = torch.arange(12).reshape(2, -1, 6)
f = torch.tensor([1, 2, 3, 4]).reshape(-1, 4, 1)
e, f, e.shape, f.shape
(tensor([[[ 0, 1, 2, 3, 4, 5]],
[[ 6, 7, 8, 9, 10, 11]]]), tensor([[[1],
[2],
[3],
[4]]]), torch.Size([2, 1, 6]), torch.Size([1, 4, 1]))
e + f
tensor([[[ 1, 2, 3, 4, 5, 6],
[ 2, 3, 4, 5, 6, 7],
[ 3, 4, 5, 6, 7, 8],
[ 4, 5, 6, 7, 8, 9]],
[[ 7, 8, 9, 10, 11, 12],
[ 8, 9, 10, 11, 12, 13],
[ 9, 10, 11, 12, 13, 14],
[10, 11, 12, 13, 14, 15]]])
Hello! I had two questions from this section:
-
Where does the term “lifted” come from? I understand “lifted” means some function that operate on real numbers (scalars) can be “lifted” to a higher dimensional or vector operations. I was just curious if this is a commonly used term in mathematics.
-
Is there a rule for knowing what the shape of a broadcasted operation may be? For Exercise #2, I tried a shape of (3, 1, 1) + (1, 2, 1) to get (3, 2, 1). I also tried (3, 1, 1, 1) + (1, 2, 1) and got (3, 1, 2, 1). It kind of gets harder to visualize how broadcasting will work beyond 3-D, so I was wondering if someone could explain why the 2nd broad operation has the shape that it has intuitively.
Thank you very much!
Lifting is commonly used for this operation in functional programming (e.g. in Haskell), probably it has some roots in lambda calculus.
1 Like
@hojaelee , During broadcasting the shape matching of the two inputs X, Y happen in reverse order i.e. starting from the -1 axis. This (i.e. -ve indexing) is also the preferred way to index ndarray or any numpy based tensors (either in PyTorch or TF) instead of using +ve indexing. This way you will always know the correct shapes.
Consider this example:
import torch
X = torch.arange(12).reshape((12)) ## X.shape = [12]
Y = torch.arange(12).reshape((1,12)) ## Y.shape = [1,12]
Z = X+Y ## Z.shape = [1,12]
and contrast the above example with this below one
import torch
X = torch.arange(12).reshape((12)) ## X.shape = [12]
Y = torch.arange(12).reshape((12,1)) ## Y.shape = [12, 1] <--- NOTE
Z = X+Y ## Z.shape = [12,12] <--- NOTE
And in both the above examples, a very simple rule is followed during broadcasting:
- Start from RIGHT-to-LEFT indices (i.e. -ve indexing) instead of the conventional LEFT-to-RIGHT process.
- If at any point, the shape values mismatch; check
(2.1): If any of the two values are1then inflate this tensor in this axis with the OTHER value
(2.2): Else, Throw ERROR(“dimension mismatch”) - Else, CONTINUE moving LEFT
Hope it helps.
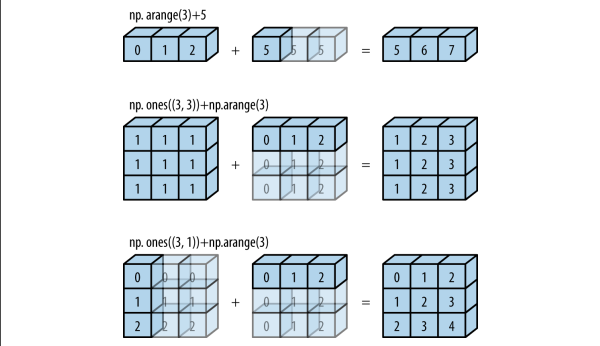
if anyone has any confusion related to broadcasting, this is how it actually looks in Numpy.
taken form python data science handbook
2 Likes
I’ve checked this information, but I have obtained a different result:
1. Run the code in this section. Change the conditional statement X == Y to X < Y or X > Y, and then see what kind of tensor you can get.
X = torch.arange(15).reshape(5,3)
Y = torch.arange(15, 0, -1).reshape(5,3)
X == Y, X > Y, X < Y
(tensor([[False, False, False],
[False, False, False],
[False, False, False],
[False, False, False],
[False, False, False]]),
tensor([[False, False, False],
[False, False, False],
[False, False, True],
[ True, True, True],
[ True, True, True]]),
tensor([[ True, True, True],
[ True, True, True],
[ True, True, False],
[False, False, False],
[False, False, False]]))
2. Replace the two tensors that operate by element in the broadcasting mechanism with other shapes, e.g., 3-dimensional tensors. Is the result the same as expected?
X = torch.arange(8).reshape(4, 2, 1)
Y = torch.arange(8).reshape(1, 2 ,4)
print(f"{X}, \n\n\n{Y}, \n\n\n{X + Y}")
tensor([[[0],
[1]],
[[2],
[3]],
[[4],
[5]],
[[6],
[7]]]),
tensor([[[0, 1, 2, 3],
[4, 5, 6, 7]]]),
tensor([[[ 0, 1, 2, 3],
[ 5, 6, 7, 8]],
[[ 2, 3, 4, 5],
[ 7, 8, 9, 10]],
[[ 4, 5, 6, 7],
[ 9, 10, 11, 12]],
[[ 6, 7, 8, 9],
[11, 12, 13, 14]]])
Yes, the result matches what I expected as well as with what I learned in this notebook
Exercise-2. Replace the two tensors that operate by element in the broadcasting mechanism with other shapes, e.g., 3-dimensional tensors. Is the result the same as expected?
I understand this error in principle, but can someone clarify objectively what “non-singleton dimension” means?
c = torch.arange(6).reshape((3, 1, 2))
e = torch.arange(8).reshape((8, 1, 1))
c, e
(tensor([[[0, 1]],
[[2, 3]],
[[4, 5]]]),
tensor([[[0]],
[[1]],
[[2]],
[[3]],
[[4]],
[[5]],
[[6]],
[[7]]]))
c + e
---------------------------------------------------------------------------
RuntimeError Traceback (most recent call last)
Cell In [53], line 1
----> 1 c + e
RuntimeError: The size of tensor a (3) must match the size of tensor b (8) at non-singleton dimension 0
in: (X>Y).dtype
out: torch.bool
in: X = torch.arange(12, dtype=torch.float32).reshape(3,4)
Y = torch.tensor([[1, 4, 3, 5]])
X.shape, Y.shape
(torch.Size([3, 4]), torch.Size([1, 4]))
Exp for broadcasting
Each tensor has at least one dimension.
When iterating over the dimension sizes, starting at the trailing dimension, the dimension sizes must either be equal, one of them is 1, or one of them does not exist.
This code:
before = id(X)
X += Y
id(X) == before
Does not return true for me. I asked chatGPT it says this does not adjust the vairable in place.
What am I doing wrong?
Thanks!
EDIT: Is seems this only works with lists, not regular variables. Is this where I went wrong. Thanks!
Ex1.
import torch
X = torch.arange(12, dtype=torch.float32).reshape((3,4))
Y = torch.tensor([[2.0, 1, 4, 3], [1, 2, 3, 4], [4, 3, 2, 1]])
X < Y
Output:
tensor([[ True, False, True, False],
[False, False, False, False],
[False, False, False, False]])
X > Y
Output:
tensor([[False, False, False, False],
[ True, True, True, True],
[ True, True, True, True]])
- As expected, the operators
>and<perform element-wise comparison operations on the two tensors with the same shape, as per the documentation.
Ex2.
- The broadcasting scheme expands the dimensions by copying the elements along length-1 axes, so that a binary operation can be feasible.
- Along each trailing dimension, the dimension sizes must either be: (1) equal, (2) one of them is 1, or (3) one of them does not exist.
- Take the example of
and 
, then the addition of 
yields a tensor in shape (3, 3, 3)defined as
where 
is determined via
a = torch.arange(9).reshape((3, 1, 3))
b = torch.arange(3).reshape((1, 3, 1))
a, b
Output:
(tensor([[[0, 1, 2]],
[[3, 4, 5]],
[[6, 7, 8]]]),
tensor([[[0],
[1],
[2]]]))
c = a + b
c
Output:
tensor([[[ 0, 1, 2],
[ 1, 2, 3],
[ 2, 3, 4]],
[[ 3, 4, 5],
[ 4, 5, 6],
[ 5, 6, 7]],
[[ 6, 7, 8],
[ 7, 8, 9],
[ 8, 9, 10]]])
# If not that straightforward to see, let's try an explicit broadcasting scheme.
c1 = torch.zeros((3, 3, 3))
for i in range(3):
for j in range(3):
for k in range(3):
c1[i, j, k] = a[i, 0, k] + b[0, j, 0]
c1 - c
Output:
tensor([[[0., 0., 0.],
[0., 0., 0.],
[0., 0., 0.]],
[[0., 0., 0.],
[0., 0., 0.],
[0., 0., 0.]],
[[0., 0., 0.],
[0., 0., 0.],
[0., 0., 0.]]])
In Saving Memory the text mentions two reasons that creating new spaces in memory to store variables might be undesireable:
First, we do not want to run around allocating memory unnecessarily all the time. In machine learning, we often have hundreds of megabytes of parameters and update all of them multiple times per second. Whenever possible, we want to perform these updates in place . Second, we might point at the same parameters from multiple variables. If we do not update in place, we must be careful to update all of these references, lest we spring a memory leak or inadvertently refer to stale parameters.
I don’t understand the second reason. Can someone provide an example? When would you point at the same parameters from multiple variables and what does this look like?
np.ones() gives only ones as digits so the above diagram is not correct.
Here is a sample:
v=np.ones((3,1))
v
array ([[1.],
[1.],
[1.]])
check it out
Thanks for including that. You can understand the concept instantly from the visual description.
import torch x=torch.arange(12,dtype=torch.float32).reshape(3,4) y=torch.tensor([[2, 6, 7, 8], [1, 2, 3, 4], [4, 3, 2, 1]]) x<y,x>y,x==y
(tensor([[ True, True, True, True],
[False, False, False, False],
[False, False, False, False]]),
tensor([[False, False, False, False],
[ True, True, True, True],
[ True, True, True, True]]),
tensor([[False, False, False, False],
[False, False, False, False],
[False, False, False, False]]))
I went through these exercises a week or so ago, but I recall:
X < YorX > Yyields a boolean tensor which is the result of element-wise inequality operations.- I don’t recall being surprised, but I had already read through the PyTorch document on Broadcasting semantics. Of note – the tensors are aligned starting at the trailing dimension.
Exercise 1
import torch
# Rewriting the tensors created in section 2.1.3 Operations
X = torch.arange(12, dtype=torch.float64).reshape((3, 4))
Y = torch.tensor([[2.0, 1, 4, 3], [1, 2, 3, 4], [4, 3, 2, 1]])
X, Y, X == Y, X < Y, X > Y
(tensor([[ 0., 1., 2., 3.],
[ 4., 5., 6., 7.],
[ 8., 9., 10., 11.]], dtype=torch.float64),
tensor([[2., 1., 4., 3.],
[1., 2., 3., 4.],
[4., 3., 2., 1.]]),
tensor([[False, True, False, True],
[False, False, False, False],
[False, False, False, False]]),
tensor([[ True, False, True, False],
[False, False, False, False],
[False, False, False, False]]),
tensor([[False, False, False, False],
[ True, True, True, True],
[ True, True, True, True]]))
Exercise 2
# Rewriting and modifying the tensors created in section 2.1.4 Broadcasting
a = torch.arange(12).reshape((2, 1, 6))
b = torch.arange(4).reshape((1, 4, 1))
c = a + b
a, b, c, a.shape, b.shape, c.shape
(tensor([[[ 0, 1, 2, 3, 4, 5]],
[[ 6, 7, 8, 9, 10, 11]]]),
tensor([[[0],
[1],
[2],
[3]]]),
tensor([[[ 0, 1, 2, 3, 4, 5],
[ 1, 2, 3, 4, 5, 6],
[ 2, 3, 4, 5, 6, 7],
[ 3, 4, 5, 6, 7, 8]],
[[ 6, 7, 8, 9, 10, 11],
[ 7, 8, 9, 10, 11, 12],
[ 8, 9, 10, 11, 12, 13],
[ 9, 10, 11, 12, 13, 14]]]),
torch.Size([2, 1, 6]),
torch.Size([1, 4, 1]),
torch.Size([2, 4, 6]))