Q1感觉可以理解为权重矩阵为对角矩阵的全连接层
我的理解(不知道对不对)是这个地方是在证明卷积和全连接的区别(注意下标被重新索引了),当更换需要得到的像素位置的时候,全连接的权重也会有改变(会去使用新的像素位置的权重),为了实现平移不变性Vab相当于卷积核的权重,这样当卷积核移动的时候,权重是共享的。
我不太理解6.1.1式中的W为什么是四阶权重张量,有人可以给我解答一下嘛?万分感谢!
你可以把[W]i,j,k,l的值看作是参数为i,j,k,l的四元函数。由于k=a+i, l=b+j, 即k和l也可以用i,j,a,b表示,即也可以将其看作i,j,a,b的四元函数,因此可以存在另一个四元函数[V]i,j,a,b,当满足k=a+i, l=b+j时,[V]i,j,a,b其值与[W]i,j,k,l相同。你的误区在于直接将对应的W和V的一对元素的下标等同起来了。或者换个说法,如果把k=a+i和l=b+j写成k=f(a, i),l=g(b, j),[W]i,j,k,l = [W]i,j,f(a, i),g(b, j),再将其写成以i,j,a,b为变量的四元函数,则是[V]i,j,a,b,因此二者之间存在双射关系,但不是恒等映射。希望对你有帮助。
其实可以把这里的四阶张量理解为四元函数。确定是几阶张量就是要确定函数有几个自由度。因为以传统全连接层的视角,要确定隐藏层中一个点的值,需要以原图中的一个点(i, j)为中心加权处理周围某个范围内的一整片像素值,只考虑单通道的情况下,权重矩阵需要对这一整片图像里的每一个点的像素加一个权重值,因此一个权重值需要四个变量来确定,即中心的位置i,j,以及周围的某个像素的绝对坐标k和l。如果把k和l用相对于(i, j)的相对坐标来写的话即a, b,权重矩阵就从[W]i,j,k,l变成了[V]i,j,a,b。后面加入平移不变性,所以i,j这两个参数就不需要了,因为只要a和b确定,对任何i, j,函数的值都不变化。而局部性就是控制了相对位移a和b的范围,并不需要遍历整张图像,而是只计算中心点附近的一块。
不好意思,我的数学很差,想问下这个三角形符号代表啥意思,,,,
那是一个数学符号delta 在这里代表一个阈值
原来如此,感谢解答~,数学都忘的差不多了,哈哈~
这里所说的“只是形式上的转变”感觉有点误导读者,这里感觉是把W.shape[-2:]=X.shape变为了W.shape[-2:]=X.shape or W.shape[-2:]!=X.shape,W的形状就从原本单一的形状变成了各种各样的形状,而此时的X和H就不一定具有相同的形状,这与上文的
相冲突
Q2: 为什么平移不变性可能也不是好主意呢?
个人认为除非是人为的像素级别的操作或数据增强,世界上任意两张照片没有严格的平移不变性。
我们通常意义上的平移不变性是后从宏观上认为的。
参考 https://browse.arxiv.org/pdf/1805.12177.pdf
该文章也像 @DJ_Zhu 所说,卷积的平移不变性有争议,
或者说卷积在设计时确实考虑了平移不变性,但由于卷积和池化操作有步长和范围限制,卷积只有对特定长度(大致理解为各卷积核步长的最小公倍数)倍数的物体平移有不变性
总结认为卷积在落实平移不变性时落实得非常差,卷积核越多,也就是网络越大,平移不变性越差。
这里其实是将全连接层往卷积层上引导,你将V看成是随位置(i,j)变化的卷积核就好理解了
我的理解是是分量对应相乘,四个角标索引就是一个scaler了
二维张量哪里来的通道,带有通道的是三维张量好吧,作者的意思是这个二维张量就是一个通道,图像的是三个维度是长宽通道数,你把其中一个通道拿出来不就是一个二维的张量…
请问(6.1.7)加入的第四个坐标被用来表示了什么?还是说仅仅是写在上面?
6.1.6的那个公式不是Q6的证明吧?它只是一个从单一参数a到两个参数(a, b)的扩展。证明应该是利用u = x - z 然后简单substitute一下u。
说的太对了,不过我觉着这个平移不变性,这里讲的应该是一种很理想的情况,即检测目标所处的背景比较简单且分布均匀,因为只有这样,目标移动前后的图像与核运算才能在输出上近似平移。当然如果加上第二个局部性,使得输出中的i ,j代表的像素取决于输入对应位置周围的像素加权求和,则可以很大程度上使得背景不需要那么简单与分布均匀,因为在增加局部约束时,自然而然选取的范围主要以小范围为主,当目标在这个小范围内时,背景影响将会很少,因此这个局部大小的选择我觉着很影响最终结果。(个人理解,不知道对不对)
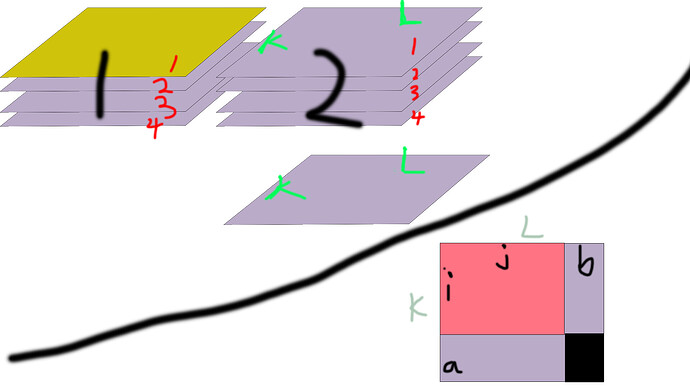
我自己对公式(6.1.1)的理解
第一步公式
四阶矩阵(黑色标号是一维、红色是二维、绿色是三四维)
四阶矩阵的三四维与二阶矩阵一二维元素分别相乘再求和得出输出二维矩阵的其中一个元素,因此最后的输出是(2,4)的矩阵
第二步公式
右下角是我对第二步的理解,但是感觉不能和第一步相等啊,对于输出的(i,j)元素,二维矩阵只有黑色部分参与了运算,而第一步整个矩阵都参与了运算,是我整个都理解错了吗? ![]()
个人理解,v是卷积核,其大小和图像大小不必相同,其权重系数在平移时可以重复使用;w是所有权重系数的集合,其尺寸应该是和图像一致的。换句话说,v在整个图像上游走时的轨迹构成的权重矩阵就是w。