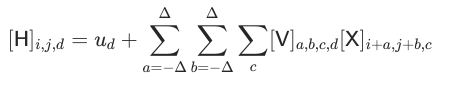从全连接层到卷积

中文版
#1

https://zh.d2l.ai/chapter_convolutional-neural-networks/why-conv.html

#2

"因此，我们可以把隐藏表示想象为一系列具有二维张量的 通道 （channel）。"正常的语序不应该是“ 一系列具有 通道（channel）的二维张量”吗？

1 Like
#3

虽然中文表述还是怪怪的，但是这一节讲的非常好！motivation和逻辑非常清晰！

#4

在6.1.2. 多层感知机的限制中，W变成V的过程中，W的下标由k,l变成a,b，X的下标k,l变成i+a,j+b，于是k=a,l=b；k=i+a,l=j+b,这不存在矛盾吗？

#5

请问在哪找课后练习的答案
Please ask in where find after-class practice’s answer.

#6

V 和 W 不是同样的张量，它们只是有着一一对应的关系

#7

我感觉翻译的很好。只是这一节要多读几遍才能理解。反复的看几遍就有一种豁然开朗的感觉

#8

从全连接到卷积有种：（1）权重的独立到共享（2）全局到局部的感觉

#9

我不能理解W 与 Ｘ是怎么具体运算的，一个四阶ｔｅｎｓｏｒ与 ２阶 ｔｅｎｓｏｒ相乘，还是是我的理解有问题

#10

张量运算之间的广播机制，我觉得是这样，可能不对

#11

你是对的，但这里究竟是对应元素相乘，还是矩阵的乘法呢。

#12

能通俗地阐述一下吗，还是不能理解，谢谢您！

#13

你好！我知道这里是怎么运算的了谢谢，但我还有一个疑惑：在6.1.2. 多层感知机的限制中，W变成V的过程中，W的下标由k,l变成a,b，X的下标k,l变成i+a,j+b，于是k=a,l=b；k=i+a,l=j+b,这不存在矛盾吗？这个问题的回答我没有理解，可以解答一下吗

#14

我是这样理解的，i，j 给定了，所以W也是一个二阶的

#15

感觉是两个公式确实不能划等号，第一个式子随着i变化卷积区域都不变，都是k、j，但第二个式子随着i变化，卷积的区域变了，是i+a，j+b。

#16
  1. 内部像素可以卷积它周围的像素，边界的像素本应卷积的范围会超出图像。如果获取隐藏表示是为了提取特征，那么特征从内部像素提取和从边界像素提取是否应赋予同等机会，怎么算同等，问题最终归结于：在无法维持相同形状卷积范围的情况下如何改变隐藏表示对应像素的计算式。
    1. 音频、文本都是一维的数据，不能卷积一个矩形范围，可以卷积前后几个元素。具体适不适合还要看任务，适合的不适合的肯定都是有的。
#17

3.看下一节说
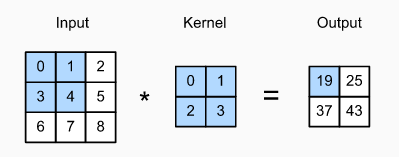
image

The height and width of the kernel are both 2. The shape of the kernel window (or convolution window ) is given by the height and width of the kernel (here it is 2×2).
注意到kernel和kernel window说得不是一样东西，意思就是隐藏表示比原图像形状小一圈，边界一圈在隐藏表示里直接没了，就不需要想怎么计算了。觉得这样挺好的，不然边界像素怎么映射还要根据具体任务调整，这下就只需要记得别把特征放在边界上就行了。。。

#18

又说维持大小不变的方法是填充0。觉得如果绝对值小是被需要的特征，那这种做法就是提高了边界的优先级。。

#19

Hi，关于公式：(6.1.7)
应该是缺少了一个偏置吧，应该加上相应的通道偏置：
image

1 Like
#20

Q1: 假设卷积层(6.1.3)覆盖的局部区域delta=0。在这种情况下，证明卷积内核为每组通道独立地实现一个全连接层。
A1: 实际就是问，1×1的卷积核是否等价于全连接（参见NiN网络结构）。个人比较赞同的一个回答：卷积核为1×1且步长为1的卷积层可以代替全连接层这个表述有一定的误导性， 表达为上一层是全连接层的全连接层可以转化为卷积核为1×1的卷积层更合适些；而上一层是卷积层的全连接层可以转化为卷积核为h×w的卷积层，h和w分别为上一层卷积层的高和宽。
参考链接：1*1的卷积核和全连接层有什么异同？ - 知乎

# 代码验证
import torch
import torch.nn as nn


class MyNet1(nn.Module):
    def __init__(self, linear1, linear2):
        super(MyNet1, self).__init__()
        self.linear1 = linear1
        self.linear2 = linear2

    def forward(self, X):
        return self.linear2(self.linear1(nn.Flatten()(X)))


class MyNet2(nn.Module):
    def __init__(self, linear, conv2d):
        super(MyNet2, self).__init__()
        self.linear = linear
        self.conv2d = conv2d

    def forward(self, X):
        X = self.linear(nn.Flatten()(X))
        X = X.reshape(X.shape[0], -1, 1, 1)
        X = nn.Flatten()(self.conv2d(X))
        return X


linear1 = nn.Linear(15, 10)
linear2 = nn.Linear(10, 5)
conv2d = nn.Conv2d(10, 5, 1)
linear2.weight = nn.Parameter(conv2d.weight.reshape(linear2.weight.shape))
linear2.bias = nn.Parameter(conv2d.bias)
net1 = MyNet1(linear1, linear2)
net2 = MyNet2(linear1, conv2d)
X = torch.randn(2, 3, 5)
# 两个结果实际存在一定的误差，直接print(net1(X) == net2(X))得到的结果不全是True
print(net1(X))
print(net2(X))

Q2: 为什么平移不变性可能也不是好主意呢？
A2: 先问是不是，再问为什么。关于卷积层的平移不变性，其实是有争议的，例如论文 https://arxiv.org/pdf/1805.12177.pdf 就提出过当小尺寸图像发生平移后，CNN会出现识别错误的现象，而且这一现象是普遍的，所以卷积层只是直观上存在平移不变性，你可以认为就算目标位置变了，经过相同卷积核提取的特征该有的都有，只是在最终结果中的位置顺序变了，但卷积层的平移不变性是有限的。（开放性问题，见仁见智）

Q3: 当从图像边界像素获取隐藏表示时，我们需要思考哪些问题？
A3: 需要考虑是否填充padding，以及填充多大的padding的问题

Q4: 描述一个类似的音频卷积层的架构。
A4: 一种基于卷积神经网络的音频特征生成方法，首先对声音信号进行预处理和离散傅里叶变换计算声音信号的幅度谱，形成二维谱图信号；然后搭建以上述二维谱图信号为输入的一维卷积神经网络并进行模型训练，得到特征生成器模型；最后对待测声音进行预处理和离散傅里叶变换得到二维谱图信号，并将其送入训练好的一维卷积神经网络，通过卷积网络计算，得到输出即为所要生成的音频特征，实现声音信号的音频特征生成。

Q5: 卷积层也适合于文本数据吗？为什么？
A5: 参考论文Convolutional Neural Networks for Sentence Classification
相关链接：卷积神经网络应用于文本分类原理简介 - 知乎
论文链接：[1408.5882] Convolutional Neural Networks for Sentence Classification

Q6: 证明在(6.1.6)中，fg=gf。
A6: 略