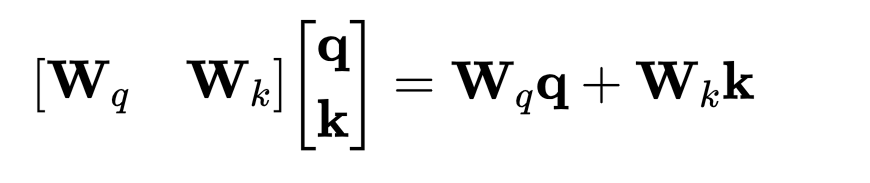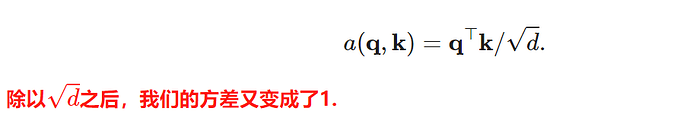为什么要除以根号d,而不是直接除以d呢?
人傻了,标准化的公式就是除以标准差,而d是方差,所以要开平方。属于是自问自答了。
def masked_softmax(X, valid_lens):
"""通过在最后一个轴上掩蔽元素来执行softmax操作"""
# X:3D张量,valid_lens:1D或2D张量
if valid_lens is None:
return nn.functional.softmax(X, dim=-1)
else:
shape = X.shape
if valid_lens.dim() == 1:
valid_lens = torch.repeat_interleave(valid_lens, shape[1])
else:
valid_lens = valid_lens.reshape(-1)
# 最后一轴上被掩蔽的元素使用一个非常大的负值替换,从而其softmax输出为0
X = d2l.sequence_mask(X.reshape(-1, shape[-1]), valid_lens,
value=-1e6)
return nn.functional.softmax(X.reshape(shape), dim=-1)
valid_lens = torch.repeat_interleave(valid_lens, shape[1])这一行的shape[1]应该改成shape[0]
我理解错了,就应该复制shape[1]次
假设随机变量X,Y是均值E(X),E(Y)为0,方差D(X),D(Y)为1,则令Z =XY,E(Z)=E(XY)=E(X)E(Y)=0,E(Z²)=E(X²Y²)=E(X²)E(Y²)=(E(X)²-D(X))(E(Y)²-D(Y))=D(X)D(Y),所以D(Z)=D(XY)=E(X²Y²)-E(XY)²=E(X²Y²)=D(X)D(Y)=1.
长度为d的两个向量点乘,相当于d个上述结果相加,上述推导是对应元素相乘形成的随机变量的均值与方差,则两个向量点乘,有D(Z1+…+Zd)=E([Z1+…+Zd]²)-E(Z1+…+Zd)²=E(Z1²+…+Zd²+Z1Z2…Z1Zd)-0=E(Z1²+…+Zd²)=dD(Z)=d
感觉还是要通过矩阵乘法将queries和keys转换到一个特征维度上来
个人理解:
我们的目的是要计算q和k之间的相关性然后再对v加权,加法和点积都可以做到相关性的计算,合并的话没有实现相关的计算,无法得到q和v之间的相关性,且维度改变,每一个查询头没有键值对的维度,需再进行转换才能对v加权
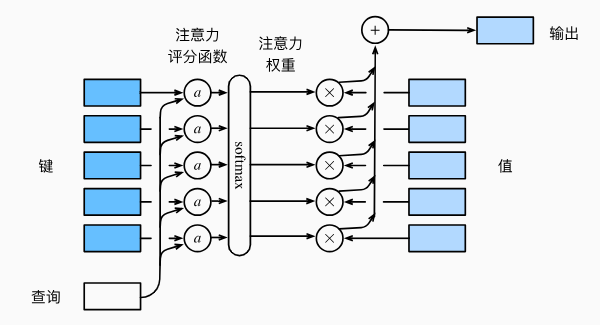
我对键、值、查询的理解是这样的:
假如我在找工作,我对入职某家公司后我每个月能拿到多少钱很好奇,这公司里不同级别不同学历的员工告诉我他们每个月拿了多少钱,我需要根据我的自身情况与这些员工的情况来推测我以后能拿到多少钱。这里我的自身情况(我的学历、我的工作经验、我的技能掌握情况等)就是查询,而员工A的个人情况就是一个key,员工A的工资就是这个key对应的value,员工A的情况-员工A的工资就是一个键值对,对于员工B、员工C等等也有他们对应的键值对。了解了这些情况之后,我肯定不能简单地把这些员工的工资平均下来作为我的期望工资,因为本科毕业、工作经验1年的我肯定比不上博士后、工作经验10年的老员工,那么我就需要一套评价指标来为不同员工的工资分配不同的权重,这套评价指标要考虑我的情况与不同员工的情况之间的差距,这就是注意力评分函数的作用,用来评价查询和键之间的相似程度,与查询越相似的键就为其分配越高的权重,在这个例子当中就是和我情况越相似的员工,对我的参考价值越大。最后把所有的权重与每个员工的工资相乘再求和,就得到了我的期望工资。
![]() 希望我的理解是对的
希望我的理解是对的
tanh 提供非线性特征变换,softmax 将原始分数转换的权重分布(概率分布)
很生动的理解,这是一个很好的例子 ![]()
紫薯布丁紫薯布丁紫薯布丁
我有点不太理解masked_softmax这个函数中对sequence_mask的使用。如果输入的X是三维,(batch_size, num_steps, feature_size), mask应该是在对num_steps这一维做mask吧,但是如
X = d2l.sequence_mask(X.reshape(-1, shape[-1]), valid_lens, value=-1e6)
这一行代码中,把X展平了,这时Xshape的1维就变成了feature_size,sequence_mask函数中的maxlen也对应改变,这一步是不是有点问题?
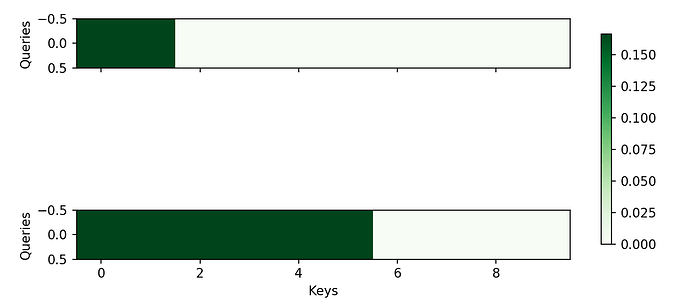
我确实不太理解,在加性注意力那一小结里,query和key的第一个维度为什么非得相同呢?我把第一个维度batch_size理解为num_queries和num_train,那么不相同也可以吧。同时还有画出来的注意力heatmap为什么会是2*10呢?就是代码一步步可以看出来数据形状怎么变的,但是在原理上我不太理解
我又去看了下视频教程,发现第一维度就是batch_size,跟num_queries和num_keys啥关系都没有,第二个维度才是num_queries和num_keys,那heatmap是不是画错了呢?会不会应该画两张热力图呢?因为batch_size = 2所以是画两张,同时因为num_queries = 1,num_keys = 10,那大小应该是1*10吧。我认为的应该如下图:
前面rnn的内容里面,batch_size之后还有个num_steps的维度,就是序列长度