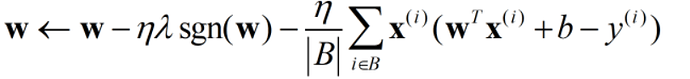Why does the Loss value increase monotonically after the learning rate increases by an order of magnitude to 0.03?
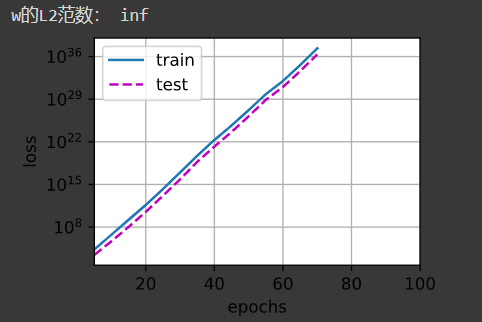
Since the squared loss function is a quadratic function, when the learning rate is large, the step size is large, resulting in a larger loss value the more iterative the neural network is.
我一开始也出现这个问题,后来发现lr少打了一个0,设置为0.003就好了
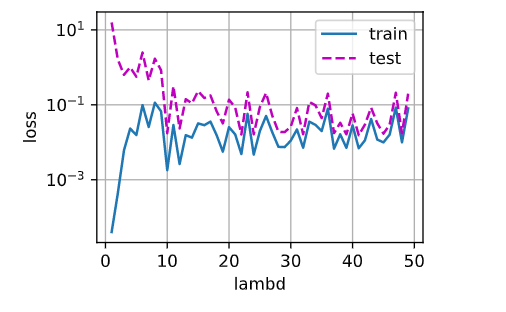
第一题,x为lambd,y为loss
不是的,我把本章的噪声去掉了,实验结果几乎不变,没有噪声依旧会有显著的过拟合现象,此时使用权重衰减一样可以有效控制过拟合
2、3段的讨论没看明白,每个字都认识。不过,加入这两段,有个好处,拖慢了看书速度,让我们可以多思考。
"""第一问"""
import numpy as np
lambds = np.arange(1,1000,10)
lambds = np.hstack(([0, 0.01, 0.1, 0.5],lambds))
def lambd_loss(wd):
loss_ = []
net = nn.Sequential(nn.Linear(num_inputs,1))
for param in net.parameters():
param.data.normal_()
loss = nn.MSELoss(reduction='none')
epochs, lr = 100, 0.003
trainer = torch.optim.SGD([
{"params":net[0].weight,'weight_decay':wd},
{"params":net[0].bias}],lr=lr)
for epoch in range(epochs):
for x, y in train_iter:
trainer.zero_grad()
l = loss(net(x),y)
l.mean().backward()
trainer.step()
loss_.append([d2l.evaluate_loss(net, train_iter, loss),
d2l.evaluate_loss(net, test_iter, loss)])
return loss_
loss_s = []
for lambd in lambds:
loss_s.append(lambd_loss(lambd))
loss_s = np.array(loss_s)
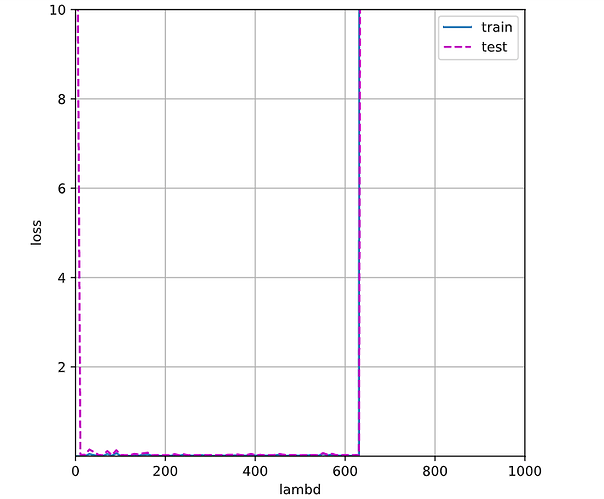
d2l.plot(lambds, [loss_s[:,:,0],loss_s[:,:,1]],'lambd','loss',
legend=['train','test'],xlim=[0,1000],ylim=[1e-4,10],figsize=(6,6))
# 可以看到lambd过小或过大,模型过拟合或欠拟合程度越大。介于两者之间出于振荡,无影响
你好 ,能分享一下代码么,不会画这个图0.0
请问L2惩罚导数的和等于和的导数是什么意思?
同求,这个loss是最终训完的loss吗
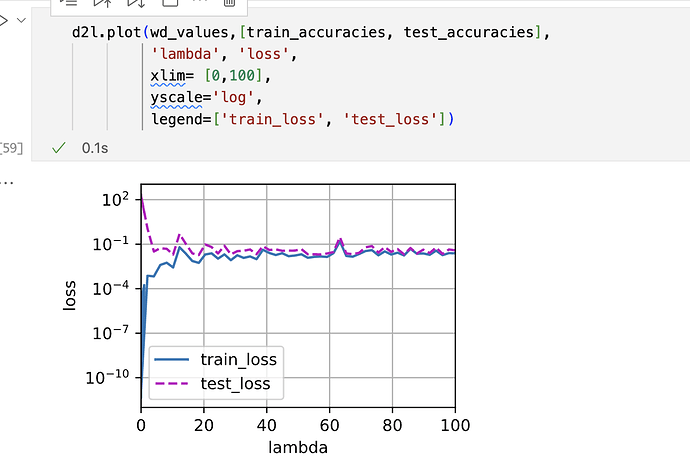
实验从1到50,lambda很小的时候,训练误差也小,但是测试误差大,随着增大,到10左右到达一个两者都较小的时候,随后lambda继续增加,这两个指标在不断震荡
编辑器不是一开始书中就有交代么,Jupyter 记事本
对于第一问,我的代码如下:
def train_concise(wd):
net = nn.Sequential(nn.Linear(num_inputs, 1))
for param in net.parameters():
param.data.normal_()
loss = nn.MSELoss(reduction=‘none’)
num_epochs, lr = 100, 0.003
# 偏置参数没有衰减
trainer = torch.optim.SGD([
{“params”:net[0].weight,‘weight_decay’: wd},
{“params”:net[0].bias}
], lr=lr)
‘’’
animator = d2l.Animator(xlabel=‘epochs’, ylabel=‘loss’, yscale=‘log’,
xlim=[5, num_epochs], legend=[‘train’, ‘test’])
‘’’
for epoch in range(num_epochs):
for X, y in train_iter:
trainer.zero_grad()
l = loss(net(X), y)
l.mean().backward()
trainer.step()
‘’’
if (epoch + 1) % 5 == 0:
animator.add(epoch + 1,
(d2l.evaluate_loss(net, train_iter, loss),
d2l.evaluate_loss(net, test_iter, loss)))
‘’’
print(‘w的L2范数:’, net[0].weight.norm().item())
return net, loss
lambd_data = np.arange(0, 101, 2)
animator = d2l.Animator(xlabel=‘lambd’, ylabel=‘loss’, yscale=‘log’,
xlim=[0, 100], legend=[‘train’, ‘test’])
for lambd in lambd_data:
# print(lambd)
net, loss = train_concise(lambd)
animator.add(
lambd,
(
d2l.evaluate_loss(net, train_iter, loss),
d2l.evaluate_loss(net, test_iter, loss)
)
)
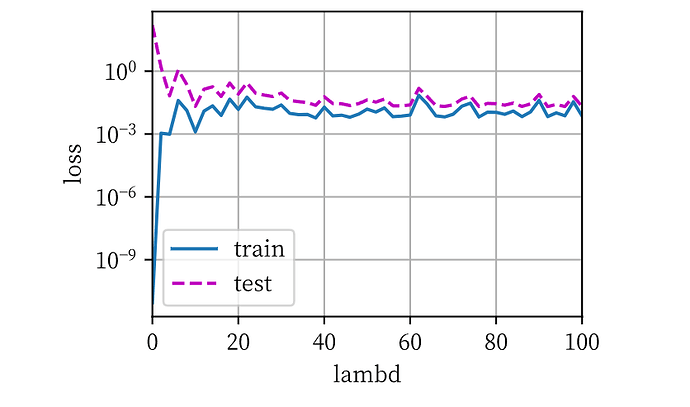
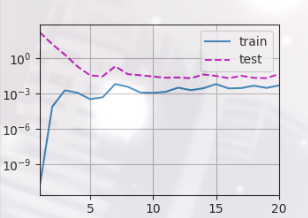
实验结果如下:
lambd到了40之后,test loss就不再有明显的变化
分享一个自己的小疑问:为什么在3.2;3.3;4.5这三个小节求导backward()之前对损失l进行了不同的操作:l.backward() or l.mean().backward() or l.sum().backward()?
首先,nn.MSELoss()函数中有一个参数'reduction',reduction=’none’,则返回的是tensor:
loss1 = nn.MSELoss(reduction='none')
input = torch.randn(3, 5, requires_grad=True)
target = torch.randn(3, 5)
output = loss1(input, target)
print(output)
>>>tensor([[0.8527, 3.0810, 0.1368, 0.7540, 0.2062],
[0.3132, 0.1920, 0.0260, 4.0326, 1.9805],
[0.8947, 1.0306, 5.3231, 0.5385, 0.3706]], grad_fn=<MseLossBackward0>)
不设置reduction,则返回的是均值:
loss1 = nn.MSELoss()
input = torch.randn(3, 5, requires_grad=True)
target = torch.randn(3, 5)
output = loss1(input, target)
print(output)
>>>tensor(1.6413, grad_fn=<MseLossBackward0>)
而在线性回归中,小批量梯度下降需要满足:
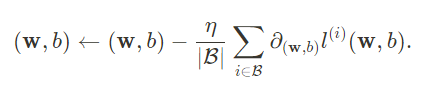
即优化器中,减掉的梯度向量一定是小批量中每个样本梯度的均值。所以,在3.2;3.3;4.5这三节中,对应的代码表达的意思是一致的:
3.2:
sgd()函数是自己定义的,在sgd()内部实现了求梯度对batchsize的均值
def sgd(params, lr, batch_size): #@save
"""小批量随机梯度下降"""
with torch.no_grad():
for param in params:
param -= lr * param.grad / batch_size
param.grad.zero_()
lr = 0.03
num_epochs = 3
net = linreg
loss = squared_loss
for epoch in range(num_epochs):
for X, y in data_iter(batch_size, features, labels):
l = loss(net(X, w, b), y) # X和y的小批量损失
# 因为l形状是(batch_size,1),而不是一个标量。l中的所有元素被加到一起,
# 并以此计算关于[w,b]的梯度
l.sum().backward()
sgd([w, b], lr, batch_size) # 使用参数的梯度更新参数
with torch.no_grad():
train_l = loss(net(features, w, b), labels)
print(f'epoch {epoch + 1}, loss {float(train_l.mean()):f}')
3.3:
使用torch的SGD()和MSELoss(),这里的MSELoss()没有参数,因此默认求batchsize的均值。所以下面直接用l.backward()
**loss = nn.MSELoss()**
**trainer = torch.optim.SGD(net.parameters(), lr=0.03)**
num_epochs = 3
for epoch in range(num_epochs):
for X, y in data_iter:
l = loss(net(X) ,y)
trainer.zero_grad()
l.backward()
trainer.step()
l = loss(net(features), labels)
print(f'epoch {epoch + 1}, loss {l:f}')```
4.5:
MSELoss()有参数reduction='none',因此返回的是tensor,所以需要对loss求均值,用l.mean().backward()
def train_concise(wd):
net = nn.Sequential(nn.Linear(num_inputs, 1))
for param in net.parameters():
param.data.normal_()
loss = nn.MSELoss(reduction='none')
num_epochs, lr = 100, 0.003
# 偏置参数没有衰减
trainer = torch.optim.SGD([
{"params":net[0].weight,'weight_decay': wd},
{"params":net[0].bias}], lr=lr)
animator = d2l.Animator(xlabel='epochs', ylabel='loss', yscale='log',
xlim=[5, num_epochs], legend=['train', 'test'])
for epoch in range(num_epochs):
for X, y in train_iter:
trainer.zero_grad()
l = loss(net(X), y)
l.mean().backward()
trainer.step()
if (epoch + 1) % 5 == 0:
animator.add(epoch + 1,
(d2l.evaluate_loss(net, train_iter, loss),
d2l.evaluate_loss(net, test_iter, loss)))
print('w的L2范数:', net[0].weight.norm().item())
FYI.
def train_concise(wd):
net = nn.Sequential(nn.Linear(num_inputs, 1))
for param in net.parameters():
param.data.normal_()
loss = nn.MSELoss(reduction=‘none’)
num_epochs, lr = 100, 0.003
# 偏置参数没有衰减
trainer = torch.optim.SGD([
{“params”:net[0].weight,‘weight_decay’: wd},
{“params”:net[0].bias}], lr=lr)for epoch in range(num_epochs): for X, y in train_iter: trainer.zero_grad() l = loss(net(X), y) l.mean().backward() trainer.step() return net print('w的L2范数:', net[0].weight.norm().item())animator = d2l.Animator(xlabel=‘lambda’, ylabel=‘loss’, yscale=‘log’,
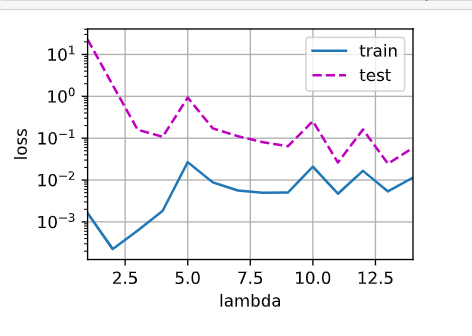
xlim=[1, 14], legend=[‘train’, ‘test’])
loss = nn.MSELoss(reduction=‘none’)
for i in[1,2,3,4,5,6,7,8,9,10,11,12,13,14]:net=train_concise(i) animator.add(i, (d2l.evaluate_loss(net, train_iter, loss), d2l.evaluate_loss(net, test_iter, loss)))
# 简洁实现
def train(wd):
net = nn.Sequential(nn.Linear(num_inputs, 1)) # 定义网络
for param in net.parameters():
param.data.normal_() # 初始化参数
loss = nn.MSELoss(reduction='none') # 损失
num_epochs, lr = 100, 0.003
# 设置参数衰减
trainer = torch.optim.SGD([
{'params':net[0].weight, 'weight_decay':wd},
{'params':net[0].bias}], lr=lr)
for epoch in range(num_epochs):
for X, y in train_iter:
trainer.zero_grad()
l = loss(net(X), y)
l.mean().backward()
trainer.step()
return d2l.evaluate_loss(net, train_iter, loss), d2l.evaluate_loss(net, test_iter, loss)
# print('w的L2范数:', net[0].weight.norm().item())
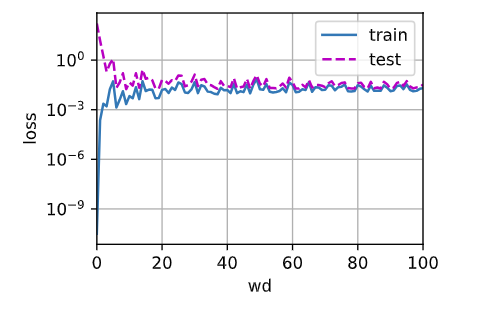
max_wd = 100
animator = d2l.Animator(xlabel='wd', ylabel='loss', yscale='log', xlim=[0, max_wd], legend=['train', 'test'])
for wd in range(max_wd+1):
l_train, l_test = train(wd)
animator.add(wd, (l_train, l_test))
argmaxP(x | w)P(w) = argmin -lnP(xi | w) - lnP(w)是怎么得来的