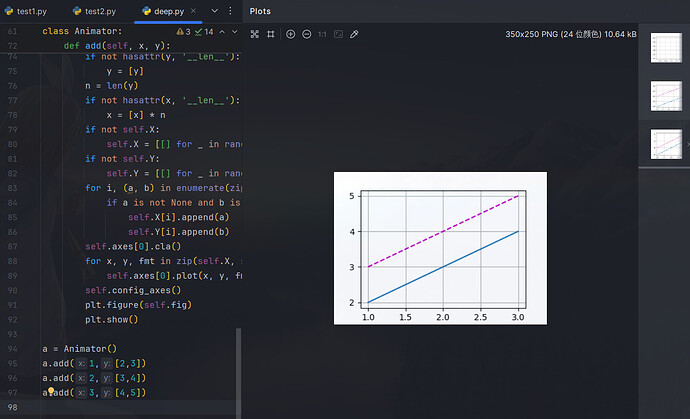
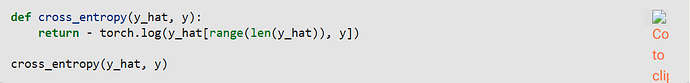如果使用pycharm的话,需要调用d2l.plt.show()来显示图像,但是默认主程序和显示图像的程序共用一个线程,如果调用d2l.plt.show()显示图像的话,主程序就会一直等待直到关闭图像窗口而不会继续运行训练函数。所以如果想实现图像随训练结果更新而更新的话需要自己创建多个线程,一个用来显示图像,一个用来跑训练函数。我认为如果不纠结实现图像实时更新的效果的话,可以在train_ch3函数的最后添加d2l.plt.show(),即显示最终绘制的图像,来观察效果即可(图像会在跑完10个epoch后才会出现,需要等待训练函数跑完)。
accuracy方法中的y_hat.argmax(axis=1),这个argmax方法没有axis参数和可变参数,应该改为y_hat.argmax(dim=1)。
只需要把add()方法末尾那两句改成
# 删除
display.display(self.fig)
display.clear_output(wait=True)
# 添加
plt.figure(self.fig)
plt.show()
这样每次调用add的时候都会显示这个时候的数据图。
调用了三次add方法,输出每次的图片。
本节直接实现了基于数学定义softmax运算的softmax函数。这可能会导致什么问题?
在 Python 中 float 类型基于 C 语言中的 double 类型。我们定义的softmax函数由于分母和分子中都存在指数函数,因此有可能计算过程中会产生过于巨大的数加和的情况,从而导致溢出和无法求解。
本节中的函数cross_entropy是根据交叉熵损失函数的定义实现的。它可能有什么问题?
交叉熵损失包含对概率的对数操作。如果输入接近 0 或 1,直接取对数会导致数值不稳定(趋向于负无穷或正无穷)。
请想一个解决方案来解决上述两个问题
softmax中可以在指数中减去最大数,这样能保证一般情况下不会有特别大的数字。交叉熵则是设定一个0-1的子区间,防止溢出。
返回概率最大的分类标签总是最优解吗?例如,医疗诊断场景下可以这样做吗?
不一定,因为模型本身训练效果就是不保证准确的,可以按照各自的最终数值概率选取一个标签。我认为医疗情境下不可以这么做,因为医疗情景需要排除大概率患病可能,因此输出概率前几的病症更符合实际需求。
假设我们使用softmax回归来预测下一个单词,可选取的单词数目过多可能会带来哪些问题?
不可避免的导致训练效果很差,因为概率总和为1,那么数目特别多就意味着很多单词几乎都是零概率,白白浪费了计算资源。
这个是说你这个jupyter notebook所在的文件夹的上一级文件夹里要有个data文件夹,然后数据会下载到那里,但是你没有权限在新建data文件夹或者操作这个文件夹,可以把…/data改成./data,也就是jupyter notebook所在的文件夹里直接建一个data文件夹
为什么我从d2l.torch导入不了 train_epoch_ch3以及一些其他已经saved的包
AttributeError: module ‘d2l.torch’ has no attribute ‘train_epoch_ch3’. Did you mean: ‘train_batch_ch13’?
我在d2l.torch文件离可以看到这些函数,但是却导入不了
我也遇到了一样的问题,请问你知道如何解决了吗
将过程代码改为了类版本,针对此章节精简了一些暂不必要的代码,如去除标准模型和优化器的检测代码,专注于“从零实现”,另外 Accumulator 和 Animator 类没改,直接使用,
希望对大家的理解有帮助,有问题一起交流,共同进步!
import torch
from IPython import display
from d2l import torch as d2l
class Trainer:
def __init__(
self,
num_inputs=784,
num_outputs=10,
lr:float=0.1, # 学习率
num_epochs:int=10, # 迭代次数
train_iter=None,
test_iter=None
):
self.num_inputs = num_inputs
self.num_outputs = num_outputs
self.lr = lr
self.num_epochs = num_epochs
self.train_iter = train_iter
self.test_iter = test_iter
self.W = torch.normal(0, 0.01, size=(self.num_inputs, self.num_outputs), requires_grad=True)
self.b = torch.zeros(self.num_outputs, requires_grad=True)
pass
def _softmax(self, X):
'''输出层softmax'''
X_exp = torch.exp(X)
partition = X_exp.sum(1, keepdim=True)
return X_exp / partition # 这里应用了广播机制
def _net(self, X):
'''模型'''
return self._softmax(torch.matmul(X.reshape((-1, self.W.shape[0])), self.W) + self.b)
def _loss(self, y_hat, y):
'''cross_entropy'''
return - torch.log(y_hat[range(len(y_hat)), y])
def _accuracy(self, y_hat, y): #@save
"""计算预测正确的数量(单批精度)"""
if len(y_hat.shape) > 1 and y_hat.shape[1] > 1:
y_hat = y_hat.argmax(axis=1)
cmp = y_hat.type(y.dtype) == y
return float(cmp.type(y.dtype).sum())
def _evaluate_accuracy(self, data_iter): #@save
"""计算在指定数据集上模型的精度"""
metric = Accumulator(2) # 正确预测数、预测总数
with torch.no_grad():
for X, y in data_iter:
metric.add(self._accuracy(self._net(X), y), y.numel())
return metric[0] / metric[1]
def _updater(self, batch_size):
'''优化器'''
return d2l.sgd([self.W, self.b], self.lr, batch_size)
def _epoch(self, data_iter): #@save
"""单个训练周期: 训练模型一个迭代周期(定义见第3章)"""
# 训练损失总和、训练准确度总和、样本数
metric = Accumulator(3)
for X, y in data_iter:
y_hat = self._net(X)
l = self._loss(y_hat, y)
# 定制的优化器和损失函数
l.sum().backward()
# 更新参数
self._updater(X.shape[0])
# 累加器累加损失、准确度和样本数
metric.add(float(l.sum()), self._accuracy(y_hat, y), y.numel())
# 返回训练损失和训练精度
return metric[0] / metric[2], metric[1] / metric[2]
def epochs(self, train_iter, test_iter, num_epochs): #@save
"""训练模型(定义见第3章)"""
animator = Animator(xlabel='epoch', xlim=[1, num_epochs], ylim=[0.3, 0.9],
legend=['train loss', 'train acc', 'test acc'], figsize=(7, 5))
for epoch in range(num_epochs):
train_metrics = self._epoch(train_iter)
test_acc = self._evaluate_accuracy(test_iter)
animator.add(epoch + 1, train_metrics + (test_acc,))
train_loss, train_acc = train_metrics
assert train_loss < 0.5, train_loss
assert train_acc <= 1 and train_acc > 0.7, train_acc
assert test_acc <= 1 and test_acc > 0.7, test_acc
def run(self):
'''训练'''
self.epochs(self.train_iter, self.test_iter, self.num_epochs)
def predict(self, data_iter, n=6):
"""预测标签(定义见第3章)"""
for X, y in data_iter:
break
trues = d2l.get_fashion_mnist_labels(y)
preds = d2l.get_fashion_mnist_labels(self._net(X).argmax(axis=1))
titles = [true +'\n' + pred for true, pred in zip(trues, preds)]
d2l.show_images(
X[0:n].reshape((n, 28, 28)), 1, n, titles=titles[0:n])
# 训练
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size=256)
trainer = Trainer(train_iter=train_iter, test_iter=test_iter)
trainer.run()
# 预测
trainer.predict(test_iter, 10)
版本问题:打开你本地的jupyter notebook,找到安装,然后找到pip install d2l=xxxxx
不建议改源码,试试这个:不建议改源码,试试这个:
@d2l.add_to_class(d2l.FashionMNIST)
def set_num_workers(self, num=4):
self.num_workers = num
data = d2l.FashionMNIST(batch_size=256)
data.set_num_workers(0)
3.6.9 练习
第三题解决方案:可以在forward的过程中不要拆开softmax层和loss层的计算,而是把二者合并。
根据3.4.6.2. softmax及其导数中提到的softmax和交叉熵组合的计算公式,拆开算容易遇到溢出问题在组合公式中解决了:如果o_k太大,那log就会压低它的值;而exp(o_k)又使得log不太可能得到接近0的值。
import os
import requests
import gzip
import shutil
import time
base_url = "http://fashion-mnist.s3-website.eu-central-1.amazonaws.com/"
files = [
"train-images-idx3-ubyte.gz",
"train-labels-idx1-ubyte.gz",
"t10k-images-idx3-ubyte.gz",
"t10k-labels-idx1-ubyte.gz"
]
save_dir = os.path.expanduser("~/data/FashionMNIST/raw")
os.makedirs(save_dir, exist_ok=True)
def download_with_resume(url, save_path):
temp_path = save_path + ".part"
headers = {}
while True:
try:
# 已下载大小
downloaded_size = 0
if os.path.exists(temp_path):
downloaded_size = os.path.getsize(temp_path)
headers['Range'] = f'bytes={downloaded_size}-'
print(f"检测到已有部分文件,尝试断点续传,从 {downloaded_size} 字节开始下载...")
else:
print("开始下载新文件...")
with requests.get(url, headers=headers, stream=True, timeout=10) as r:
r.raise_for_status()
# 如果响应状态码是206,表示支持断点续传
mode = 'ab' if r.status_code == 206 else 'wb'
with open(temp_path, mode) as f:
for chunk in r.iter_content(chunk_size=8192):
if chunk:
f.write(chunk)
downloaded_size += len(chunk)
print(f"\r已下载 {downloaded_size} 字节", end='', flush=True)
print("\n下载完成,准备重命名文件...")
os.rename(temp_path, save_path)
return
except requests.exceptions.RequestException as e:
print(f"\n下载出现错误:{e},5秒后重试...")
time.sleep(5)
def download_and_extract(filename):
url = base_url + filename
save_path = os.path.join(save_dir, filename)
download_with_resume(url, save_path)
# 解压 .gz 文件
with gzip.open(save_path, 'rb') as f_in:
with open(save_path.replace(".gz", ""), 'wb') as f_out:
shutil.copyfileobj(f_in, f_out)
print(f"完成: {filename}")
for f in files:
download_and_extract(f)
print(" FashionMNIST 数据下载并解压完成!")
在下载代码前使用这一段代码来下载
我的理解时这里y的值是将独热向量中为1 的值的索引值拿出来放着这里y=[0,2]表示 第一个样本中真实类别的索引值为0,第二个样本中真实的索引值为2
所以在预测值里y_hat=torch.tensor([0.1,0.3,0.6],[0.3,0.2,0.5])
y_hat[[0,1],y] #这个代码的意思 y_hat[[0,1],[0,2]] 第一个 [0,1] 表示的时样本,[0,2]表示的时 真实类别对应的索引
那么输出值 为 0.1 0.5
0.1 表示 第一个样本中 真实类别 对应的预测概率
0.5 表示 第二个样本中 真实类别 对应的预测概率
也就是说 比如小猫,小狗 两个类别
样本1 的真实类别是 小狗 0.1 就对应经过softmax函数 预测 样本1 为小狗的概率
样本2 的真实类别是 小猫 0.5 就对应 经过softmax函数预测样本2 为小猫的概率
所以在后面的 交叉熵函数的代码中 直接 输出的是 log(预测概率值) 因为 独热向量【0,1】 中0 的结果=0 所以这里省略的每个都乘一次的步骤,直接就是 log(1* 概率)=log(概率)
事实上,取前取后对总体Loss影响并不大,我们要的主要还是一个趋势,但是用本次因为当时前向传播已经算过一次,直接用整体效率会更高些