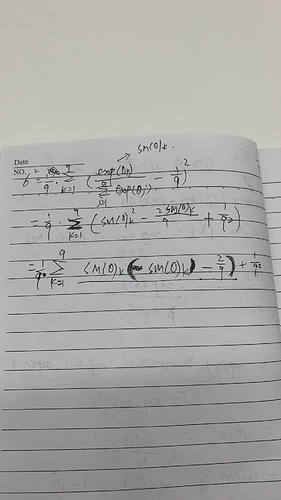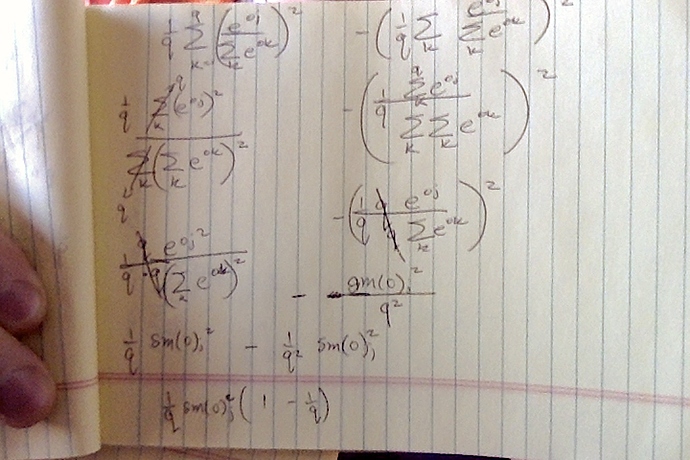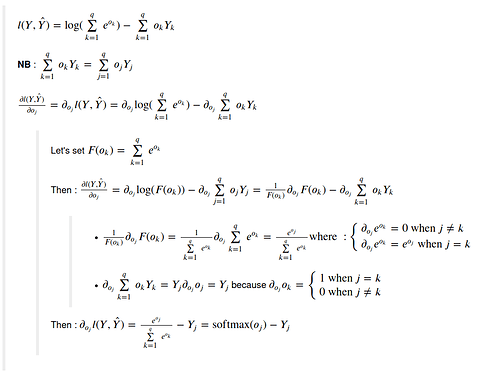Softmax Regression

[StevenJokes]

The green thing is same.

[Abinash_Sahu]

Thank you for your response. My question was more specifically why
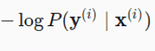is same as
l(y,y_hat)

Is this because y when 1-hot encoded has only single position with 1 and hence when we sum up the y * log(y_hat) over the entire class, we are left with the probability y_hat corresponding to true y. Please advise.

[StevenJokes]

@Abinash_Sahu

Is this because y when 1-hot encoded has only single position with 1 and hence when we sum up the y * log(y_hat) over the entire class, we are left with the probability y_hat corresponding to true y. Please advise.

@Abinash_Sahu
l (y，y _ hat)

Cross entropy loss
Only one type of these losses we often use.
https://ml-cheatsheet.readthedocs.io/en/latest/loss_functions.html

---

[JMianT]

Q1.2. Compute the variance of the distribution given by softmax(𝐨)softmax(o) and show that it matches the second derivative computed above.

Can someone point me in the right direction? I tried to use Var[𝑋]=𝐸[(𝑋−𝐸[𝑋])^2]=𝐸[𝑋^2]−𝐸[𝑋]^2 to find the variance but I ended up having the term 1/q^2… it doesn’t look like the second derivative from Q1.1.

Thanks!

[Premkumar_Devanbu]

It appears that there is a reference that remained unresolved:
:eqref: eq_l_cross_entropy

in 3.4.5.3

[astonzhang]

Thanks. Now it’s fixed. See comments in https://github.com/d2l-ai/d2l-en/issues/1448

[JH.Lam]

to keep unified form,should the yj in later two equations should have an upper right mark (i) ?

[JH.Lam]

me too. is there sth wrong?

[learner]

I cannot understand the equation in 3.4.9

[FBT]

@Abinash_Sahu, @StevenJokess

I may have an explanation considering equivalence between log likehood and cross-entropy.

[six]

Looks like you have der(E[X]^2), but what about E[X^2]? Recall:
Var[X] = E[X^2] - E[X]^2

[six]

From steps 2->3 and 3->4, does Sum_k_to_q actually resolve to q?

[six]

3.1 is strait forward to show.

I’m having trouble with 3.2 and 3.3:

3.2:

Show:
   ⎛   a      b⎞
log⎝𝜆⋅ℯ  + 𝜆⋅ℯ ⎠
──────────────── > Max(a, b)
       𝜆

Assume:
    a > b
    𝜆 > 0

(Max(a,b) -> a, b/c a > b)

   ⎛   a      b⎞
log⎝𝜆⋅ℯ  + 𝜆⋅ℯ ⎠
──────────────── > a
       𝜆

   ⎛   a      b⎞
log⎝𝜆⋅ℯ  + 𝜆⋅ℯ ⎠ > 𝜆a

(exp both sides)

   a      b    𝜆a
𝜆⋅ℯ  + 𝜆⋅ℯ  > ℯ

LHS !> RHS

and 3.3:
I did the calculus and the limit looked like it was going to zero (instead of max(a,b)) so I coded up the function in numpy to check, and indeed it appears to go to 0 instead of 4 in this case (a=2, b=4).

[nav] In [478]: real_softmax = lambda x: 1/x * np.log(x*np.exp(2) + x*np.exp(4))

[ins] In [479]: real_softmax(.1)
Out[479]: 18.24342918048927

[nav] In [480]: real_softmax(1)
Out[480]: 4.126928011042972

[ins] In [481]: real_softmax(10)
Out[481]: 0.6429513104037019

[ins] In [482]: real_softmax(1000)
Out[482]: 0.01103468329002511

[ins] In [483]: real_softmax(100000)
Out[483]: 0.000156398534760132

Please advise

[JH.Lam]

thanks.but i use the definition of variance to derive while your advice is to use inference of variance to do that.both are same in fact

[JH.Lam]

i think you have a mistake at the usage of ∑a/b != ∑a/∑b but ∑a / b as the denominator is public

[Reno]

Hi,
1.1 see 1.2
1.2
import numpy as np

output = np.random.normal(size = (10, 1))

def softmax(output):
denominator = sum(np.exp(output))
return np.exp(output)/denominator

st = softmax(output)
st_2nd = st - st**2

np.var(st)
np.var(st_2nd)

3.1 very simple to prove, just move a or b to left, we prove no matter which one moves to left, we can get [exp(a) + exp(b)]/exp(a) or [exp(a) + exp(b)]/exp(b) and both are greater than 1 so we can prove softmax is larger.

[fabipy]

Hi,

I’m struggling with how the Softmax formula 3.4.9 is re-written (after plugging it in into the loss fct)

I think I understand the first part as you can see from my notes:
https://i.imgur.com/qOq0uuz_d.webp?maxwidth=760&fidelity=grand

However, I struggle to make sense of the lines that come after.

Is the result of 3.4.9 already the derivative, or is it only re-written? And how do they get from 3.4.9 to 3.4.10?

I’m still at the beginning of my DL journey and probably need to freshen up my calculus as well. If someone could point out to me how the formula is transformed that would be great!! I’ve been trying for a while now to write it out, but can’t seem to figure out how it should be done.

this is a great explanation of how the softmax derivative (+ backprop) works which I could follow and understand. But I have problems connecting the solution back to the (more general) formula in 3.4.9

Some help would be much appreciated!

[fabipy]

I have the same issue!!
Have you figured it out?

[fabipy]

I think I figured it out.
For anyone who is stuck, maybe this helps: My notes

[FBT]

Is the result of 3.4.9 already the derivative, or is it only re-written?

3.4.9 is only the rewritten expression of lost function, not the derivative. It comes mostly from the fact log(a/b) = log(a)-log(b) and that log(exp(X)) = X

And how do they get from 3.4.9 to 3.4.10?

Please check path on the picture here-under