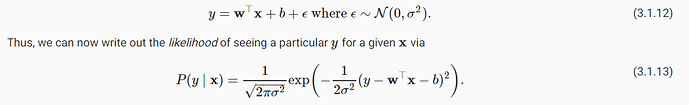https://d2l.ai/chapter_linear-regression/linear-regression.html
i believe, for linear regression the assumption is that the residuals has to be normally distributed the noise ‘e’ y=w⊤x+b+ϵ where ϵ∼N(0,σ2) need not be
May I ask a question related to the normalization:
For categorical variable, once convert it to dummy variables (via 1-Hot encoding), is it worth to do standard normalization for it? Or what scenarios it is worth doing and what scenarios it may not?
Thanks in advance!
Hi @Angryrou, can you elaborate more on normalization. I imagine you mean normalizing the numerical features to a normal distribution? Or you mean Batch Normalization?
Sorry for the ambiguous. I mean normalizing the numerical features to a normal distribution. E.g., using sklearn.preprocessing.MinMaxScaler / StandardScaler.
Take preprocessing features like (age, major, sex, height, weights) for a students as a more concrete example. After fill null values and convert categorical variables to dummy vectors, I would like to do normalization for all the features. For the dummy vectors from categorical variables, is it worth to do standard normalization for it? Or what scenarios it is worth doing and what scenarios it may not?
Hey @Angryrou, you are right about normalization! And it is extremely important in deep learning world. For the numerical feature, we just apply normalization on the scalar values. While for the categorical feature, we represent its scalar value as a vector (via one-hot encoding). The feature will be look like a list of zeros and ones, and we don’t normalize further beyond that.
We combine those normalized scalar features (from numerical features) and one-hot vectors (from categorical features) together, and feed the combinations to the neural nets.
How did we arrive at the equation - likelihood of seeing a particular y for a given x (equation 3.1.13 )
Could someone explain ? Thanks
Hey @rammy_vadlamudi, I derived equation 3.1.13 by following the log rules.
By taking the log of a product of many terms, that turned into a sum of the logs of those terms, so negative log of likelihood = - sum(log(p(y(i)|x(i))))
log(p(y(i)|x(i))) can be similarly expanded into log(1/sqrt(…)) + log(e(…)), which simplifies further. Keep in mind that sqrt is the same as a 1/2 power, and you can apply another log rule there. I was able to successfully derive that equation by applying the various log rules a few times.
Good luck! 
I am referring to equation 3.1.13
The part where (y-wTx-b)**2 is used in place of (x-mean)**2
@leifan89 Thanks 
@rammy_vadlamudi Ah! My apologies, I had misread your question 
I’m not 100% sure on that derivation. My take on the derivation is that, if epsilon ~ N(0, sigma2), and epsilon = y - wTx - b, then (y - wTx -b) ~ N(0, sigma2). Since epsilon is the random variable here and x is given, the distribution of y is a linear transformation of the distribution of epsilon. With a mean of 0, I simply substitute epsilon as a function of y and x into the place of the random variable. So, to me, I took P(y|x) to actually mean P(y|x,e).
But, like I said, I’m not 100% if that’s a strictly correct reasoning mathematically (in fact, I feel like I’ve skipped some steps here, or completely went down the wrong path). I’d love to see if anyone else has a definitive answer? 
Just a side note: The likelihood is a function of the parameters, here w and b., see e.g. David MacKay’ s book (https://www.inference.org.uk/itprnn/book.pdf p. 29):
“Never say ‘the likelihood of the data’. Always say ‘the likelihood of the parameters’. The likelihood function is not a probability distribution.”
This is not completely clear in the description.
hello ,
thanks for your effort here in such book ,
i would like to know , if i can find the answers for the exercises?
thanks again
Hi @alaa-shubbak, thanks for your engagement! We are focusing on improving the content of current chapter and looking for community contributors for the solutions.
hi @goldpiggy may i know how to evaluate analytical solution
Can u help by solving the first qn
thanks
Hi.
In chapter 3.1.1.3 we got the analytical solution by this formula:
w∗=(X⊤X)−1X⊤y
by that, we have a hidden assumption that X⊤X is reversible matrix.
how can we assume that?
thanx a lot.
If anyone knows the answer of Q3 of exercise, I will be more than happy if you comment me 
My current answer:
- neg-likelihood: sum(on i from 1 to n) of |y_i - x_i’w|
- I have no idea how to obtain the gradient of sum of absolute values.
- Since the target function is the sum of absolute values of linear combinations of w, the gradient of w, no matter how complicated it can be, must be piecewise constant. Which means, the gradient can never converge to 0, which means there is no STOP of updating w.
How to fix: I have no good idea. Maybe we have to make the learning rate converge to 0 during learning.
when we regard x as random variable and w, b as known parameters, then that’s the density function. We all know that.
But then the x are sampled and known, but parameters w, b are unknown, on this condition the same formula becomes the “likelihood function”. So we don’t derive likelihood, we just rename the density as likelihood(However the situation is different).
This is my answers for Q3.
- Assume that y=Xw+b+ϵ,p(ϵ)=1/2e^(−|ϵ|)=1/2e^(−|y−y^|) . So , P(y|x)=1/2e^(−|y−y^|) .
Negative log-likelihood: LL(y|x)=−log(P(y|x))=−log(∏p(y(i)|x(i)))=∑log2+|y(i)−y^(i)|=∑log2+|y(i)−X(i)w−b| - ∇{w} LL(y|x)=X.T*(Xw−y/|Xw−y|)=0 . From the equation, we get that: (1) : w=(X.T X)^−1 X.T y and (2) w≠X^−1 y
About Q3.3, I am confused about loss function.
First, please confirm my opinion that determining loss function might affect to the prior assumption of Linear regression model, specially noise distribution and vice versa. In the book, there is a sentence “It follows that minimizing the mean squared error(MSE) is equivalent to maximum likelihood estimation of a linear model under the assumption of additive Gaussian noise.” So what if linear model do not follow Gaussian noise but other noises, can we use MSE (y-y_hat)^2 for loss function again? Or use principle of maximum likelihood( which lead to another loss function ,i.e |y-y_hat|).
Second, how can we determine loss function if we don’t know about noise distribution in practical data? I think we may use some normality test to test the normality of data, but what if the data do not follow Gaussian distribution but p(ϵ) = 1/2*e^(−|ϵ|) for example?
Thanks a lot
“3.1.2 Vectorization for Speed
When training our models, we typically want to process whole minibatches of examples simulta-
neously.”
From my understanding, the above statement should have “minibatch” rather than “minibatches”…
Thank you
Nisar
The section 3.1.3 is a bit difficult to understand. I have 2 questions:
i) In formula 3.1.13, Why P(y|x) equals to P(ϵ) ?
ii) And does ϵ equals to y minus y_cap ?
Thanks a lot!