Linear Algebra

[StevenJokes]

@manuel-arno-korfmann

the matrix

@manuel-arno-korfmann
I think @goldpiggy is right.
A_mn:

AT_nm:

[Fillipe_Santos]

Its said that “By default, invoking the function for calculating the sum reduces a tensor along all its axes to a scalar. We can also specify the axes along which the tensor is reduced via summation. Take matrices as an example. To reduce the row dimension (axis 0) by summing up elements of all the rows, we specify axis=0 when invoking the function.” Are you sure? Look at my code:

A = torch.arange(25).reshape(5,5)

A, A.sum(axis = 1)

(tensor([[ 0, 1, 2, 3, 4],
[ 5, 6, 7, 8, 9],
[10, 11, 12, 13, 14],
[15, 16, 17, 18, 19],
[20, 21, 22, 23, 24]]),
tensor([ 10, 35, 60, 85, 110]))

When axis = 1, all elements in row 0 are added.
Otherwse (axis = 0), all elements colummns are added.

I didn’t understand that. Could you explain it with more details, please?

[rahulvigneswaran]

Maybe this reply is too late but here you go.

Your understanding of row vs column is wrong.

In,

tensor([[ 0, 1, 2, 3, 4],
[ 5, 6, 7, 8, 9],
[10, 11, 12, 13, 14],
[15, 16, 17, 18, 19],
[20, 21, 22, 23, 24]])

[ 0, 1, 2, 3, 4] is a column and [ 0, 5, 10, 15, 20] is a row.

[rahulvigneswaran]

It feels like the following solution is more appropriate for question 6 as there is no change in the actual value of A like in your answer.

A = torch.arange(20, dtype = torch.float32).reshape(5, 4)

A / A.sum(axis=1, keep_dim=True)

After using keep_dim=True, broadcasting happens and dimensionality error would disapper.

[dhern023]

Your understanding of row vs column is wrong.

Are you sure you don’t have it backwards?

A = torch.arange(25, dtype = torch.float32).reshape(5,  5)

"""
>>> A
tensor([[ 0.,  1.,  2.,  3.,  4.],
        [ 5.,  6.,  7.,  8.,  9.],
        [10., 11., 12., 13., 14.],
        [15., 16., 17., 18., 19.],
        [20., 21., 22., 23., 24.]])

>>> A[0] 
tensor([0., 1., 2., 3., 4.])

>>> A[:,0] # Fix column 0, run across rows
tensor([ 0.,  5., 10., 15., 20.])

>>> A[0, :] # Fix row 0, run across columns
tensor([0., 1., 2., 3., 4.])
"""

[CannedWalk]

About the exercises, the questions needed to be coded or mathematically solved?

[object_tracking]

Can anybody solve the No. 9 in the exercise.

[Sameer_Kumar]

Hi, I gave it a shot and here is what I found:

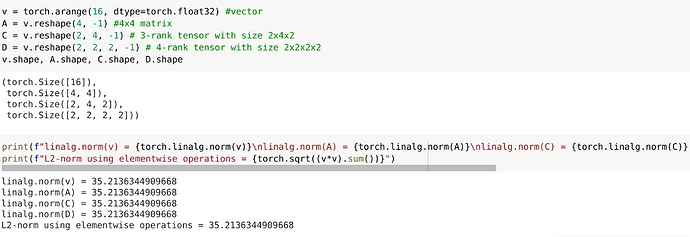
The torch.linalg.norm function computes the L2-norm no matter the rank of a Tensor. In other words, it squares all the elements of a Tensor, sums them up, and reports the square root of the sum.

I hope this helps. Thanks.

[GpuTooExpensive]

About Exersize.11
After some testing, I think using C=B^T is fater

Here is the code for testing:

import torch
import time

a = torch.randn([2**10,2**16])
b = torch.randn([2**16,2**5])
c = torch.randn([2**5,2**16])
start = time.time()
a@b
end = time.time()
delay0 = end-start
start = time.time()
a@c.T
end = time.time()
delay1 = end-start
print(delay0, ',', delay1, '|', delay0/delay1)

d = torch.randn([2**10,2**16])
e = torch.randn([2**16,2**5])
f = e.T
start = time.time()
d@e
end = time.time()
delay0 = end-start
start = time.time()
d@f.T
end = time.time()
delay1 = end-start
print(delay0, ',', delay1, '|', delay0/delay1) 

The outputs in jupyter are:
the first time:
0.09555768966674805 , 0.07239270210266113 | 1.3199906467261895
0.07950305938720703 , 0.08091998100280762 | 0.9824898424586701
the second time
0.08409309387207031 , 0.06908702850341797 | 1.2172052510249438
0.07972121238708496 , 0.07754659652709961 | 1.028042698936831

I test it for several times, the results are likely, but I’m not so sure , because the difference between them is not so obvious, so is there anybody who have any other way to do this exercise?

Note: my memory of computer is 8GB, memory of GPU is 4GB, I tried the matrices below to reach the memory limit and then my jupyter kernel went died and forced to restarted…

a = torch.randn([2**10,2**21])
b = torch.randn([2**21,2**5])
c = torch.randn([2**5,2**21])

[Tejas-Garhewal]

My attempts :

Exercises

1. Prove that the transpose of the transpose of a matrix is the matrix itself: $ (\mathbf{A}^\top)^\top = \mathbf{A} $

The $ (i, j)^{th} $ element of A corresponds to $ (j, i)^{th} $ element of $ \mathbf{A}^{\top} $, so the $ (i, j)th $ element of $ (\mathbf{A}^{\top})^{\top} $ will correspond to the $ (j, i)^{th} $ element of $ \mathbf{A}^{\top} $, which corresponds to the $ (i, j)^{th} $ element of $ \mathbf{A} $; therefore the two will be equal

2. Given two matrices $ mathbf{A} $ and $ mathbf{B} $, show that sum and transposition commute: $ \mathbf{A}^\top + \mathbf{B}^\top = (\mathbf{A} + \mathbf{B})^\top $.

$ (j, i)^{th} $ element of $ \mathbf{A}^\top $ + $ (j, i)^{th} $ element of $ \mathbf{B}^\top $ are equal to the $ ( \mathbf{i}, \mathbf{j})^{th} $ element of $ \mathbf{A} + \mathbf{B} $, therefore the two will be equal if we transpose $ \mathbf{A} + \mathbf{B} $

3. Given any square matrix $ \mathbf{A} $ , is $ \mathbf{A} $ + $ \mathbf{A}^{\top} $ always symmetric? Can you prove the result by using only the result of the previous two exercises?

Yes, since we’re literally just asking whether $ (x) + (y) == x + y $. How? Both , the $ (i, j)^{th} $ and $ (j, i)^{th} $ values of any matrix $ \mathbf{A} $ are being added to each other, making them the same, leading to symmetricity

4. We defined the tensor $ \mathsf{X} $ of shape (2, 3, 4) in this section. What is the output of len(X)? Write your answer without implementing any code, then check your answer using code.

2, since we’re taking the length of a “list” that contains elements of shape (3, 4).

X = torch.arange(2 * 3 * 4, dtype = torch.float32).reshape(2, 3, 4)
len(X)

2

5. For a tensor $ \mathsf{X} $ of arbitrary shape, does len(X) always correspond to the length of a certain axis of $ \mathsf{X} $? What is that axis?

Yes, axis 0

6. Run A / A.sum(axis=1) and see what happens. Can you analyze the reason?

A / A.sum(axis=1)

---------------------------------------------------------------------------

RuntimeError                              Traceback (most recent call last)

Input In [68], in <cell line: 1>()
----> 1 A / A.sum(axis=1)


RuntimeError: The size of tensor a (3) must match the size of tensor b (2) at non-singleton dimension 1

The reason is that the shapes completely mismatch : the very order of the tensors themselves is incompatible, so broadcasting won’t save us

7. When traveling between two points in downtown Manhattan, what is the distance that you need to cover in terms of the coordinates, i.e., in terms of avenues and streets? Can you travel diagonally?

I don’t know what avenues are . But I believe we travel along streets/roads that lead us to our destination. We can’t travel diagonally since there will be things like houses and other buildings/parks/private properties getting in the way

8. Consider a tensor with shape (2, 3, 4). What are the shapes of the summation outputs along axis 0, 1, and 2?

X.sum(axis = 0).shape, X.sum(axis = 1).shape, X.sum(axis = 2).shape

(torch.Size([3, 4]), torch.Size([2, 4]), torch.Size([2, 3]))

The axis along which we reduced got destroyed

9. Feed a tensor with 3 or more axes to the linalg.norm function and observe its output. What does this function compute for tensors of arbitrary shape?

X, torch.linalg.norm(X)

(tensor([[[ 0.,  1.,  2.,  3.],
          [ 4.,  5.,  6.,  7.],
          [ 8.,  9., 10., 11.]],
 
         [[12., 13., 14., 15.],
          [16., 17., 18., 19.],
          [20., 21., 22., 23.]]]),
 tensor(65.7571))

Sum = 0
for item in X.flatten():
    Sum += item ** 2
torch.sqrt(Sum)

tensor(65.7571)

Looks like it simply sums the square of all the elements inside the tensor then takes square root

10. Define three large matrices, say $ \mathbf{A} \in \mathbb{R}^{2^{10} \times 2^{16}} $, $ \mathbf{B} \in \mathbb{R}^{2^{16} \times 2^{5}} $ and $ \mathbf{C} \in \mathbb{R}^{2^{5} \times 2^{16}} $, for instance initialized with Gaussian random variables. You want to compute the product . Is there any difference in memory footprint and speed, depending on whether you compute $ (\mathbf{A} \mathbf{B}) \mathbf{C} $ or $ \mathbf{A} (\mathbf{B} \mathbf{C}) $. Why?

$ (\mathbf{A} \mathbf{B}) \mathbf{C} $ will result in time being $ \mathcal{O}(2^{10} \times 2^{16} \times 2^5 + 2^{10} \times 2^{5} \times 2^{16} ) $

$ \mathbf{A} (\mathbf{B} \mathbf{C}) $ will result in time being $ \mathcal{O}(2^{10} \times 2^{16} \times 2^{16} + 2^{16} \times 2^{5} \times 2^{16} ) $

The latter is much much more expensive because of the algorithms being designed to have complexity of $ \mathcal{O}(n \times m \times k) $ where the matrices $ A $ and $ B $ are of size $ \mathbb{R}^{n \times m} $ and $ \mathbb{R}^{m \times k} $ respectively

11. Define three large matrices, say $ \mathbf{A} \in \mathbb{R}^{2^{10} \times 2^{16}} $ , $ \mathbf{B} \in \mathbb{R}^{2^{16} \times 2^{5}} $ and $ \mathbf{C} \in \mathbb{R}^{2^{5} \times 2^{16}} $. Is there any difference in speed depending on whether you compute $ \mathbf{A} \mathbf{B} $ or $ \mathbf{A} \mathbf{C}^\top $? Why? What changes if you initialize $ \mathbf{C} = \mathbf{B}^\top $ without cloning memory? Why?

A = torch.randn( (2 ** 10, 2 ** 16) )
B = torch.randn( (2 ** 16, 2 ** 5) )
C = torch.randn( (2 ** 5, 2 ** 16) )

%time

temp = A @ B

CPU times: user 2 µs, sys: 0 ns, total: 2 µs
Wall time: 5.96 µs

%time

temp = A @ C.T

CPU times: user 2 µs, sys: 0 ns, total: 2 µs
Wall time: 5.48 µs

%time

temp = A @ B.T

CPU times: user 2 µs, sys: 0 ns, total: 2 µs
Wall time: 5.25 µs



---------------------------------------------------------------------------

RuntimeError                              Traceback (most recent call last)

Input In [101], in <cell line: 3>()
      1 get_ipython().run_line_magic('time', '')
----> 3 temp = A @ B.T


RuntimeError: mat1 and mat2 shapes cannot be multiplied (1024x65536 and 32x65536)

$ \mathbf{A} \times \mathbf{C}^{\top} $ yields better performance due to the layout of data in memory : since the row major format in which data is usually stored in torch usually prefers memory accesses of the same row, when you take transpose of $ \mathbf{C}^{\top} $, it’s not really taking a physical transpose, but a logical one, meaning when we index the trasposes matrix at $ (i, j) $, it just gets internally converted to $ (j, i) $ of the matrix before transposition. Since the elements of the second matrix are accessed column-wise, it is inefficient for this task, but if we have it logically transposed, then the accesses become efficent again, since the data is logically being accessed across rows, ie, columns-wise, but is physically geting accessed across columns, ie, row-wise, since we didn’t actually perform the element swaps, only decided to change indexing under the hood. Hence, the transpose technique works faster

I just don’t understand what is being asked about transposing $ \mathbf{B}^{\top} $. Now the resulting matrix can’t be multiplied with $ \mathbf{A} $ since their shapes are incompatible

12. Define three matrices, say $ \mathbf{A}, \mathbf{B}, \mathbf{C} \in \mathbb{R}^{100 \times 200} $. Constitute a tensor with 3 axes by stacking $ [\mathbf{A}, \mathbf{B}, \mathbf{C}] $ . What is the dimensionality? Slice out the second coordinate of the third axis to recover $\mathbf{B} $ . Check that your answer is correct.

A = torch.randn( (100, 200) )
B = torch.randn( (100, 200) )
C = torch.randn( (100, 200) )

stacked = torch.stack([ A, B, C ])
print(f"{stacked.shape = }")

stacked [ 1 ] == B

stacked.shape = torch.Size([3, 100, 200])





tensor([[True, True, True,  ..., True, True, True],
        [True, True, True,  ..., True, True, True],
        [True, True, True,  ..., True, True, True],
        ...,
        [True, True, True,  ..., True, True, True],
        [True, True, True,  ..., True, True, True],
        [True, True, True,  ..., True, True, True]])

I have no idea why the latex rendering isn’t working

@goldpiggy @mli sorry for pinging like this but can anything be done about this? It’s very disheartening to see all my efforts to write equations in an aesthetically pleasing way turn out like this

Thanks in advance

Edit : I found a link to a post where there seems to be an official plugin to enable latex support. Maybe that can help? Discourse Math - plugin - Discourse Meta

[xavier_porras]

1. The (i,j)-entry of AT is the (j,i)-entry of A, so the (i,j)-entry of (AT)T is the (j,i)-entry of AT, which is the (i,j)-entry of A. Thus all entries of (AT)T coincide with the corresponding entries of A, so these two matrices are [equal.]

2. The (i,j)-entry of AT+BT is the sum of (i,j)-entries of AT and BT, which are (j,i)-entries of A and B, respectively. Thus the (i,j)-entry of AT+BT is the (j,i)-entry of the sum of A and B, which is equal to the (i,j)-entry of the transpose (A+B)T.

3. Given any square matrix A, is A + A⊤ always symmetric? Why?, A has mxn and if A is symetric m=n so A⊤ has nxm where m=n for symetric, so A+A⊤ is simetric

4. len(x) = 2

5. first axis lengh

6. No broadcast chance, last dimension is diferente for both matrix
   x.shape, x.sum(axis=1).shape

7. the norm L2 of vector, pass, pass

8. (torch.Size([3, 4]), torch.Size([2, 4]), torch.Size([2, 3]))

9. Frobenius norm

[block_ramen]

In section 2.3.9. Matrix-Vector Products, why is the row vector $\mathbf{a}^\top_{i}$ represented as a transpose? Or is the transpose symbol there to represent something else?

[ari]

I get the following error when trying to transpose the matrix using A.T
UserWarning: The use of x.T on tensors of dimension other than 2 to reverse their shape is deprecated and it will throw an error in a future release. Consider x.mT to transpose batches of matricesor x.permute(*torch.arange(x.ndim - 1, -1, -1)) to reverse the dimensions of a tensor. (Triggered internally at …/aten/src/ATen/native/TensorShape.cpp:2985.)

When I use x.permute on a 2 x 2 array all is does is make a it a 1 x 4 array.

I can’t seem to get the transpose right.
Thanks!

[Ashkin]

Because typically a vector is considered as a column vector. So $\mathbf{a}^T=[a_0, a_1, a_2, \cdots, a_n]$ ($\mathbf{a}^T$ becomes a row vector.). Now if you expand each element, you get the original matrix.

[cclj]

Ex1-3.

• The transpose of transpose
  

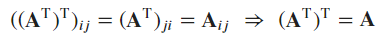
• Commutativity of transpose and addition
  

• Symmetrization of a matrix
  

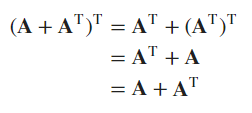
  • The first equality is based on Ex2 (commutativity), and the second equality is based on Ex1 (transpose of transpose);
  • The last equality holds due to the commutativity of the addition operation

Ex4-5.

• The len() method, similar to that in NumPy arrays, returns the first dimension of a given tensor.
• The basis is the magic function __len__ implemented in the corresponding classes (e.g., arrays or tensors).

import torch

X = torch.arange(24).reshape(2, 3, 4)
len(X)

Output:

2

Ex6 & 8

A = torch.arange(6, dtype=torch.float32).reshape(2, 3)
A / A.sum(axis=1)

Output:

---------------------------------------------------------------------------
RuntimeError                              Traceback (most recent call last)
Cell In[3], line 2
      1 A = torch.arange(6, dtype=torch.float32).reshape(2, 3)
----> 2 A / A.sum(axis=1)

RuntimeError: The size of tensor a (3) must match the size of tensor b (2) at non-singleton dimension 1

• The size of A is (2,3), and A.sum(axis=1) yields a reduced summation tensor in shape (2, ).
  • With two tensors of different numbers of axes (different dimensionalities), neither the direct element-wise operation / nor its broadcast version can be performed.

A.shape, A.sum(axis=1).shape

Output:

(torch.Size([2, 3]), torch.Size([2]))

• The operation that this problem really “wants” to perform is probably a column-wise normalization, where each element 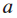is divided by the summation of all elements in the row where 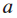lies, so that each row of the resulting tensor sums up to 1. But since the particular dimension to sum has been reduced, the broadcasting scheme will fail.
  • A solution: use keepdims=True to preserve the axis. After the summation, the size of this axis will be 1, but not zero.

A / A.sum(axis=1, keepdims=True)

tensor([[0.0000, 0.3333, 0.6667],
        [0.2500, 0.3333, 0.4167]])

• A closer look at the reduced summation operation

B = torch.arange(24).reshape(2, 3, 4)
B.shape, B.sum(axis=0).shape, B.sum(axis=1).shape, B.sum(axis=2).shape

Output:

(torch.Size([2, 3, 4]),
 torch.Size([3, 4]),
 torch.Size([2, 4]),
 torch.Size([2, 3]))

[cclj]

Ex7.

• In downtown Manhattan, streets are rectilinearly distributed, and one has to travel from point 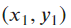to along a trajectory composed of only horizontal and vertical lines.
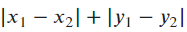  • In such a case, the shortest distance to travel is .
• For a given space with dimension , the Manhattan distance between two points 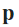and is defined as
  
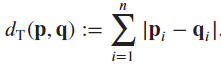
  • This is applicable in signal processing, Machine Learning models, etc.

Ex9.

• By default, the torch.linalg.norm() function computes the Frobenius norm (for more-than-one ordered tensors) or the L2-norm (for one-ordered tensors, or vectors), as per the documentation.
  

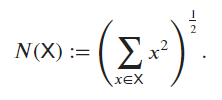
• Below shows an example of a 4-ordered tensor

torch.manual_seed(706)
X = torch.randn(2, 3, 4, 5)
torch.linalg.norm(X), ((X ** 2).sum()) ** 0.5

Output:

(tensor(11.9074), tensor(11.9074))

[cclj]

Ex12.

A = torch.ones(100, 200, dtype=torch.int32)
B = torch.ones_like(A) * 2
C = torch.ones_like(A) * 3
stacked = torch.stack([A, B, C])
stacked.shape

Output:

torch.Size([3, 100, 200])

• By default, the torch.stack() function constructs a new dimension at axis 0, along which the same-sized tensors are stacked, as per the documentation.
  • To slice out B, one indexes 1 in the first axis.

(stacked[1] == B).sum() == B.numel()

Output:

tensor(True)

[sencesco]

Exercise 10: let’s me clarify A,B and C they are same tensor dimension

# Pytorch
import time

# Define matrix dimensions
dim_A = (216, 216)
dim_B = (216, 216)
dim_C = (216, 216)

# Generate random matrices A, B, and C
A = torch.randn(*dim_A)
B = torch.randn(*dim_B)
C = torch.randn(*dim_C)

# Compute (AB)C and measure time and memory
start_time = time.time()
AB = np.dot(A, B)
ABC = np.dot(AB, C)
execution_time_ABC = time.time() - start_time
memory_usage_ABC = ABC.nbytes / (1024 * 1024)  # Convert bytes to MB

# Compute AC^T and measure time and memory
start_time = time.time()
AC_T = np.dot(A, C.T)
execution_time_ACT = time.time() - start_time
memory_usage_ACT = AC_T.nbytes / (1024 * 1024)  # Convert bytes to MB

# Print results
print("(AB)C:")
print("Execution time:", execution_time_ABC, "seconds")
print("Memory usage:", memory_usage_ABC, "MB")
print("\nAC^T:")
print("Execution time:", execution_time_ACT, "seconds")
print("Memory usage:", memory_usage_ACT, "MB")

Ouput:

(AB)C:
Execution time: 0.0015840530395507812 seconds
Memory usage: 0.177978515625 MB

AC^T:
Execution time: 0.0008935928344726562 seconds
Memory usage: 0.177978515625 MB

Time and space complexity

Note: space complexity = memory footprint

• $(AB)C$: They are require 2 times for matrix multiplication as $A$ multiplication $B$ and then $AB$ multiplication $C$ for matrix multiplication. If we are going deeper into the pseudo-code of matrix multiplication:

def multiply_2_matrix(matrix_a, matrix_b):
    rows_a = len(matrix_a)
    cols_a = len(matrix_a[0])
    rows_b = len(matrix_b)
    cols_b = len(matrix_b[0])
    
    if cols_a != rows_b:
        raise ValueError("Number of columns in matrix_a must match the number of rows in matrix_b")
    
    result = [[0] * cols_b for _ in range(rows_a)]
    
    # traveling through all rows of A
    for i in range(rows_a):
        # traveling through all columns of B
        for j in range(cols_b):
            # traveling through all columns of A 
            for k in range(cols_a):
                # at any ij position = sum of i*k
                result[i][j] += matrix_a[i][k] * matrix_b[k][j]
    
    return result

So in matrix multiplication:

$;;;;$ Time complexity = 2 times of operation($A$ x $B$ and then $AB$ x $C$) is $O(i^2j)$ per 1 multiplication → In summary $O(i^2j)$

$;;;;$ Space complexity = $O(ij)$ (They not store new memory in next times operation just update result)

• $AC^T$: They are require 1 times for matrix multiplication as $A$ multi $C^T$ for matrix multiplication. If we are going deeper into the pseudo-code of transpose matrix:

def transpose_matrix(matrix):
    # New list of transpose matrix
    transposed = []
    # traveling through all columns
    for i in range(len(matrix[0])):
        transposed_row = []
        # update column as row
        for row in matrix:
            transposed_row.append(row[i])
        transposed.append(transposed_row)
    return transposed

So in matrix multiplication:

$;;;;$ Time complexity = 1 times of operation($A$ x $C^T$) is $O(i^2j) per 1 multiplication. And 1 times of transpose matrix of C in $O(ij)$. Even though time complexity of $AC^T$ = $(AB)C$ is $O(i^2j)$ but $O(ij)$ of transpose will less than $O(i^2j)$ of multiplication. → In summary $O(i^2j)$

$;;;;$ Space complexity = $O(ij)$ (Even $C^T$ will create new memory but just a tempory memory when multiplication with $A$ will update an store in result memory).

So that why $(AB)C$ need to spend more time $AC^T$ while memory footprint are equal.

[filipv]

My solutions. As a note – it would be nice if this forum had MathJax support! I’m also unable to include more than 2 links or 1 embedded media item as a new user.

Does anyone have a solid answer for #11?

4. 2
5. len(x) always returns the length of the first (outermost) dimension.
6. There’s an error – but if you add keepdim=True, this operation normalizes the columns (such that they add up to one).
7. Manhattan distance (avenues + streets), and sometimes (on Broadway or in the village)!
8. (3, 4), (2, 4), and (2, 3) along axes 0, 1, and 2 respectively.
9. It outputs the l2 norm for vectors, and the frobenius norm for matrices. For arbitrary tensors, it returns the square root of the sum of the squares of the tensor’s elements.
10. For an m x k @ k x n matmul, you perform m * n * (m+n+1) FLOPs. k disappears! So (AB)C is faster than A(BC), since 16 > 5 (and you want to make the larger number “disappear”).
11. I’m not sure about this one. There may be a greater overhead because of different memory access patterns, or some overhead associated with the tranpose itself. If that is the case, initializing C = B^\top would save the cost of memory duplication. I’m not sure what effect this would have on data access patterns.
12. 3 x 100 x 200.

[Sarah]

Exercise 1

import torch 

A = torch.arange(6, dtype=torch.float64).reshape(2, 3)
(A.T).T == A

tensor([[True, True, True],
        [True, True, True]])

Exercise 2

B = A.clone()
A.T + B.T == (A + B).T

tensor([[True, True],
        [True, True],
        [True, True]])

Exercise 3

M = torch.arange(9, dtype=torch.float64).reshape(3, 3)
M + M.T == (M + M.T).T

tensor([[True, True, True],
        [True, True, True],
        [True, True, True]])

Exercise 4

The tensor X has the shape (2, 3, 4), meaning it has 2 elements in the first dimension, each being a tensor of shape (3, 4). Therefore, the output of len(X) is 2, as this function returns the size of the first dimension of a tensor.

X = torch.arange(24).reshape(2, 3, 4)
len(X)

2

Exercise 5

Yes, len(X) will always correspond to the length of the first axis (axis 0).

Exercise 6

try:
    A / A.sum(axis=1)
except Exception as error:
    print(A.shape, A.sum(axis=1).shape, error, sep="\n")

torch.Size([2, 3])
torch.Size([2])
The size of tensor a (3) must match the size of tensor b (2) at non-singleton dimension 1

Notice that A and A.sum(axis=1) have different dimensions, so the operation does not occur. The error, therefore, informs that the division requires the sum vector to be resized to match the dimensions of the original matrix. Like this:

A / A.sum(axis=1, keepdim=True)

tensor([[0.0000, 0.3333, 0.6667],
        [0.2500, 0.3333, 0.4167]], dtype=torch.float64)

Exercise 7

Source: Taxicab geometry and map of Manhattan Center.

Exercise 8

X = torch.arange(24).reshape(2, 3, 4)
X,X.sum(axis=0), X.sum(axis=1), X.sum(axis=2)

(tensor([[[ 0,  1,  2,  3],
          [ 4,  5,  6,  7],
          [ 8,  9, 10, 11]],
 
         [[12, 13, 14, 15],
          [16, 17, 18, 19],
          [20, 21, 22, 23]]]),
 tensor([[12, 14, 16, 18],
         [20, 22, 24, 26],
         [28, 30, 32, 34]]),
 tensor([[12, 15, 18, 21],
         [48, 51, 54, 57]]),
 tensor([[ 6, 22, 38],
         [54, 70, 86]]))

Exercise 9

X = torch.arange(24, dtype=torch.float64).reshape(2, 3, 4)
torch.linalg.norm(X)

tensor(65.7571, dtype=torch.float64)

torch.linalg.norm() computes the Frobenius norm for matrices (2D tensors) and the L2 norm for tensors with more than two dimensions. Thus, the previous result represents the magnitude of the vector in a high-dimensional space formed by flattening the tensor X. Applying this function “forcefully”:

def l2(tensor):
    return torch.sqrt(torch.sum(tensor ** 2))
l2(X)

tensor(65.7571, dtype=torch.float64)

Exercise 10

import psutil
import time

def memory(X, Y):
    start = time.time()
    torch.mm(X, Y)
    memory = psutil.virtual_memory()
    print(f"Total system memory: {memory.total / (1024 ** 3):.2f} GB")
    print(f"Memory used: {memory.used / (1024 ** 3):.2f} GB")
    print(f"Available memory: {memory.available / (1024 ** 3):.2f} GB")
    print(f"CPU usage: {psutil.cpu_percent():.2f}%")
    elapsed = time.time() - start
    print(f"Elapsed time: {elapsed:.2f} seconds\n")

torch.manual_seed(42)
A = torch.randn(2 ** 10, 2 ** 16, dtype=torch.float64)
B = torch.randn(2 ** 16, 2 ** 5, dtype=torch.float64)
C = torch.randn(2 ** 5, 2 ** 14, dtype=torch.float64)

memory(torch.mm(A, B), C)
memory(A, torch.mm(B, C))

Total system memory: 19.23 GB
Memory used: 2.82 GB
Available memory: 15.72 GB
CPU usage: 21.10%
Elapsed time: 0.05 seconds

Total system memory: 19.23 GB
Memory used: 10.82 GB
Available memory: 7.75 GB
CPU usage: 70.70%
Elapsed time: 27.60 seconds

Exercise 11

I believe there is a typographical error in this question because the operation torch(A, B.T) is not possible due to dimension incompatibility. In this case, I did C = C.T (which I think is what the authors actually intended).

torch.manual_seed(42)
C = torch.randn(2 ** 5, 2 ** 16, dtype=torch.float64)

memory(A, B)
memory(A, C.T)

C = C.T
memory(A, C)

Total system memory: 19.23 GB  
Memory used: 3.26 GB  
Available memory: 15.22 GB  
CPU usage: 12.00%  
Elapsed time: 0.07 seconds

Total system memory: 19.23 GB  
Memory used: 3.28 GB  
Available memory: 15.22 GB  
CPU usage: 15.00%  
Elapsed time: 0.06 seconds

Total system memory: 19.23 GB  
Memory used: 3.27 GB  
Available memory: 15.22 GB  
CPU usage: 9.50%  
Elapsed time: 0.07 seconds

• Theoretically, the operations torch.mm(A, B) andtorch.mm(A, C.T) should have similar performance in terms of computational complexity, but differ in memory access due to the data orientation of C.T. It was expected that transposition would negatively affect efficiency due to non-sequential memory access. However, the time difference between torch.mm(A, B) and torch.mm(A, C.T) is minimal. Perhaps the internal optimization of PyTorch for transpose operations is quite effective, minimizing the theoretically negative impact of memory transposition.

• Pre-transposing Cand performing the multiplication with A shows a runtime comparable to torch.mm(A, B), with slightly reduced CPU usage. The reduction in CPU usage may be due to the elimination of the need for dynamic transposition during multiplication, indicating that pre-processing C might be beneficial from the perspective of reducing CPU load, despite not significantly impacting runtime.

Exercise 12

torch.manual_seed(42)
A = torch.randn(100, 200, dtype=torch.float64)
B = torch.randn(100, 200, dtype=torch.float64)
C = torch.randn(100, 200, dtype=torch.float64)
torch.stack([A,B,C]).shape, torch.stack([A,B,C])[1] == B

(torch.Size([3, 100, 200]),
 tensor([[True, True, True,  ..., True, True, True],
         [True, True, True,  ..., True, True, True],
         [True, True, True,  ..., True, True, True],
         ...,
         [True, True, True,  ..., True, True, True],
         [True, True, True,  ..., True, True, True],
         [True, True, True,  ..., True, True, True]]))