Forward Propagation, Backward Propagation, and Computational Graphs

English Version
1

http://d2l.ai/chapter_multilayer-perceptrons/backprop.html

2

small typo: “requried” -> “required”

Thanks again for the great resource you’ve put together!

3
  1. n×m
  2. 4-7-e
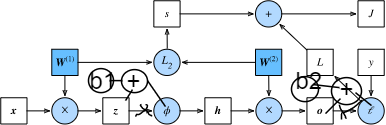
  3. How to compute the memory footprint? What is in the memory?
  4. Computational Graph of Backpropagation? Try to track all latest two times’ calculate.
  5. Now, I can’t. How to parallelly train?
    Good for updating quickly.Easy to fall into a local extremum.
4

Why does the backpropagation (I mean the way of calculating gradients) have to go in the opposite direction of forward propagation? Can’t we calculate gradients in the forward propagation, which cost less memory?

6

The purpose of backward propagation is to get near to, even same as the labels we gave.
We only calulate gradients when we know the distance of prediction and reality.
This is the backward propagation what really does.

1 Like
7

Hi @RaphaelCS, great question! Please find more details at https://mxnet.apache.org/api/architecture/note_memory to see how we manage memory efficiently.

2 Likes
8

Thanks for the reference !

9

I want to ensure some kind of achievement about back propagation which is equivalent to the normal way from my perspective. I think we could do merely the partial derivation and value calculation during the forwarding pass and multiplication during the back propagation. Is it an effective, or to say another equivalent way to achieve BP? Or they are different from some aspects?

10

I think we could do merely the partial derivation and value calculation during the forwarding pass and multiplication during the back propagation.

What is different with BP?

11

BP do the partial derivation during back propogation step rather than the forwarding step? I just want to ensure wether these two methods have the same effect. Thanks for your reply.

12

The most important thing, in my opinion, is to find out which elements we need to calculate the partial derivation. Back propogation is only the way to find it. Am I right?

1 Like
13

I agree with you and now I think two ways mentioned above are actually the same .

14

For BP to calculate the gradients with respect to the current loss, we need to actually do the forward pass and get the loss with the current parameters, right ? How can BP be done in the forward pass if we don’t even have the loss for the current parameters.

15

In my opinion, we can calculate the partial derivative of h1 w.r.t. x and the partial derivative of h2 w.r.t.h1, then we can obtain the partial derivative of h2 w.r.t. x by multiplying the previous two partial derivatives. I think these calculations can all be done in forwarding steps. (x refers to input, h1 and h2 refer to two hidden layers)
If I’m not mistaken, we can keep calculating in this manner until the loss, thus all in forward stage.

BTW, perhaps this method requires much more memory to store the intermediate partial derivatives.

16

Great discussion @Anand_Ram and @RaphaelCS ! As you point out the memory may explode if we save all the immediate gradient. Besides, some of the saved gradients may not require for calculation. As a result, we usually do a full pass of forward propagation and then backpropagate.

17

This link was very interesting in explaining some of mxnet’s efficiency results.

18

4.7.2.2

dJ/db_2 =
    prod(dJ/dL, dL/do, do/db_2)
    
    prod(1, 2(o - y), 1)

    2(o - y)

dJ/db_1 = 
    prod(dJ/dL, dL/do, do/dh, dh/dz, dz/db_1)    

    prod(1, 2(o - y), w_2, phi'(z), 1)

    prod(2(o - y), w_2, phi'(z))

Do these bias terms look ok?

19

seems correct in case of softmax regr.
but where does the coefficient ‘2’ above come from? @six

20

all figures are missed at that link, is it the problem w.r.t. my network env?

21

After looking at: https://math.stackexchange.com/questions/2792390/derivative-of-euclidean-norm-l2-norm

I realize:

d/do l2_norm(o - y)

d/do ||o - y||^2

d/do 2(y - o)

Here’s a good intuitive explanation as well from the top answer at the above link (x is o here):
“points in the direction of the vector away from y towards x: this makes sense, as the gradient of ∥y−x∥2 is the direction of steepest increase of ∥y−x∥2, which is to move x in the direction directly away from y.”