Is there someone can share the idea about question 6? thx
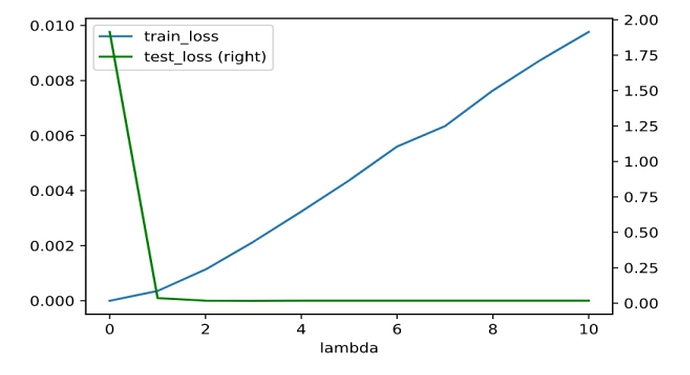
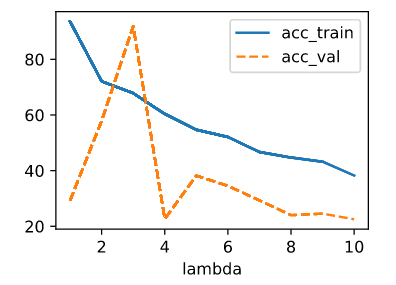
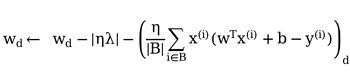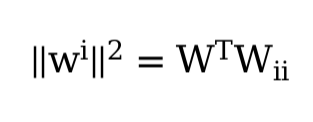It seem that a model with no regularization is better than a model with regularization in my case. Although the norm of the weights is significantly lower in the model with regularization, the plots are better in the unregularized one. Another problem is that the loss in my validation data is lower than the training loss. Here is my code:
import torch
from torch.utils.data import TensorDataset, DataLoader
import matplotlib.pyplot as plt
def synthetic_data(true_w, true_b, n):
X = torch.normal(0, 0.01, (n, len(true_w)))
y = torch.matmul(X, true_w) + true_b
y += torch.normal(0, 0.001, y.shape)
return X, y.reshape((-1, 1))
def load_array(array, batch_size, is_train=False):
''' Change array to a torch data iterator '''
dataset = TensorDataset(*array)
return DataLoader(dataset, batch_size=batch_size, shuffle=is_train)
n_train, n_test, n_inputs, batch_size = 20, 100, 200, 5
true_w = torch.ones((n_inputs, 1)) * 0.01
true_b = 0.05
train_data, train_labels = synthetic_data(true_w, true_b, n_train)
train_iter = load_array((train_data, train_labels), batch_size, is_train=True)
test_data, test_labels = synthetic_data(true_w, true_b, n_test)
test_iter = load_array((test_data, test_labels), batch_size)
# build the model
def linreg(X):
return X@W + b
# initialize the weights
W = torch.normal(0, 1, (n_inputs, 1), requires_grad=True)
b = torch.zeros(1, requires_grad=True)
# define the loss function
def MSELoss(y_hat, y):
return (y_hat - y) ** 2 / 2
# define the L2 regularization term
def L2_penality(W):
return torch.norm(W) / 2
# Define the optimizer
def SGD(params, batch_size):
with torch.no_grad():
for param in params:
param -= lr * param.grad / batch_size
param.grad.zero_()
class Accumulator:
def __init__(self, n):
self.data = [0.0] * n
def add(self, *args):
self.data = [a + float(b) for a, b in zip(self.data, args)]
def reset(self):
self.data = [0.0] * len(self.data)
def __getitem__(self, index):
return self.data[index]
def evaluate(data_iter):
metric = Accumulator(2)
with torch.no_grad():
for X, y in data_iter:
l = MSELoss(linreg(X), y)
metric.add(float(l.sum().item()), len(y))
return metric[0] / metric[1]
# Write the training loop
epochs, lr = 100, 0.003
weight_decay = 0
train_loss = []
val_loss = []
train_metric = Accumulator(2)
for epoch in range(epochs):
for X, y in train_iter:
l = MSELoss(linreg(X), y) + weight_decay * L2_penality(W)
l.sum().backward()
SGD([W, b], batch_size)
train_metric.add(float(l.sum().item()), len(y))
train_loss.append(train_metric[0] / train_metric[1])
train_metric.reset()
# test the validation loss
l = evaluate(test_iter)
val_loss.append(l)
## print("Epoch {}/{} loss: {:.5f} val_loss: {:.5f}".format(epoch+1, epochs, train_loss[-1], val_loss[-1]))
print("Weight Norm: ", torch.norm(W).item())
plt.plot(range(len(train_loss)), train_loss, label='Train loss')
plt.plot(range(len(val_loss)), val_loss, label='Validation loss')
plt.xlabel("Epochs")
plt.ylabel("Loss")
plt.title("Training and validation loss")
plt.legend()
plt.show()First post! 
Thanks for this amazing book.
Also, I tried to plot train and test loss vs the choice of lambda. We can see that the training loss increases and test loss first decreases then stays mostly constant (see exact values below)
So, is the first value where test loss decreases before staying stagnant (i.e. lambda=1) is the best regularization parameter for this problem @goldpiggy can you suggest if this is a ok heuristic?
srno lambda train_loss test_loss
0 0 2.360348e-13 1.914223
1 1 3.561247e-04 0.035403
2 2 1.136713e-03 0.018138
3 3 2.143079e-03 0.017133
4 4 3.240126e-03 0.017512
5 5 4.373294e-03 0.017590
6 6 5.604185e-03 0.017622
7 7 6.343381e-03 0.017295
8 8 7.639927e-03 0.017984
9 9 8.753147e-03 0.017798
10 10 9.767077e-03 0.017654
#https://stackoverflow.com/questions/42704283/adding-l1-l2-regularization-in-pytorch
def l1_norm_with_abs(w):
return torch.abs(w).sum()Exercises and my answers
- Experiment with the value of λ in the estimation problem in this section. Plot training and
test accuracy as a function of λ. What do you observe?
- as we increase wd it is making better train and test loss graph
- Use a validation set to find the optimal value of λ. Is it really the optimal value? Does this
matter?
- the minimum loss is 0.02 at wd = 21-5 = 16. It is th eoptimal value for the validation set.
- What would the update equations look like if instead of ∥w∥
2 we used ∑
i
|wi
| as our penalty
of choice (L1 regularization)?
- It is strangely coming as linear
# training for l1 norm
model = nn.Sequential(nn.Linear(num_inputs, 1))
for param in model.parameters():
param.data.normal_()
print(l1_norm(param.detach()))
loss = nn.MSELoss()
optimizer = torch.optim.SGD(model.parameters(), lr = 0.03)
valid_loss_array = []
for epoch in range(20):
current_loss = 0
current_number = 0
for X, y in valid_dataloader:
l = loss(model(X),y) - l1_norm_with_abs(model[0].weight)
optimizer.zero_grad()
l.backward()
optimizer.step()
current_loss += l.detach()
current_number += len(y)
valid_loss_array.append(current_loss/current_number)
plt.plot(range(20), valid_loss_array)
plt.grid(True)
plt.show()
(cant upload the graph here only onw pic per post)
- We know that ∥w∥
2 = w⊤w. Can you find a similar equation for matrices (see the Frobenius
norm in Section 2.3.10)?
- This is Frobenius norm: f(αx) = |α|f(x). I dont understand.
- Review the relationship between training error and generalization error. In addition to
weight decay, increased training, and the use of a model of suitable complexity, what other
ways can you think of to deal with overfitting?
- larger data size, dropouts
- In Bayesian statistics we use the product of prior and likelihood to arrive at a posterior via
P(w | x) ∝ P(x | w)P(w). How can you identify P(w) with regularization?
- you ask good question but me no understand. how to get to p of w.
hi can how are you getting this graph? mine is at loggerheads with yours
- In Bayesian statistics we use the product of prior and likelihood to arrive at a posterior via 𝑃(𝑤∣𝑥)∝𝑃(𝑥∣𝑤)𝑃(𝑤). How can you identify 𝑃(𝑤) with regularization?
@goldpiggy Hi, 𝑃(𝑤∣𝑥)P(x) = 𝑃(𝑥∣𝑤)𝑃(𝑤). Here, P(w|x), P(x), P(w) can be acquired through statistics, so, P(w) can be found if we assume a linear model between P(w|x) *P(x) and p(x|w).
Is it correct?
Even I have no clue about this question.
I guess 4th will be trace(X’X) where X’ = X transpose
1 Like
HI I still didntget it, I am really challenged at maths I think! XD Hey but are you following the book ? I was lookingfor peoplegoing through this book !
Yes, I am going through the book. Currently in chapter 5.
For this problem you can look at trace of the matrix.
1 Like
For this, I think that this will involve proving it through log-likelihood method. if we assume P(w) to be normal distribution with mean 0 and variance = sigma^2, we might be able to derive the L2 regularization using Max Likelihood
I would love some insight into problem 6! I can’t make any headway. Loving the book so far. Thanks
I think this post does a good job at discussing Q6
Here are my opinions about the exs.
ex.1
I close the lot in d2l.Module.
@d2l.add_to_class(d2l.Module)
def training_step(self, batch):
l = self.loss(self(*batch[:-1]), batch[-1])
#self.plot('loss', l, train=True)
return l
@d2l.add_to_class(d2l.Module)
def validation_step(self, batch):
l = self.loss(self(*batch[:-1]), batch[-1])
#self.plot('loss', l, train=False)
return l
Then I use this code snippet to test lambda from 1 to 10
import numpy as np
data = Data(num_train=100, num_val=100, num_inputs=200, batch_size=20)
trainer = d2l.Trainer(max_epochs=10)
test_lambds=np.arange(1,11,1)
board = d2l.ProgressBoard('lambda')
def accuracy(y_hat, y):
return (1 - ((y_hat - y).mean() / y.mean()).abs()) * 100
def train_ex1(lambd):
model = WeightDecay(wd=lambd, lr=0.01)
model.board.yscale='log'
trainer.fit(model, data)
y_hat = model.forward(data.X)
acc_train = accuracy(y_hat[:data.num_train], data.y[:data.num_train])
acc_val = accuracy(y_hat[data.num_train:], data.y[data.num_train:])
return acc_train, acc_val
for item in test_lambds:
acc_train, acc_val = train_ex1(item)
board.draw(item, acc_train.to(d2l.cpu()).detach().numpy(), 'acc_train', every_n=1)
board.draw(item, acc_val.to(d2l.cpu()).detach().numpy(), 'acc_val', every_n=1)
The output of accuracy of different lambda goes like this:
ex.2
I think there may be an analytical solution of lambda if the weights w have already been set after training, and the validation set is fixed, but this procedure gives no credit to any different validation set, so this kind of optimal makes no sense.
I think it doesn’t matter if the lambda is optimal, cause in practice, I can test a set of options and choose one that is good enough to be my lambda.
ex.3
ex.4
ex.5
I think if I can’t narrow gap between training error and generalizing error, there is also a great chance to reach overfitting, so I may use cross validation to make more use on the data I have now.
ex.6
Regularization adds some limit on the parameters of a model before the training, that is somehow like a prior in Bayesian estimation.
1 Like
what is a scratch? please define scratch.
I’m seeing a similar L2 norm of the weights between the example without regularization and the example using ‘weight_decay’ in torch.optim.SGD.
The examples in the book show this as well, whereas the L2 norm of the weights is 10 times smaller for the WeightDecayScratch using a lambda of 3.
Why might we expect this?
I am trying to implement weight decay from scratch, however no matter what I set lambda to, I notice the validation loss is always constant. Is there something wrong with my code?
class Data():
def init(self, num_train, num_val, num_inputs, batch_size):
self.batch_size = batch_size
n = num_train + num_val
self.X = torch.randn(n, num_inputs)
noise = torch.randn(n, 1) * .01
w, b = torch.ones((num_inputs, 1)) * .01, .05
self.y = torch.matmul(self.X, w) + b + noise
self.num_train = num_traindef get_trainloader(self): tensorData = TensorDataset(self.X[:self.num_train], self.y[:self.num_train]) return DataLoader(tensorData, batch_size=self.batch_size, shuffle=True) def get_testloader(self): tensorData = TensorDataset(self.X[self.num_train:], self.y[self.num_train:]) return DataLoader(tensorData, batch_size = self.batch_size, shuffle = False)class WeightDecay():
def init(self, num_inputs, lambd, lr):
self.num_inputs = num_inputs
self.lambd = lambd
self.lr = lr
self.net = nn.LazyLinear(1)
self.net.weight.data.normal_(0, .01)
self.net.bias.data.fill_(0)def forward(self, x): return self.net(x) def loss(self, yhat, y): loss_fun = nn.MSELoss()(yhat, y) L2_reg = self.lambd * ((self.net.weight ** 2).sum() / 2) return loss_fun + L2_reg def configure_optimizer(self): return torch.optim.SGD(self.net.parameters(), self.lr, weight_decay=0)data = Data(num_train=20, num_val=100, num_inputs=200, batch_size=5)
model = WeightDecay(200, lambd=0.1, lr=0.01)
optim = model.configure_optimizer()
train_data = data.get_trainloader()
test_data = data.get_testloader()for i in range(10):
train_loss = 0
for X, y in train_data:
preds = model.forward(X)
lossfun = model.loss(preds, y)
train_loss += lossfun
optim.zero_grad()
lossfun.backward()
optim.step()with torch.no_grad(): test_loss = 0 for X, y in test_data: preds = model.forward(X) lossfun = model.loss(preds, y) test_loss += lossfun print(f"Avg loss for epoch {i + 1} on train is {train_loss / len(train_data)}") print(f"Avg loss for epoch {i + 1} on test is {test_loss / len(test_data)}")
- With greater values of
\lambda, the validation loss goes down far more quickly in early epochs. But no matter how large my setting of\lambda, the validation loss doesn’t seem to go far below 10e-2. For extremely large values, the model fails to converge at all. - The final error continues going down for values of
\lambdawell into the range of 10-50! But in practice, I’m not sure you’d want to use a value so extreme - this example is somewhat contrived, and exaggerates the effect of weight decay. Using values this large in practice would hurt the model’s capacity. - Using
\|\mathbf w\|^2, our update to each parameterw_iis equivalent to\eta \lambda \cdot \mathbf w_i. If we used|\mathbf w|, our updates would not scale relative to the weights, and would be a constant\eta \lambdatimes the sign of w. \| A \|_F^2 = \text{trace}(A^T A). Intuitively, the diagonal entries on the gram matrix of A are where the dot product of each column with itself is located - these are the sums of the squares of each column. When we add them up, all entries are included.- More training data, greater diversity of data (possibly including data augmentation), and other forms of added stochastic noise - for example, the slight stochasticity introduced by batch norm layers tends to regularize the model. This is outside the scope of this chapter, but dropout and early stopping can also help.
- In a basic sense, simpler weights are ‘more likely’, and regularization is a means of increasing our P(w), and therefore the posterior probabilities. Further, we can draw a connection between our prior on the weights and the form of regularization we ought to use - if we assume each weight is drawn from a Gaussian distribution with a mean of zero, minimizing the negative log-likelihood of the weights would suggest penalizing a term proportional to the squared norm of w. Analogously, assuming a Laplacian distribution of the weights, minimizing the negative log-likelihood of the weights suggests penalizing a term proportional to the sum of their absolute values - the L1 norm!