Weight Decay

English Version pytorch
1

https://d2l.ai/chapter_linear-regression/weight-decay.html

2

In 4.5.4. Concise Implementation

4-5
4-51609×684 73.2 KB

Typographical error！？

3

Animator:
http://d2l.ai/chapter_linear-networks/softmax-regression-scratch.html?highlight=d2l%20animator
http://d2l.ai/_modules/d2l/torch.html#set_axes
https://matplotlib.org/3.2.1/api/_as_gen/matplotlib.axes.Axes.set_ylim.html

1 Like
4

4.5.1. Squared Norm Regularization

Whether we include a corresponding bias penalty b^2 can vary across implementations, and may vary across layers of a neural network. Often, we do not regularize the bias term of a network’s output layer.
Can you explain b^2 in detail?

5

Hi @StevenJokes, thanks for the feedback, we will fix it!

6

Hi @StevenJokes

4.5.1. Squared Norm Regularization

Whether we include a corresponding bias penalty b^2 can vary across implementations, and may vary across layers of a neural network. Often, we do not regularize the bias term of a network’s output layer. Can you explain b^2 in detail?

Great question! I hardly ever see $b^2$ Generally, applying weight decay to the bias units usually makes only a small difference to the final network.

7

So it just means that bias penalty is not negative?
b is not same as the b in wx+b?

8

@goldpiggy
I tried to implement the code for train_concise on my own and my loss kept increasing exponentially instead of decreasing:
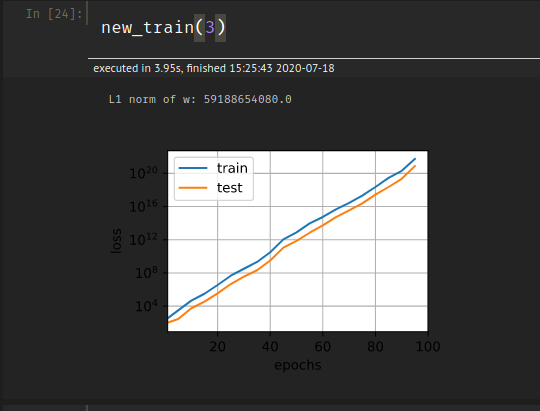
image

Here is my code:

def new_train(lambd):
net=nn.Sequential(nn.Linear(num_inputs,1))
for param in net.parameters():
    param.data.normal_()
loss=nn.MSELoss()
num_epochs=100
lr=0.03
trainer=torch.optim.SGD([{"params":net[0].weight,'weight_decay':lambd},
                         {"params":net[0].bias}],lr=lr)
animator = d2l.Animator(xlabel='epochs', ylabel='loss', yscale='log',
                        xlim=[1, num_epochs], legend=['train', 'test'])
for epoch in range(num_epochs):
    for X,y in train_iter:
        with torch.enable_grad():
            trainer.zero_grad()
            l=loss(net(X),y)
        l.backward()
        trainer.step()
    if epoch%5==0:
         animator.add(epoch, (d2l.evaluate_loss(net, train_iter, loss),
                             d2l.evaluate_loss(net, test_iter, loss)))
print('L1 norm of w:', net[0].weight.norm().item())

I compared my code to the code given in the book to find where I am going wrong but I can’t figure out where I made an error and what is causing this to happen.

Intersestingly, if I increase the value of lambd to say 10, I get low generalization error but the train accuracy seems to be somewhat erratic:
image

Any ideas on this as well?

9

Hey @Kushagra_Chaturvedy, the learning rate is 0.003, while yours is different. Tuning learning rate is kind of tricky, not too small and not too high.

10

Ok, I didn’t know that the learning rate could cause this much disparity in results. Thanks!

11

Is b in b^2 same as the b in wx+b?

12

I think the idea is that W is a really high-dimensional vector because there are so many weights. b is relatively low-dimensional, so regularizing b has a much smaller effect.

1 Like
13

Hello. I have two questions about this notebook. (1) Do I understand correctly that “weight decay” is a generic term for any regularization that involves adding some kind of norm of W (regardless of which norm) to the loss? (2) Is it not possible to add L1 regularization to the optim.SGD input? The docstring only lists L2 norm.

Thanks!

14

Great question! Weight decay ideally should be mathematically equivalent to L2 Regularization. But be carefully when you implement it in code, this article indicates that different frameworks might be slightly different.

1 Like
15

You are maybe right.
Does that mean we can use w and b as bias penalty at the same time or separately?

16

I think it’s possible. Can we add? @goldpiggy

17

Hi @StevenJokes and @Steven_Hearnt, great questions! L1 regularization is applicable if you specify how to handle the in-differentiable case (x=0) .

18

Hi @StevenJokes, I might be late to the party but would like to take a stab at it from a theoretical point of view rather than practical (which has already been covered). If we regularize the bias term (b) by adding the penalty term b^2, the network would end up learning a very small value of bias term in the case where we constraint the model a lot (i.e. lambda is very big). In such a case, model would not have any average value and thus it would be predicting some value near to zero every time. So, in order to avoid such a scenario, maybe bias term isn’t regularized in the last layer.

1 Like
19

Why
“the network would end up learning a very small value of bias term”?

What does your “lambda” mean?

20

Lambda is the constraint imposed on the L2 norm in the loss function. It is defined in 4.5.2. If we set lambda to a very large number and include bias term in the L2 norm as well, gradient descent will set bias term to an extremely small number as well. All of this is mentioned in the section 4.5