Accidentaly put 0.1 learning rate, and always got nan value for L2 norm of w in scratch implementation. I want to know where would the computation part fail but could not find to get the answer. Anyone know? Thank you.
Please consider a more general definition for weight decay in this chapter -
you can refer to the findings of - ‘DECOUPLED WEIGHT DECAY REGULARIZATION - Ilya Loshchilov & Frank Hutter’
- Experiment with the value of λ in the estimation problem in this section. Plot training and
test accuracy as a function of λ. What do you observe?
Answer: With growth of lambda coeff of L2 regularization, test error decrease to certain level
![Screenshot from 2021[poll type=regular results=always public=true chartType=pie]
- Are these the correct answers?
- Are these the NOT correct answers?
[/poll]
-09-04 09-53-07|404x500](upload://u7gRfc1EAVn8H8oIB0m0OQ0CVYK.png)
- Use a validation set to find the optimal value of λ. Is it really the optimal value? Does this
matter?
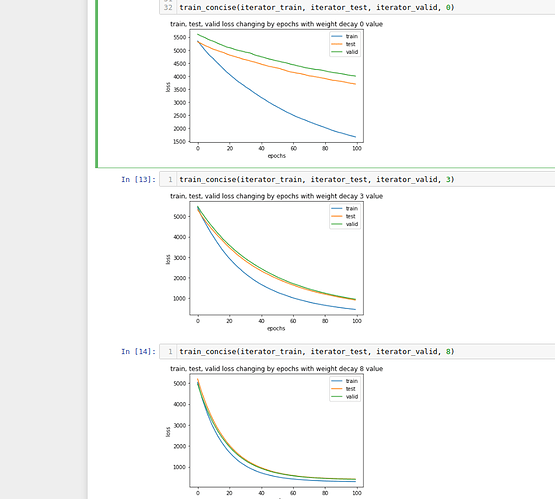
Answer: Created Train and Holdout set, then split train in to training and test set. Find that Holdout loss is similar to Test after a weight decay become more than 1. In you increase weight decay Holdout and Test loss possibly converge. Maybe it is due to nature how data is generated by d2l.synthetic_data
-
What would the update equations look like if instead of ∥w∥ 2 we used i |w i | as our penalty
of choice (L 1 regularization)?def lasso_l1(w):
return (np.abs(w)).sum() / 2 -
Review the relationship between training error and generalization error. In addition to
weight decay, increased training, and the use of a model of suitable complexity, what other
ways can you think of to deal with overfitting?
Answer
- Cross validation including random sampling
- Train on more data
- Feature selection
- Reduce dimensions with e.g. PCA
- For tree based algorithms, play with hyper params like depth, pruning, number of leaves …
- Dropout (in the next chapter)