https://zh.d2l.ai/chapter_recurrent-neural-networks/bptt.html
中文版什么时候更新接下来章节呢?谢谢,辛苦。
这里可以看到一部分最新的章节,你也可以加入进来,一起翻译一些章节。
come on!
天书。。。。。。。。。。。。。。。。。。。。。
2::根据数学期望的性质E[AX+B] = B+AE[X]很容易计算出来
3:T是最后一个时间步。对于hT的计算图为L ← oT <—hT * WT, 因此不需要累加
书中的公式最关键就是通过计算图(8.7.2)来看,需要计算L对哪一个变量或参数的梯度时,就去图中找到他,看他向外的箭头到L的路径有几条,这样就好理解公式,这也是反向传播算法的核心,另外,是不是用求和符号是因为,对于单时间步而言,求偏导时将其他变量视为常数,只有一个变量,比如L对o_t求偏导时就是这样;而在求L对Wqh的偏导时,有T条路径,每一个路径上的o_t都是变量,所以有求和符号。总结下来其实就是:链式法则、反向传播和复合函数求偏导。个人见解,如有错误欢迎指正。
我还以为就我一个人这样。。。。。。。。。。。。。。。。。。。。。。。。。
不懂,第二点能不能详述细节呢???没办法按你的说法代入
第三个问题:不求和是因为对hT(T时间步)求偏分,而前面那个是对所有时间步求偏分
第1问:
由$ Mv_i = \lambda_i v_i $得
$$ M^k v_i = M^(k-1) M v_i = M^(k-1) \lambda_i v_i = … = \lambda_i^k v_i$$
第2问:
将$ x $分解到特征向量$ v_i $构成的空间中,有
$$ x = sum( a_i v_i, from i = 1 to n) $$
于是
$$ M^k x = M^k sum( a_i v_i, from i = 1 to n) $$
$$ = sum( a_i M^k v_i, from i = 1 to n) $$
$$ = sum( a_i \lambda_i^k v_i, from i = 1 to n) $$
因为 $ \lambda_1 $ 最大,所以 $ \lambda_1 >>>> \lambda_i $
也就是说,$ M^k x $ 分解到特征向量$ v_i $构成的空间中后,$ v_1 $ 对应的系数远远大于其他项,因此近乎平行
第二题:
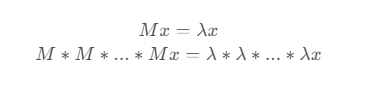
第二问是因为变量的期望是1,而zt与其上一个式子相比只是在其后半部分乘上了变量,那么zt的期望就是与上式相同
就是比如z = a + bx,那么E(z) = E(A) + E(bx) = E(A) + E(b)*E(x),又因为E(A) = A, E(B) = B,E(x) = 1,所以带入就是E(z) = a+b就是最后书上的结果
真实,不知道为啥每个字都看得懂,连一块就不懂了。
got it。这个E[ ξt] =1又怎么来的?
第四题:由于梯度计算中也包含这种连乘操作,最终的计算结果将随着时间不的增加逐渐与权重矩阵的最大特征值所对应的特征向量保持平行,使得梯度下降方向不变。
就是随机删一些梯度数据,只要不是删的太过分,梯度还是近似的