知乎有个老哥介绍了原理，可以看看： 就是他！让你的python内核莫名挂掉 | KMP_DUPLICATE_LIB_OK=TRUE 的始作俑者 - 知乎 (zhihu.com)
请问，这里的反向传播过程中，为什么使用l.sum().backward()而不是l.mean().backward()呢，小批量梯度下降中梯度应该对样本求均值吧？还是说nn.optim.Adam优化器中会求均值之后再更新参数呢？
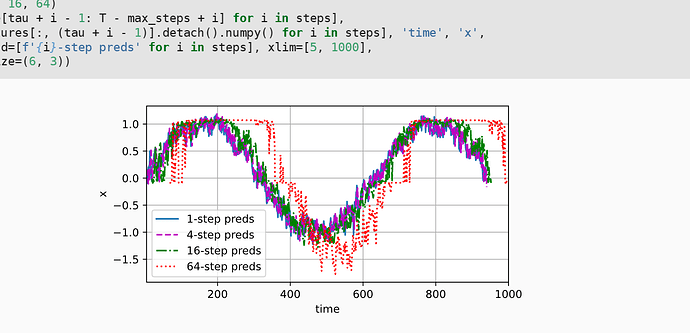
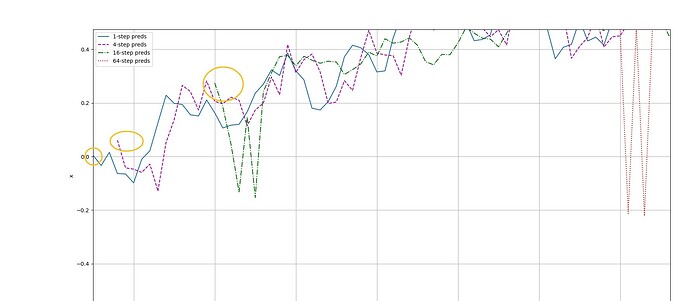
由于这段测试代码，在用 “i”向前迭代的过程中，使得时间向前延max_setps移动了
因此导致看起来16-step preds与原x产生了较大的偏差，其实将相位对准后会发现16-step preds拟合得还是不错的呢 
# 列i（i>=tau）是来自（i-tau+1）步的预测，其时间步从（i）到（i+T-tau-max_steps+1）
for i in range(tau, tau + max_steps):
features[:, i] = net(features[:, i - tau:i]).reshape(-1)
1 Like
感觉对于梯度来说，在这个模型上，sum和mean是等价的，不影响梯度计算
我认为这段翻译的似乎有些问题：
这两种情况都有一个显而易见的问题：如何生成训练数据？ 一个经典方法是使用历史观测来预测下一个未来观测。 显然，我们并不指望时间会停滞不前。 然而，一个常见的假设是虽然特定值 $x_t$ 可能会改变， 但是序列本身的动力学不会改变。 这样的假设是合理的，因为新的动力学一定受新的数据影响， 而我们不可能用目前所掌握的数据来预测新的动力学。 统计学家称不变的动力学为静止的 （stationary）。 因此，整个序列的估计值都将通过以下的方式获得：
这里序列的“动力学”我怎么都理解不了，去翻了英文版，实际上是dynamics of the sequence ，所以我认为翻译成序列的动态特征似乎更能清楚地表达序列随时间变化的特点。
2 Likes
我也感觉，他一开始创建features时候的是(T-tau,tau),这个实际上是(996,4)的数组，没有997个样本，因此它才那么写的，实际相当于(996,997,998,999)这一组样本无法使用，因为999需要作为(995,996,997,998)这一组的label
loss不再明显下降就好了，在5个epoch后loss已经收敛在0.05附近，是很低的值了
loss = nn.MSELoss(reduction='none')
l.sum().backward()
改写成
loss = nn.MSELoss(reduction='sum')
l.backward()
训练结果完全不一样，原因是什么？
epoch 1, loss: 0.852841
epoch 2, loss: 0.778558
epoch 3, loss: 0.758861
epoch 4, loss: 0.829508
epoch 5, loss: 0.800305
请问在x = torch.sin(0.01 * time) + torch.normal(0, 0.2, (T,))这一行代码中，为什么torch.normal可以接受(T,)这样一个元组作为参数传递呢
999要作为最后一行的label，最后一行的feature只能是[995, 996, 997, 998]，而第一行的feature是[0, 1, 2, 3]，所以总行数是996，features.shape是[996, 4]
为什么不同的实现曲线图会差这么多？代码逻辑相同，训练结果差距这么大？
pytorch与tensorflow曲线形态非常不同
感觉不是，理论上feature[i,j+tau]的含义是 j步预测的i得到的值是feature[i,j+tau]
但是实际上这里第996行实际上是（995，996，997，998），正好使用999作为label。所以这个写法是对的喵
原意拆解与解释
- 核心问题：怎么得到训练数据？
在训练一个预测时间序列（比如 RNN）的模型时，我们要有“输入—输出”成对的样本。
一个经典的办法就是：
- 用历史观测数据（过去的几个时间点）作为输入，
- 预测下一个未来的观测值作为输出。
- 时间在变化，规律也可能变化
现实世界并不是静止的，未来的规律可能会和过去不同，这就是所谓的“概念漂移”（concept drift）问题。
但是，为了能训练模型，我们通常假设：
- 虽然具体的数值会随着时间变化，
- 但生成这些数值的动力学规律（动态模式） 是相对稳定的。举例：股市每天的价格会变，但价格波动的统计特性、周期性等短期内可能相对稳定。
- 为什么这个假设是合理的？
- 如果动力学真的发生变化，那一定是因为有了新的外部影响或数据，
- 而这些新规律，我们用现在的历史数据是无法提前知道的，
- 所以只能在现有的规律假设下建模。
- “动力学不变”在统计学里的说法：平稳性（stationary）
- 平稳序列：统计特征（均值、方差、相关性等）不随时间变化。
- 这是假设 RNN 或时间序列模型能有效工作的前提之一。
- 训练方法总结
在这个假设下，我们可以用整条序列的数据，构建很多训练样本：
python-repl
复制编辑
(历史1, 历史2, 历史3) → 预测下一个值
(历史2, 历史3, 历史4) → 预测下一个值
...
如果是连续的数值，用回归模型；
如果是离散的对象（如单词序列），用分类器来预测下一个符号。
更流畅的改写版本（保留原意，去掉生硬感）：
在构建 RNN 或其他时间序列预测模型时，一个核心问题是如何获得训练数据。一个常见做法是：利用过去的观测数据来预测下一个时间点的值。虽然现实中时间和数据都会变化，但我们通常假设，数据背后的动态规律在一段时间内是稳定的（平稳性假设）。这是因为，如果规律真的发生了变化，那一定由新的外部信息驱动，而这种变化无法用现有数据预测。在平稳性假设下，我们可以将整个序列分割成许多“历史窗口 → 下一个值”的训练样本。如果预测的是连续值，我们用回归模型；如果预测的是离散符号（如单词），我们用分类模型。
（这是改写原文8.1节末尾的如下段落。）
“这两种情况都有一个显而易见的问题：如何生成训练数据？ 一个经典方法是使用历史观测来预测下一个未来观测。 显然，我们并不指望时间会停滞不前。 然而，一个常见的假设是虽然特定值可能会改变， 但是序列本身的动力学不会改变。 这样的假设是合理的，因为新的动力学一定受新的数据影响， 而我们不可能用目前所掌握的数据来预测新的动力学。 统计学家称不变的动力学为静止的（stationary）。 因此，整个序列的估计值都将通过以下的方式获得：
(8.1.2)¶
注意，如果我们处理的是离散的对象（如单词）， 而不是连续的数字，则上述的考虑仍然有效。 唯一的差别是，对于离散的对象， 我们需要使用分类器而不是回归模型来估计
。”