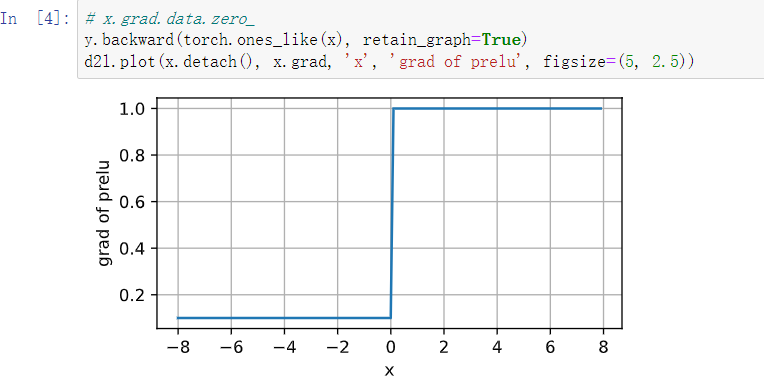
1、x<0, ∂, x>0 1
2、忽略偏置,很好证,加上偏置就是进行平移
3、带入公式即可
4、直接使用非线性单元,如relu,部分数据会被忽略,丧失部分学习能力。
他说的对,直接把这一行注释掉就可以了,没啥用
第二题的完整解法应该是这样的:
简略解释:
- 单个RELU函数是连续的分段线性函数。
- 多个RELU函数的组合(加减)和softmax操作仍然是连续的分段线性函数
- 多层的多个RELU函数的集合虽然函数维度发生变化,但仍然是连续的分段线性函数
通过问题2的延伸学习可得到如下结论:
(证明很复杂,欢迎大神补充通俗易懂的证明过程)
-
含有非线性激活函数的多层感知机在有限空间内能逼近任意连续函数
数学证明:
Multilayer Feedforward Networks are Universal Approximators
Approximation by Superpositions of a Sigmoidal Function -
第二题的结论反过来也成立,任意一个连续的分段线性函数可以被使用ReLU(或pReLU)的多层感知机近似
UNDERSTANDING DEEP NEURAL NETWORKS WITH RECTIFIED LINEAR UNITS的 (Theorem 2.1.)
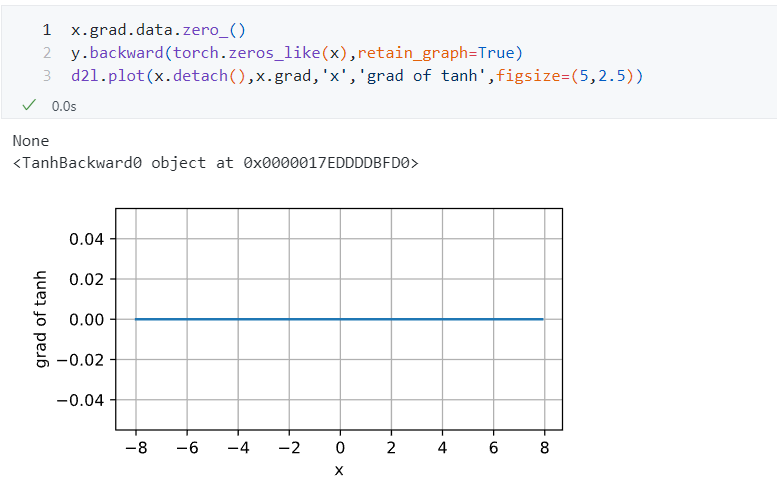
你第一行把梯度设置为了0,这是有问题的,去掉就行了,具体原因我想看看你的x是怎么设置的
4.小批量数据可能不足以捕获整个数据分布的代表性特征,因此梯度估计不稳定
小批量数据可能学习效果差,导致结果看起来还是线性单元?
你好, 据我所知
首先在MLP比较简单的时候, 你可以去检查对某个特征的权重大小
在神经网络比较复杂的时候(包括更复杂的模型), 人们把模型视为一个黑盒而去考虑具体特征对输出有什么贡献, 这一问题对应于深度学习的可解释性这一领域, 具体比较简单的方法有’leave one out’, ‘shap’ 等, 具体可以查看相关资料, 这里简单介绍leave one out的想法
把每个特征一个一个地mask掉, 看输出的改变, 对于mask后导致输出改变更大的特征, 认为它的贡献比较大
希望这些内容能够帮助到你
4.1.1.1中第三段的猫狗识别例子没有很理解到,尤其是这句”在一个倒置图像后依然保留类别的世界里“。有没有大佬可以帮忙继续解释一下。
对图片进行裁剪、旋转、翻转、去色、反向、重取样、调整对比度、曝光度等操作,尽管单个像素的强度和值都发生了改变,照片里的倒着的猫还是一只猫,说明一张图片的内容是猫还是狗和单个像素的强度是没有直接关系的。
但是为什么前面章节有多处直接用==比较的?按一般通用编程的做法不是应该|a - b| < epsilon么?我一直对此很有疑问
忽略数据的问题感觉只有ReLU有吧,那sigmoid、tanh和leaky-ReLU呢?
这段话翻译得不好所以不好理解,实际意思是:在将图像旋转或倒置,输出的类别仍然保持不变的情况下。
通俗的说,就是把猫的照片倒置后,仍然要识别出猫这一类别。对应着前面增加某一位置的单独像素点的强度,是否总是会增加或降低图像的类别似然。
这版翻译的太垃了,很多句子都不通。还不如第一版通顺