此处的loss应该是乘了10 因为计算的时候是对单个batch的数据在计算而不是对整个数据集数据进行计算
练习一
将损失函数的定义方式中的reduction字段改为 'sum'的话,会使得梯度值放大为原来的num_example倍
使得在不改变学习率的情况下 很容易出现在最优解附近震荡的情况 降低学习效果
- 将损失函数的计算方式定义为整个损失的和
loss = nn.MSELoss(reduction='sum')
trainer = torch.optim.SGD(net.parameters(), lr=0.03) #指定需要优化的参数 还有学习率
num_epochs = 3
for epoch in range(num_epochs):
for X, y in data_iter:
l = loss(net(X) ,y) #这里的net返回输入x经过定义的网络所计算出的值
trainer.zero_grad() #清除上一次的梯度值 避免叠加上下面的数据所带来的梯度
l.backward() #损失函数进行反向传播 求参数的梯度
trainer.step() #trainer步进 根据指定的优化算法进行参数的寻优
l = loss(net(features), labels) #根据上面的参数优化结果计算参数对整个数据集的拟合状态 以loss进行反映
print(f'epoch {epoch + 1}, loss {l:f}')
- 在上述情况下改变学习率
trainer = torch.optim.SGD(net.parameters(), lr=0.03/10) #指定需要优化的参数 还有学习率
num_epochs = 3
for epoch in range(num_epochs):
for X, y in data_iter:
l = loss(net(X), y) #这里的net返回输入x经过定义的网络所计算出的值
trainer.zero_grad() #清除上一次的梯度值 避免叠加上下面的数据所带来的梯度
l.backward() #损失函数进行反向传播 求参数的梯度
trainer.step() #trainer步进 根据指定的优化算法进行参数的寻优
l = loss(net(features), labels) #根据上面的参数优化结果计算参数对整个数据集的拟合状态 以loss进行反映
print(f'epoch {epoch + 1}, loss {l:f}')
总结
明显可见地选用sum而不是mean将很大程度影响模型的学习效果
原因:若不将损失函数采用均值 将会使得参数的梯度过大
梯度经过放大后 原有的学习率显得过大 使得其出现了振荡 即步长过长导致
在最优解的附近震荡 而无法高效逼近最优点
-
以平均值作为损失函数
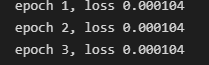
-
以和作为损失函数,不改变学习率
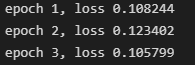
-
以和作为损失函数,改变学习率
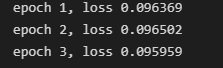
总结:默认情况下以mean作为损失的计算结果更好
个人理解是步进的意思,也就是进行一次优化
我认为在这里的l并不参与梯度优化也就是SGD的循环,所以就算不抹除计算图也没有问题,这一点包括从0实现的代码也是,但是使用了也有一个好处,就是在计算的时候不需要包含梯度信息,所以可以显著的减少内存开销。
学习率除以10是保证了优化时梯度和原来相比保持不变
但是这里epoch算的是所有样本的损失,就会相比原来大1000左右
1000个样本按batch_size=10划分,分成了100份,迭代一次样本需要100次sgd优化,我猜这个trainer.step()就是每循环一次执行一个batch_size的sgd优化
自己从零实现的损失函数和调库实现的不同,改成(y_hat - y.reshape(y_hat.shape)) ** 2就一样了
请问在运行100遍next(tier(data_iter))后,还是会有输出,是从头开始了吗
不知道有没有人做了第二题,去查了一下pytorch的文档,发现提供的是 [nn.MSELoss], [nn.NLLLoss], [nn.CrossEntropyLoss]这几种损失函数,想试图自己写一个Huber_loss的函数,但是矩阵中每个元素和delta比较的结果不同,这样的话使用不同的loss就需要遍历整个tensor,不知道有什么好的解决办法吗?
计算完损失函数会进行反向传播计算梯度,梯度计算完之后调用优化器进行梯度更新
Pytorch是有提供nn.HuberLoss的哦,你再看看
Thanks。What you said is really good
大家好,我按照本节的代码构建了线性回归模型,在cpu上训练时完全没有问题,但使用gpu的时候就报错:CUDA error: CUBLAS_STATUS_INVALID_VALUE when calling cublasSgemm( handle, opa, opb, m, n, k, &alpha, a, lda, b, ldb, &beta, c, ldc)
我查了许多网页,大部分情况都是因为nn.Linear的dimension与输入不一致导致的。但在我的例子中cpu可以跑通说明不是这个问题。我还怀疑过是显存不足,但使用极小的数据集同样报错。
想知道有没有人遇到跟我一样的问题,并请教如何解决,谢谢!
The problem have been posted to python - Pytorch CUDA error: CUBLAS_STATUS_INVALID_VALUE when calling `cublasSgemm( handle, opa, opb, m, n, k, &alpha, a, lda, b, ldb, &beta, c, ldc)` - Stack Overflow
Any suggestion is appreciated!
因为框架里面的MSELoss()默认返回的是一个batch的平均损失,是已经求和并求平均了的,因此不需要再求和。
第一题中
-
nn.MSELoss(reduction='sum'): 当设置reduction='sum'时,损失函数将计算预测值与目标值之间的平方差,并对所有平方差求和。这意味着你会得到一个单一值,表示所有样本的总损失。 -
nn.MSELoss()(默认reduction='mean'):当没有指定reduction参数或将其设置为'mean'时,损失函数将计算预测值与目标值之间的平方差,并对所有平方差求平均。这意味着你会得到一个单一值,表示所有样本的平均损失。
实际上我们可以得出:nn.MSELoss()=nn.MSELoss(reduction='sum')/batch_size
因此,当我们用nn.MSELoss(reduction=‘sum’)替代nn.MSELoss()时,只需要对lr除以batch_size就行。因为在求导过程中,常数项作为系数保持不变,梯度的大小也乘上了batch_size
练习2
def Huber(pred , true , sigma = 0.005):
error = abs(pred.detach().numpy() - true.detach().numpy())
return torch.tensor(np.where(error < sigma , error - sigma / 2 , 0.5 * sigma * error ** 2) , requires_grad= True).mean()
我觉得可能是因为从零开始的那个公式里我们为了后面求完导得出来简洁的公式,因此当时乘以了二分之一(因为这个推导过程是我们手算的,而pytorch实现不需要乘以二分之一,因为求导不需要人来求,也不需要你看到简洁的公式)
练习2
def huber_loss(y_hat, y, beta = 0.005):
error = torch.abs(y_hat - y.detach())
return torch.where(error < beta , 0.5 * error ** 2 / beta, error - 0.5 * beta)
nn.MSELoss() 优于 nn.MSELoss(mean)
默认是什么??
练习2
def Huber(y_hat,y,sigma) :#@save
loss_temp=nn.L1Loss()
loss=loss_temp(y_hat,y)
flag=loss-sigma
if flag>0:
return loss-sigma/2
else:
return 1/(2*sigma)*loss**2