https://zh.d2l.ai/chapter_linear-networks/linear-regression-scratch.html
有个疑问,SGD方法的batchsize参数,是不是不需要作为参数传入,而是在方法内部计算为佳?
从后面简洁实现来看,sgd的时候似乎也并不需要传入batchsize参数
看代码实现
这一段
dw, db = g.gradient(l, [w, b])
# 使用参数的梯度更新参数
sgd([w, b], [dw, db], lr, batch_size)
dw,db并没有计算batch_size,就是计算的顺序变了
Exercise 1
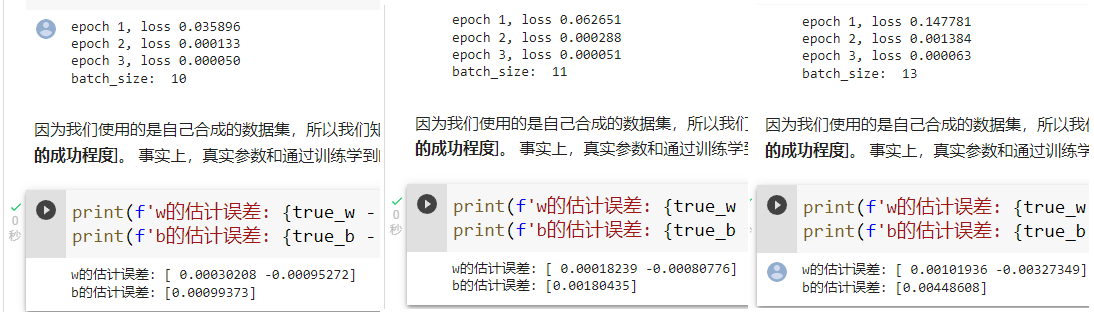
初始化为 0 跑了几遍,仍然能够得到有效的结果。所以算法仍然是有效的。
Exercise 2
可以的,先假设电压和电流的关系为 U = wI + b,然后找到 (U, I) 的数据集,然后跑一遍这个模型。
Exercise 4
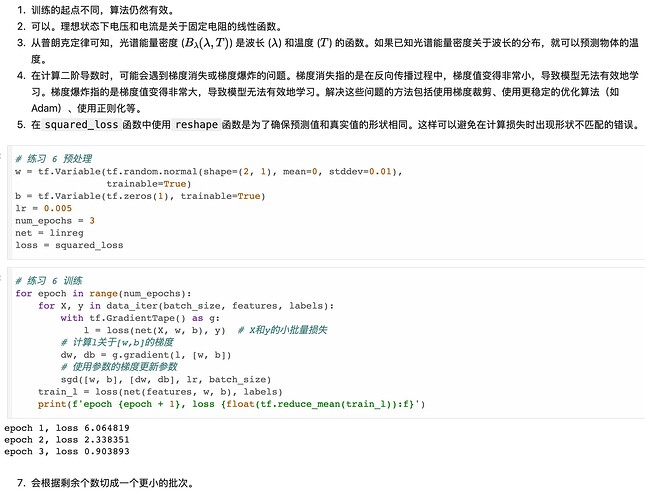
在计算二阶导的时候需要一阶导的结果。需要保存一阶导的结果。
Exercise 5
为了保证 y 和 y_hat 的形状一样,避免出现一个是行向量一个是列向量的情况。
Exercise 7
data_iter 最后取出来的一组数据没有 batch_size 个,但是计算 sgd 的时候仍然除了 batch_size,结果应该不会很准确,误差会比能整除的要大一些。
batchsize通常是自己设定的,这个参数属于超参数,他的设置涉及到模型和你的设备影响
在更多更大更复杂的模型下参数需要用户自己慢慢调
在这个代码示例中,损失函数被定义为
def squared_loss(y_hat, y):
"""均方损失"""
return (y_hat - tf.reshape(y, y_hat.shape)) ** 2 / 2
这里的注释“均方损失”感觉有点误导,它只是对每个真实值 y 和预测值 y_hat 计算了平方误差,其结果是和 y 形状相同的向量。
平方误差的求和发生在 g.gradient(l, [w, b]) 的地方,这里因为 targets(第一参数)是向量有多个标量值,g.gradient 会计算所有 targets 的和的偏导数(也是每个 target 对 w 或 b 的偏导数的和,因为 d(y+z) / dx = dy/dx + dz/dx)。所以 dw, db 里的值是所有样本平方误差的对应偏导数的和。
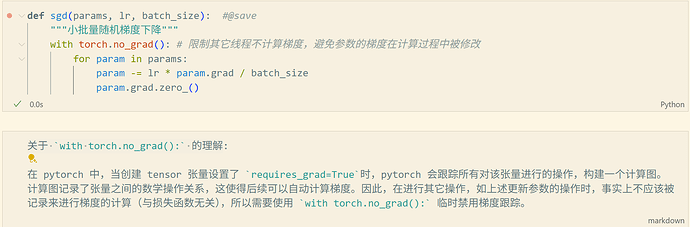
然后在 sgd 方法里面,grad / batch_size 才把和除以样本数量,得到平均值,也就是真正的梯度 g,乘上学习率 lr 得到应当从参数中减去的量。
所以这里的梯度计算被分到三个地方:
- 损失函数 squared_loss 求平方误差,得到 batch_size 维的平方误差向量。这个计算过程被 GradientTape 记录用来计算后面的偏导数。
- g.gradient 求偏导数,并求和
- sgd 把和除以 batch_size 最终得到前面公式中是梯度 g