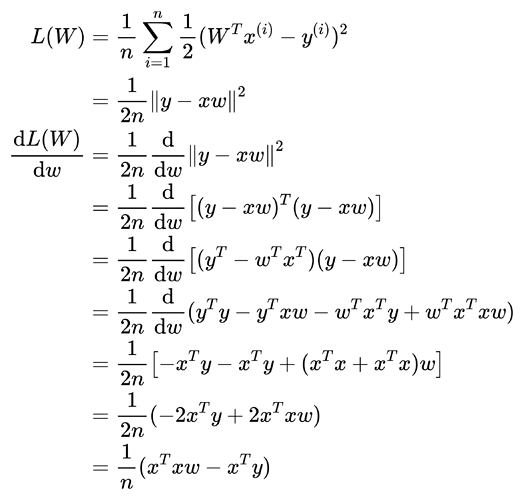https://zh.d2l.ai/chapter_linear-networks/linear-regression.html
如果确定x遵循正态分布N(μ, σ²),则b=mean(x)是μ的极大似然估计量
3.1.3.讲的是,假设样本特征的数值由两部分组成,其中一部分完全符合线性模型,另一部分完全是符合正态分布的噪声,则平方损失目标函数可以期望排除正态分布的噪声,从而收敛到隐含的实际线性模型。
这个人写了推导过程,最后算出来应该是要把各样本点预测值和实际值之误差的绝对值之和
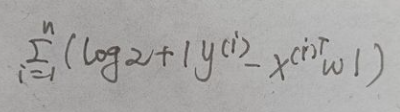
最小化,像他说的绝对值和不能最小化改求平方和,感觉目标都变了,我甚至觉得他提出来的问题不一定是作者想让我们考虑的问题,但到底是啥我还没想到。。。
因为是绝对值式的和,有些点确实是不可导,但是应该很难取到这些点,而且如果取到了,把两边导数相加除以二就行了。哦,大概作者说的问题就是这个了吧。
至于可能会有局部最小值,梯度下降不能保证得到全局最优解,这就属于 3.1.1.4.最后一段说暂时不考虑的了吧。
问题1.1
最小均方差估计在几何上等价于用一定维度的向量去估计目标向量,最小均方差误差估计为目标向量在维度(线、平面、超平面)上的投影。
以常数b估计,等价于以一维向量Y^={b,b,b,…,b}去估计向量Y={x1, x2, … xn}T,等价于向量-向量的投影问题,求Y在向量X ={1,1,1,…,1}上的投影Y^,投影矩阵P=XXT/(XTX),可得Y^=PY,可求得b为xi的均值(P为元素全为1/b的矩阵)
Exercise 1

Exercise 2
主要使用2.4.3. 梯度中的知识:
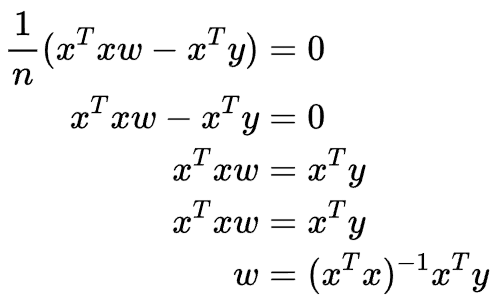
当为凸函数时(只有一个最优解),使用这种方法比使用随机梯度下降要好,而在损失函数不是凸函数,存在多个局部最优解时,这时我们可能无法找到解析解,这种方法就会失效。
3.3中,个人觉得可能是在驻点得到的是局部最优值而不是全局最优