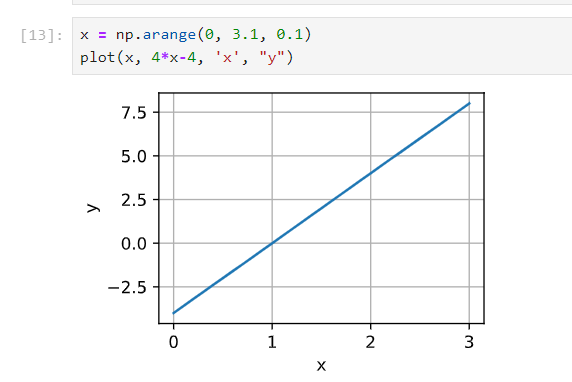
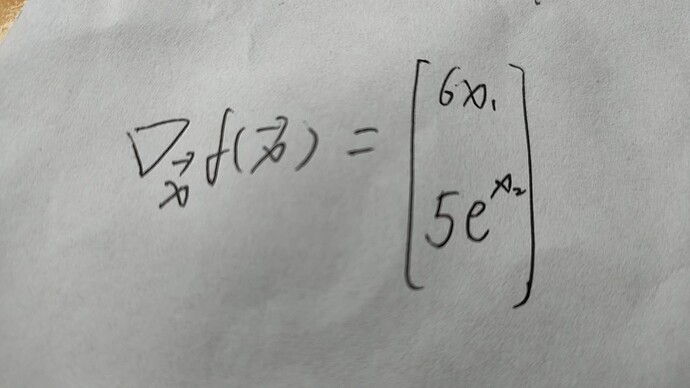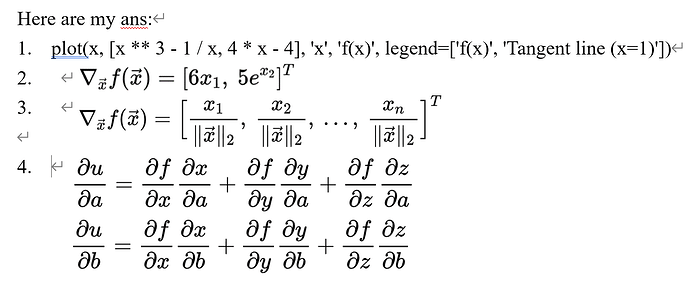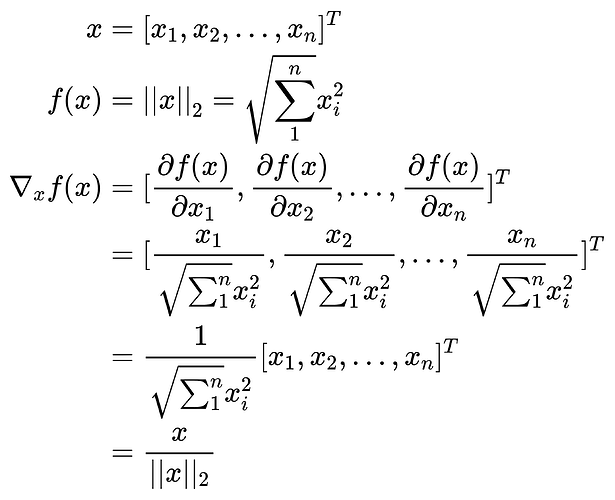x = np.arange(0, 3, 0.1)
plot(x, [x3 - 1/x, 3*x2 + 1/(x**2)], ‘x’, ‘f(x)’, legend=[‘f(x)’, ‘Tangent line (x=1)’])
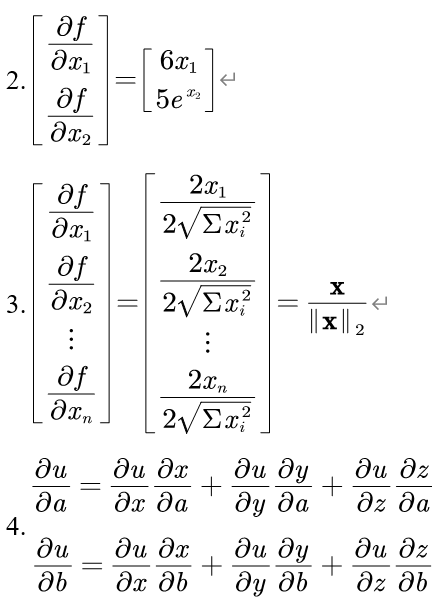
[6x_1, 5e^{x_2}]
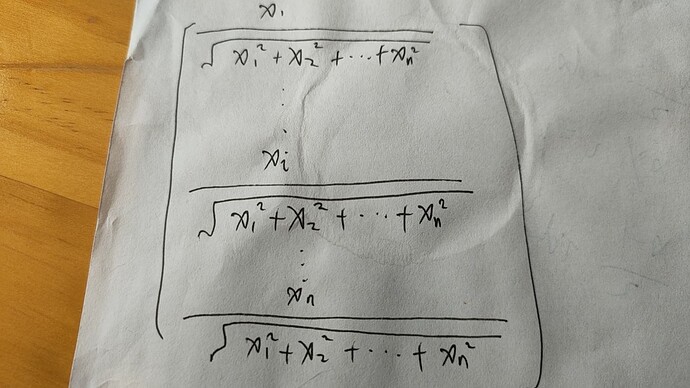
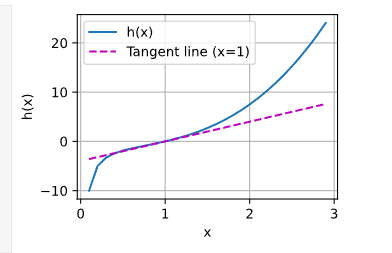
[x_1/||x||, x_2/||x||,…]
du/da = du/dx*dx/da…
赞同，想问下你们都用什么来编辑数学符号，latex？
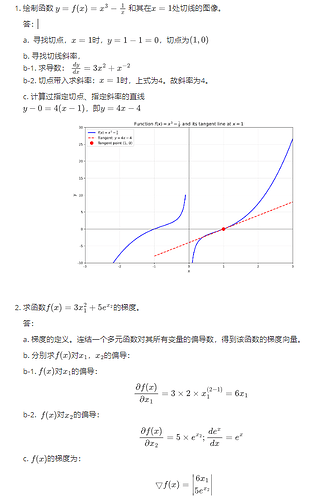
第一题：
先求得导函数f’(x)=3x^2+1/(x^2)
当x=1时，切线就是y=4x-4
https://zh.d2l.ai/chapter_preliminaries/calculus.html#subsec-calculus-grad
这里的运算规则给我看迷糊了，为啥Ax的梯度是A转置?
# hw 1
def f(x):
return x ** 3 - 1 / x
plot(x, [f(x), 4 * x - 4], 'x', 'f(x)', legend=['f(x)', 'Tangent line (x=1)'])
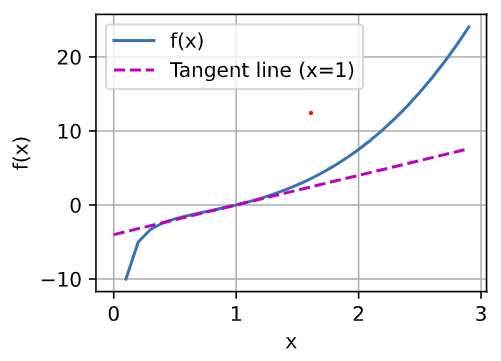
其实应该是 2.3 * x - 3.3 ，用 2 * x - 3 在图形界面上看不出区别，所以问题不大。
2.3 是 1.0 位置的斜率，(y2 - y1) / (x2 - x1) 可以得到
-3.3 是为了在 1.0 这个 x 点重合，调整 y 的值
具体可以看下边的注释
x = np.arange(0, 3, 0.1)
y = f(x)
print(x)
x1 = x[10]
x2 = x[11]
y1 = f(x1)
y2 = f(x2)
print(f'x1={x1}') # 取 x = 1.0 这个点
print(f'f(x1)={f(x1)}') # x = 1.0 时，y = -1.0
print(f'(y2 - y1) / (x2 - x1)={(y2 - y1) / (x2 - x1)}') # 差值是 0.1 的时候求斜率，是 2.3，如差值为 0.00001 无穷小，则斜率无限趋近于为 2，所以用 2 也没错
print(f'y1 - (2.3 * x) = {y1 - (2.3 * x1)} ') # 让斜率这条线和曲线在 x=1.0 点重合，看 y 要怎么调整，得到 y 要 - 3.3
plot(x, [y, 2.3 * x - 3.3], 'x', 'f(x)', legend=['f(x)', '2 * x - 3'])
主要是需要理解这里的f(x)=||x||^2中的x是一个n维向量( x=[x1,x2,…,xn] )，||x||是x的欧几里得范数（线性代数），||x||^2就是x各个分量的平方和。即
f(x)=||x||^2，将向量x展开来写，形式就是：
f(x1,x2,…,xn)=x1^2+x2^2+…+xn^2。
x=[x1,x2,…xn]作为输入，它的每个分量都是一个变量，f(x)本质是n元2次函数，f(x)的梯度，就是f(x1,x2,…xn)分别对x1,x2,…xn求偏导（高数）得到的结果组成的向量，即
[2*x1,2*x2,…,2*xn)，写成向量的形式就是
f(x)=||x||^2的梯度是2x