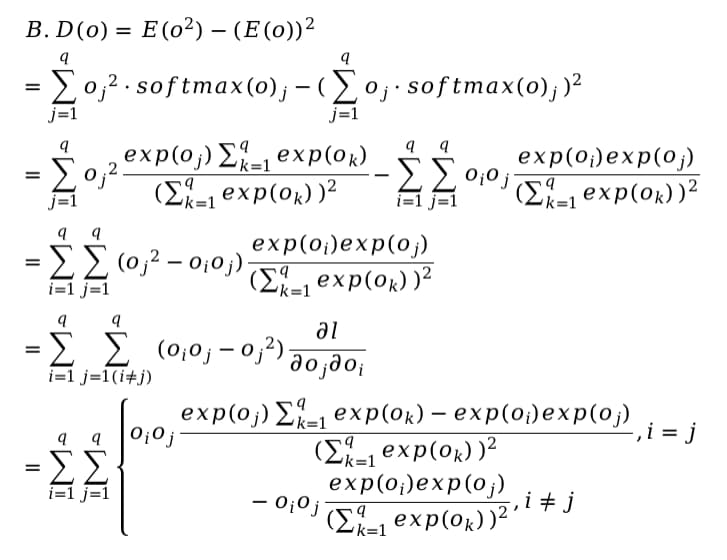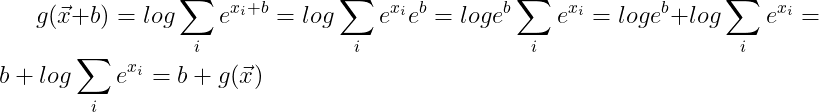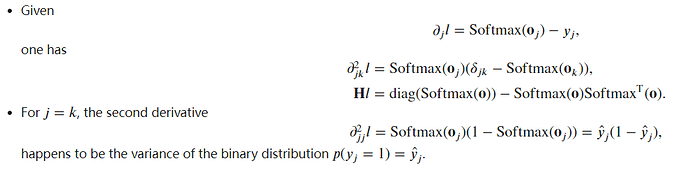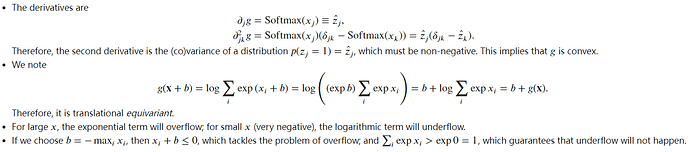Any further reading suggestion for question 7?
Here are my opinions for the exs:
I still not sure about ex.1, ex.5.E, ex.5.F, ex.6
ex.1
But, what does “match” means in question B?
ex.2
A. If I use binary code for the three class, like 00, 01, 11, then the distance between 00 and 01 is smaller than that between 00 and 11, that is oppose to the fact that the three class is of equal probability.
B. I think I should use one-hot coding mentioned in this chapter, because for any independent observation(which I think is a class), there contains no distance information between any pair of them.
ex.3
Two ternaries can have 9 different representation, so my answer is 2.
This ternary is suitable for electronics because in a physical wire, there will be three distinctive condition: positive voltage, negative voltage, zero voltage.
ex.4
A. Bradley-Terry model is like
When there are only two classes, softmax just fit this.
B. No matter how many classes there will be, if I put a higher score for class A compared to class B, the the B-T model will still let me chose class A, and after 3 times of comparing, I will chose the class with the highest score, that still holds true for the softmax.
ex.5
ex.6
This is my procedure for question A, but I can’t prove that the second derivative is just the variance.
As for the rest of the questions, I don’t even understand the question.
ex.7
A. Because of exp(−𝐸/𝑘𝑇), if I double T, alpha will go to 1/2, and if I halve it, alpha will go to 2, so T and alpha goes in opposite direction.
B. If T converge to 0, the possibility for any class will converge to 0, and the proportion between two class i and j exp( -(Ei - Ej) /kT) will also converge to 0. Like a frozen object of which all molecules is static.
C. If T converge to ∞, the proportion between two class i and j will converge to 1, which means every class has the same possibility to show up.
1 Like
Exercise 6 Show that g(x) is translation invariant, i.e., g(x+b) = g(x)
I don’t see how this can be true for b different from 0.
1 Like
Ex1.
Ex6 (issue: (1) translational invariant or equivariant? (Softmax is invariant, but log-sum-exp should be equivariant); (2) b or negative b? Adding maximum can make overflow problem worse).
The same result… I think we may say the log-partition function is translational equivariant rather than invariant. See also this page.
To ex.1, maybe we can take softmax distribution as Bernoulli distribution with a probability of $p = softmax(o)$, so the variance is:
$$Var[X] = E[X^2] - E[X]^2 = \text{softmax}(o)(1 - \text{softmax}(o))$$
I don’t know whether this suppose is right
and my solutions to the exs: 4.1
Does this mean that each coordinate of each y label vector is independent of each other? Also, shouldn’t the y_j of the last 2 equations also have a “i” superscript?
I read the URL given, but it doesn’t clarify too much for this specific case.
could this equation be generalized if $\textbf{y^{i}}$ was not one-hot encoded vector but a soft label or a probability distribution?
I think here should be the author wanted to express.
P=\prod{ P(\vec{y}{i}|\vec{x} {i}) }
\vec{x}{i} is the i th image, is the a 4X1 vector in case of a 2x2 image
\vec{y} {i} is the softmax result, is a 3X1 vector in case of 3 different classification results.
The P means we must max the accuracy of all the n image classification results, not only a single image. Am I correct?
how ever, the result P should be a 3X1 vector eventually.
The superscript $i$ indicates the i-th data sample and its corresponding label. And in the context of image classification here, yes, $\textbf{x}^{(i)}$ is the pixel tensor that represents the i-th image, $\textbf{y}^{(i)}$ is the category vector of this image.
What I asked is that if or not this equation could be applied to a general case, namely $\textbf{y}^{(i)}$ is not a one-hot encoded vector but a vector presents possibilities for each category. In my understanding after reading section 22.7, the answer is no.