Softmax Regression Implementation from Scratch

[mli]

https://d2l.ai/chapter_linear-classification/softmax-regression-scratch.html

[gpk2000]

The cross entropy loss is given by the below formula according to this

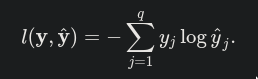
But in the code below is the same thing happening?

def cross_entropy(y_hat, y):
    return - np.log(y_hat[range(len(y_hat)), y])

Am I missing something?

[StevenJokes]

@gpk2000
You can test by your own next time…
Just try to input some numbers to see the outputs…

---

And use the search button as possible.

http://preview.d2l.ai/d2l-en/master/chapter_appendix-mathematics-for-deep-learning/information-theory.html?highlight=cross%20entropy%20loss

---

.mean() is for n*1 matrix?
@goldpiggy

[osamaGkhafagy]

What this snippet of code is doing is exactly the same as the formula above. This code uses the index of the true y to fetch the predicted value y_hat and then taking the log to those predicted values for all examples in a minibatch

[katduecker]

I am also a bit confused about that. I get that we select the y_hat for each y, in train_epoch_ch3 we sum over the cross-entropy loss, but where do we multiply each y with it’s corresponding y_hat as per the equation?

[goldpiggy]

Hi @katduecker, great question! I guess you were referring to the “loss” function. Here we usedcross entropy loss rather than simply multiplying y and y_hat in the function cross_entropy.

[Nisar_Khan]

Hi,
I think there is a typo in the sentence : “Before looking at the code, let us recall how this looks expressed as an equation:”
It should be : “Before looking at the code, let us recall how this looks when expressed as an equation:”
Thank you.
Nisar

[gudzpoz]

I might be able to explain the derivation of the cross_entropy function a little bit.
Indeed, 𝓁(y,ŷ)=-Σy_j log(ŷ_j).
However, we see that y is in reality (0, … 0, 1, 0, …, 0) so we have:
𝓁(y,ŷ)=-Σy_j log(ŷ_j)=-y_i log(ŷ_i), where y_i=1,
as all other terms are just zero.
Since y_i=1, we can further simplify this into:
𝓁(y,ŷ)=-y_i log(ŷ_i)=-log(ŷ_i), where y_i=1.

def cross_entropy(y_hat, y):
    return - np.log(y_hat[range(len(y_hat)), y])

In the code, y is (i⁽¹⁾, i⁽²⁾, …, i⁽ⁿ⁾)
and y_hat[range(len(y_hat)), y] is just (ŷ⁽¹⁾_i⁽¹⁾, ŷ⁽²⁾_i⁽²⁾, …, ŷ⁽ⁿ⁾_i⁽ⁿ⁾)
with -np.log getting the logarithm of them all at once.

[MrBean]

softmax的一个稍微好一点的实现

import torch
def crossEntropyNaive(x):
    expX = torch.exp(x)
    return expX / expX.sum(axis = 1, keepdim=True)

def crossEntropySlightlySmart(x):
    row_max,_ = torch.max(X, dim = 1, keepdim=True)
    x = x - row_max
    expX = torch.exp(x)
    return expX / expX.sum(axis = 1, keepdim=True)


X = torch.tensor([[1.0,1.0],[1.0,10.0],[1.0,100.0]])
print(crossEntropyNaive(X))
print(crossEntropySlightlySmart(X))