Maybe it is just a coincidence that almost 90 groups of experiments is “die = 6”?
It would be more clear if you counts / 1000 # Relative frequency as the estimate.
In L2/5 Naive Bayes, in terms of Nvidia Turing GPUs, why Alex said adding more silicons is almost free for Nvidia?
Hi @ness001, great question! Check here for more details about GPUs 13.4. Hardware — Dive into Deep Learning 1.0.3 documentation
for question #3 can we calculate it like this :
P(A,B,C) = P(A/B,C) * P(B,C) and as B not depend on c
P(A,B,C) = P(A/B,C)*P(B)*P©
is it correct like this or not ? if not could you please explain why?
thanks in davaned
For Q4:
If we do the test 1 twice, the two tests won’t be independent, since they are using the same method on the same patient. In fact, we will get the same result very possibly.
For Q3
P(ABC)=P(C|AB)P(AB)=P(C|B)P(B|A)P(A)
is it right? is it the simplest answer for Q3?
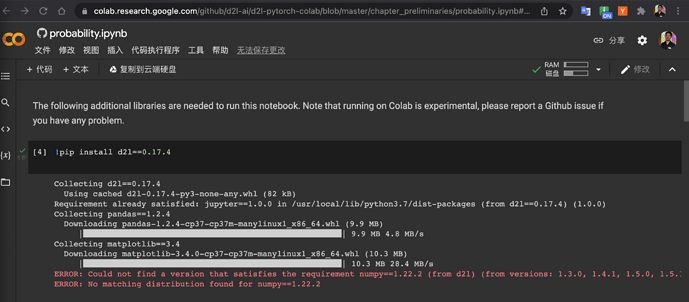
Can you try !pip install d2l, I succeeded, and where did you get this 0.17.4 version?
It does work. I use pytorch in colab. Thank you so much.
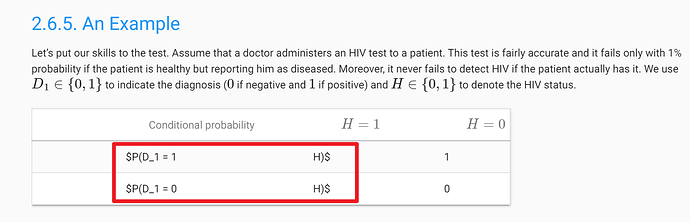
In section 2.6.2.6
P(D1=1,D2=1) = P(D1=1,D2=1|H=0) * P(H=0) + P(D1=1,D2=1|H=1) * P(H=1)
Is this equivalent to (since D1 and D2 are independent)
P(D1=1,D2=1) = P(D1=1) * P(D2=1) ?
P(D1=1) has been calculated in equation 2.6.3 and P(D2=1) can be calculated similarly.
I am having a hard time proving this. Am I missing something?
“…by assuming the conditional independence”
my bad.
Maybe there’s a typo in 2.6.7 which should be 0.00176655 and I have 0.8321304237 in 2.6.8. Correct?
For the last question
If we assume the test result is deterministic, then
P(D2=1|D1=1) = 1
P(D2=0|D1=0) = 1
Doing first experiment twice does not add additional information. Therefore, P(H=1|D1=1,D2=1) == P(H=1|D1=1). You can derive the equation by doing some arithmetic.
I don’t understand equation 2.6.3 . On the right side, why wouldn’t P(A) on the top cancel out with P(A) on the bottom, and since the other term on the bottom right which is the sum of all b in B for P(B|A) equals 1, wouldn’t that mean it would then just simplify to P(A|B) = P(B|A) which is obviously incorrect?
Yes, the equation is slightly wrong. The updated equation should sum over all possible ‘a’ values in the sample space(a and its complement so that it gets normalized accurately), Reference
An error in exercise 4? It says we draw n samples and then uses m in the definition of zm.
Would have been great and more clear to actually see what numbers you multiplied in the example, for someone never doing stats before, it can be hard to comprehend all the formulas without any explanations.
Answer for Problem 7:
Part 1:
| P(D2=1|H=0) | P(D2=0|H=0) | Total
P(D1=1|H=0) | 0.02 | 0.08 | 0.10
P(D1=0|H=0) | 0.08 | 0.82 | 0.90
Total | 0.10 | 0.90 | 1.00
Part 2:
P(H=1|D1=1) = P(D1=1|H=1) * P(D2=0|H=1) / P(D1=1)
P(D1=1) = P(D1=1,H=0) + P(D1=1, H=1)
=> P(D1=1) = P(D1=1|H=0) * P(H=0) + P(D1=1|H=1) * P(H=1)
Thus, P(H=1|D1=1) = (0.99 * 0.0015) / ((0.10 * 0.9985) + (0.99 * 0.0015)) = 0.01465
Part 3:
P(H=1|D1=1,D2=1) = P(D1=1,D2=1|H=1) * P(H=1) / P(D1=1,D2=1) (1)
P(D1=1,D2=1|H=1) = P(D1=1|H=1) * P(D2=1|H=1) (2)
P(D1=1,D2=1) = P(D1=1,D2=1,H=0) + P(D1=1,D2=1,H=1)
= P(D1=1,D2=1|H=0) * P(H=0) + P(D1=1,D2=1|H=1) * P(H=1) (3)
Using (1), (2), & (3),
P(H=1|D1=1,D2=1) = 0.99 * 0.99 * 0.0015 / (0.02 * 09985 + 0.99 * 0.99 * 0.0015) = 0.06857
Are the above answers correct??